Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Брянский государственный университет им. академика И.Г. Петровского

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

pan1327

.pdf

Скачиваний:

Добавлен:

30.05.2015

Размер:

2.03 Mб

Скачать

☆

1 / 21 2 > Следующая >>>

Московский авиационный институт (национальный исследовательский университет) ЭЛЕКТРОННЫЙ ЖУРНАЛ

www.mai.ru/~apg «ПРИКЛАДНАЯ ГЕОМЕТРИЯ» Выпуск 13, N 27 (2011), стр. 1-11

РЕКОНСТРУКТИВНАЯ ГЕОМЕТРИЯ КРИВОЙ ЛИНИИ

Д. С. Корчагин, К. Л. Панчук ГОУ ВПО «Омский государственный технический университет»

644050, Омск, Пр. Мира, д. 11.

E-mail: Korch-Den@yandex.ru, Panchuk_KL@mail.ru.

Аннотация. В статье рассматривается взаимосвязь дифференциально-

геометрических характеристик кривой линии и ее проекций, позволяющая восстанавливать кривизну и кручение кривой линии пространства по ее ортогональным проекциям.

Ключевые слова: пространственная кривая линия, проекции, кривизна, кручение,

направляющие косинусы, трехгранник Френе, винтовая линия.

СОДЕРЖАНИЕ Аннотация…………….…………………………………………………………………1

Введение……………………………….…………………………………………….......1

1.Определение кривизны и кручения кривой линии по ее ортогональным проекциям……………………………….……………………………………………….2

2.Пример восстановления кривизны и кручения цилиндрической винтовой линии по ее проекциям…………………….…………………………..……………………….7

Заключение……………...……………………………………………………………..11

Список использованных источников…………………..………………………….....11

Введение

В задачах геометрического моделирования пространственной кривой линии возникает необходимость оперирования с ее инвариантами – кривизной и кручением. В работе предлагается расчетный алгоритм восстановления кривизны [1]

и кручения пространственной кривой линии по ее проекциям.

(с) МАИ, 1999-2011

2 Корчагин Д.С., Панчук К.Л./ Прикладная геометрия, вып 13, № 27 стр. 1-11

1. Определение кривизны и кручения кривой линии по ее ортогональным проекциям

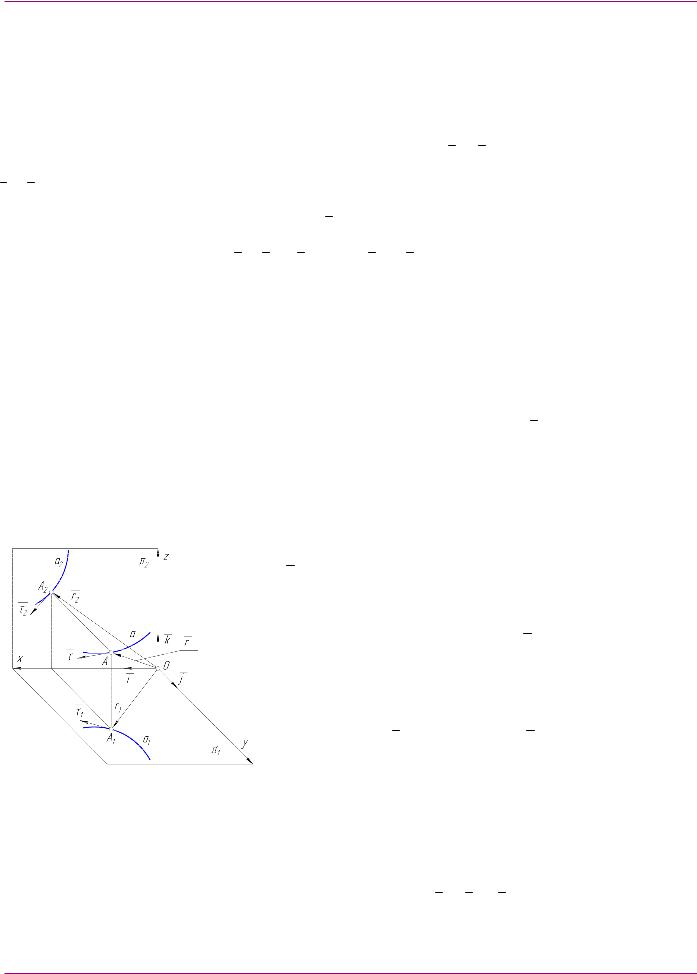
Рассмотрим пространственную кривую a, заданную своими ортогональными

проекциям a1 и a2 на плоскостях проекций π1 и π2, соответственно (рис.1). Пусть эти проекции описываются векторными уравнениями: r1 r1(s1), где s01 s1 sn1;

r2 r2(s2), где s02 s2 sn2. Тогда на основании проекционной схемы (рис. 1) имеем зависимости для радиус-вектора кривой r :

r1 (

r2 k)k

r2 (

r1 j) j,

(1)

что позволяет определить единичный касательный вектор искомой кривой a в

пространстве

dr1

ds1

dr2

ds2

ds1

ds2

k( 2 k)

(2)

а также получить выражение второй производной радиус-вектора

(s)

d2s

r k

ds2

k (

(

k)k

(3)

1 1

ds2

Уравнение (2)

можно

представить в

виде

(r k

)k ,

где

точками,

обозначено

дифференцирование по параметру s. Очевидно,

для

определения

вектора

точке A a c

параметром s, необходимо выполнение для этой

точки хотя бы одного из условий:

dr1

ds1

0; r

dr2

ds2

Рис. 1 Проекционная схема для

каждое, из которых соответствует достаточному

пространственной кривой

признаку

существования

обыкновенных

точек

[2] A1 a1, A2 a2,

проекционно-соответственных точке A a с параметрами s1 и s2

соответственно. Уравнение проекции a1 имеет вид

(

что позволяет

(с) МАИ, 1999-2011

Корчагин Д.С., Панчук К.Л./ Прикладная геометрия, вып 13, № 27 стр. 1-11 3

																	r					dr1
определить производную радиус-вектора												r	:															r2			(
																																k	)k .	На
																																k	)k .	На
											1							1					ds			1		1
основании чего запишем выражение
							r	2 1 (													)2 .													(4)
							r	2 1 (										k			)2 .													(4)
						1
Последнее уравнение на основании (2) можно преобразовать к виду
	r	2 1		(					)	ds2				2.																				(5)
					2	k				ds2
						k
1
											ds
																			2						2		ds		2
																			2						2		ds		2
Учитывая, что имеет место				выражение													r							r				1		, уравнение				(5)
Учитывая, что имеет место				выражение													r							r						, уравнение				(5)
																		1						1			ds
можно записать следующим образом:																											ds
можно записать следующим образом:
ds			2												ds					2
ds			2								k)				ds
		1	1			( 2												2	.															(6)
		ds	1			( 2										ds			.															(6)
		ds														ds

Для кривых a1 и a2, принятых в качестве ортогональных проекций некоторой кривой a пространства, имеют место тождественные равенства


												r1 i									r2 i								r		i .							(7)
Дифференцируя эти равенства по параметру s, получим
	1			ds1					2							ds2
			i	ds1							i					ds2										i		,										(8)
			i	ds							i					ds										i		,										(8)
				ds												ds
откуда следует:
						ds1												ds2							.
						ds1							2		i			ds2																				(9)
																																						(9)
						ds				1 i										ds
Из сравнения уравнений (6) и (9) следует выражение производной
	ds															(							)2												1/2
	ds	2														(	1		i				)2												1/2
		2															1																		.			(10)
	ds											2												2										2


				(			2 k)							( 1 i)												( 2 i)
Последнее уравнение позволяет преобразовать выражение (9) к виду
					ds																			(						)2							1/2
					ds																			(			2	i		)2							1/2
					1																						2										.	(11)
					ds															2												2				2

																						( 1 i)											( 2 i)
								( 2 k)														( 1 i)											( 2 i)

Повторное дифференцирование (11) приводит к выражению второй производной

(с) МАИ, 1999-2011

k A2 B2 C2 1 2,

4 Корчагин Д.С., Панчук К.Л./ Прикладная геометрия, вып 13, № 27 стр. 1-11

					d2s			3 k			2	2 2 k
					1						2				1		,									(12)
					ds2				2 2					2 2			,									(12)

в котором приняты следующие обозначения: 1 i																			;		1 i			;	2 i ;	2 i ;

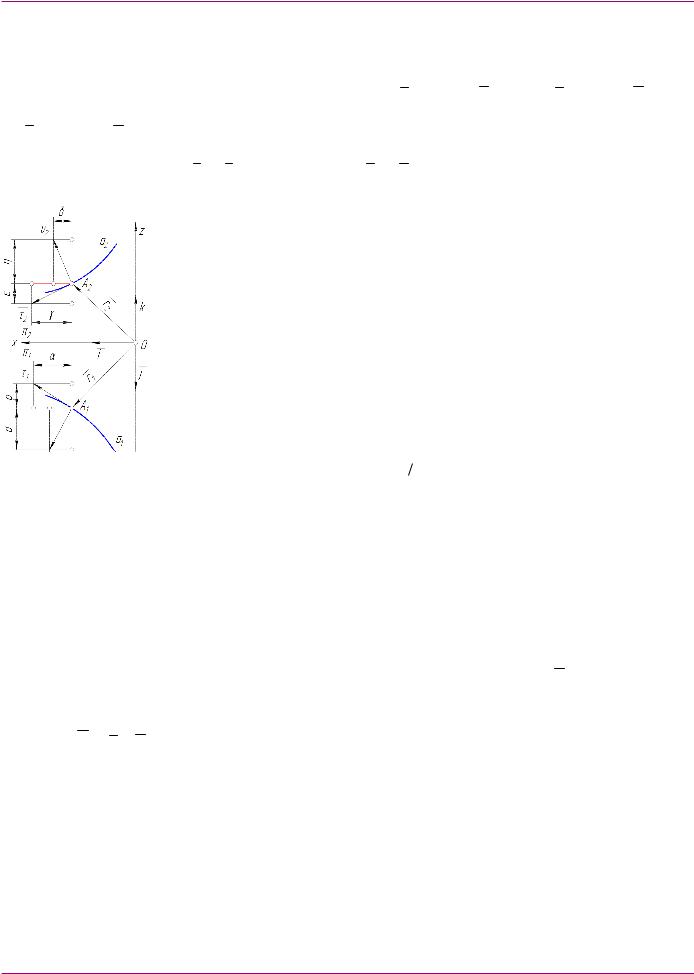
	2 k	;	2 k (где α,		β,		γ,		δ, ε,				η – направляющие косинусы единичных
векторов касательных 1,					2	и			нормалей 1 ,						2			проекций						a1 и a2 кривой a,
				образованные									с	ортами

																			i	,			j, k	базовой		системы
				координат xOyz кривой a (рис.2). Повторное
				дифференцирование выражения (10) также приводит к
				выражению второй производной:
								d2s		2		2 2 k			2	3k
										2					2						1	.				(13)
								ds2						2 2	2 2							.				(13)

Рис.2 Единичные векторы касательных и нормалей проекций кривой

Полученные формулы позволяют выразить из уравнения (3) кривизну k искомой кривой a пространства

(14)

d2s

где

приняты следующие

обозначения: A

ds2

d2s

B k

, C

ds2

Вновь обращаясь к уравнению (3) видим, что оно с учетом выражений (10), (11), (12), (13) позволяет определить в пространстве вектор нормали кривой а, по ее заданным ортогональным проекциям. Это дает возможность из известной

формулы определить вектор бинормали рассматриваемой кривой, а значит и трехгранник Френе, связанный с этой кривой.

Далее перейдем к раскрытию взаимосвязи кручения кривой линии а с ее заданными ортогональным проекциям a1 и a2, для чего выполним дифференцирование выражения (3) по параметру s, в результате чего получим:

(с) МАИ, 1999-2011

Корчагин Д.С., Панчук К.Л./ Прикладная геометрия, вып 13, № 27 стр. 1-11 5

ds 2

ds d2s

d2s

d3s

d2s

k 2

ds ds2

ds2

ds3

ds2

1 1

(15)

d3s

d2s

k k

ds3

ds2

											d 1 ds1															ds1					d 1 ds1												ds1
											d 1 ds1															ds1					d 1 ds1												ds1
где 1																		1k1											; 1											1k1				- производные единичных векторов
где 1												ds			ds			1k1								ds			; 1		ds						ds			1k1			ds	- производные единичных векторов
														1																				1
1	и 1						проекции a1													по длине дуги s пространственной кривой линии а,
								ds1																		;	ds2														;					k2						;			k2		;
								ds1																			ds2																												k2
								ds
								ds							2 2 2													ds		2 2 2														2 2 2									2 2 2
		d3s											ds					2		2		2					2						2											2				2			k		2			2
							1								1						k		2						1					k				k 5 4											k					k
																					k	2	2						1					k		2		k 5 4											k	2				k
			ds3																			2														2			1											2	2			1
			ds3										ds
										1								4 k											k			ds			2			d	2s		1
																																			2				1								;
				α2ε2 γ2 2																																											;
				α2ε2 γ2 2																								2		1 ds ds2 2 2 2
				d3s					2					ds		2	2k k																																		k
									2							2									4 2 1 2k 2 2k																				2 1 2 2								2 k			2
																								2	4 2 1 2k 2 2k																				2 1 2 2								2 k
					ds3																1			2															1					2							2			2
					ds3									ds
													1						4 k2 k2															ds2					d2s2		1
						2 2 2 2													4 k2 k2															ds					ds2			2 2		2

- производные по s, выраженные через направляющие косинусы единичных векторов касательных и нормалей проекций кривой.

Подставляя выражения для 1 , 1 и следующие за ними выражения в (15),

после приведения подобных членов, получаем

r 1F 1K

kL,

где

приняты

обозначения

d2s

d3s

2 k

ds2

2 ds

ds3

					(16)
K 3k	ds	d2s	k	ds		2
	1	1			1	,
		ds2			ds
1 ds			1

Обозначив	ds1	D,	(			)	ds2	E , запишем первую производную радиус-
				2	k

							ds
	ds

вектора кривой а (2) в следующем виде:

(с) МАИ, 1999-2011

6 Корчагин Д.С., Панчук К.Л./ Прикладная геометрия, вып 13, № 27 стр. 1-11

r 1D

(17)

kE,

С учетом принятых обозначений A, B и C запишем выражение второй

производной радиус-вектора кривой а (3) в виде:

(18)

r 1A 1B kC.

Выразив в (16), (17), (18) единичные векторы касательных 1, 2 и нормалей 1 ,

проекций a1 и a2 кривой a их направляющими косинусами, представим векторы r

,r компонентами по ортам i , j, k базовой системы координат xOyz кривой а в

следующем виде:

r i

D k

(19)

r i ( A B) j ( A B) k C ,

r i

( F K)

( F K) k

где 1

, 1

- направляющие косинусы (см. рис.2),

откуда очевидно

x D, y D, z E,

x A B, y A B, z C , x F K, y F K ,

z L.

Таким образом, получены зависимости производных r ,

r ,

r радиус-вектора

по длине дуги s (19) от данных, заданных на проекциях кривой, что позволяет на

основе известного из дифференциальной геометрии выражения для кручения кривой линии [2]

x y z

x y zx2 y2 z2

определить зависимость кручения рассматриваемой линии a от ее проекций a1 и a2

BL CK D AK FB E	.	(20)

k2

Из формул (2), (10), (11) вытекают следующие предложения:

1. Касательная к кривой проецируется в общем случае в касательную к проекции кривой, что соответствует известной теореме [3].

(с) МАИ, 1999-2011

Корчагин Д.С., Панчук К.Л./ Прикладная геометрия, вып 13, № 27 стр. 1-11 7 2. Касательные к проекциям кривой в их проекционно-соответственных точках определяют касательную к кривой в пространстве.

Из формул (3), (10),…,(14) вытекают следующие предложения:

1.Нормаль к кривой в пространстве в общем случае не проецируется в нормаль к проекции кривой.

2.Задание касательных к проекциям кривой в их проекционно-соответственных точках и задание в этих точках значений кривизны проекций кривой определяют: а)

трехгранник Френе пространственной кривой в точке, соответствующей ее точкам-

проекциям; б) значение кривизны пространственной кривой в этой точке.

Из формулы (20) и входящих в нее выражений вытекает следующее предложение:

задание касательных к проекциям кривой в их проекционно-соответственных точках и задание в этих точках значений кривизны проекций кривой и скоростей изменения кривизны определяют кручение пространственной кривой в этой точке.

2. Пример восстановления кривизны и кручения цилиндрической винтовой

линии по ее проекциям

Пусть цилиндрическая винтовая линия задана на плоскости проекций π1

окружностью a1, уравнения которой имеют вид: x1 R1cos t1;				y1 R1sin t2;
0	2 , а	на	плоскости проекций π2 косинусоидой a2	с уравнением
x	2 R2cos z2	t3	(рис. 3). Из условия выполнения проекционного соответствия
рассматриваемых линий a1 и a2 на комплексном чертеже вытекают следующие

равенства: R1=R2=R; t1=t3=t; x1=x2, которые, приводят к уравнению cos z2					cos .
Из него следует	z2	.	Для обеспечения	проекционной	взаимной
однозначности линий	a1	и a2	принимаем z2 ,	где λ - вещественный

коэффициент. Таким образом, φ является общим параметром в уравнениях кривых a1 и a2. Учитывая это обстоятельство, запишем уравнения радиус-векторов,

описывающих кривые a1 и a2: r1 Rcos i Rsin j, r2 Rcos i k .

(с) МАИ, 1999-2011

8 Корчагин Д.С., Панчук К.Л./ Прикладная геометрия, вып 13, № 27 стр. 1-11

Продифференцировав r1и r2 по параметру φ получим:

dr1

ds1

dr2

ds2

d ds

d d ds

где

R2 sin2 2 .

Рис. 3 Проекции винтовой линии

Откуда

определим

единичные

касательные векторы

Rsin i

sin i

cos j,

(R2 sin

2 2)1 2

Повторное дифференцирование дает выражения:

ds 2

d2s

1 1

2 2

где k

d2s1

0, k

Rcos

d2s2

R2 cos sin

d 2

(R2 sin2 2)3

d 2

(R2 sin2 2)1 2

Отсюда определим единичные векторы нормалей:

d2s

ds 2

cos i sin j,

d2s

Rsin k

2 1 2

sin

)

Теперь, зная единичные векторы касательных и нормалей, найдем выражения для их направляющих косинусов:

1 i sin ;

1 i cos ;

(с) МАИ, 1999-2011

Корчагин Д.С., Панчук К.Л./ Прикладная геометрия, вып 13, № 27 стр. 1-11 9

Rsin

2 i (R2 sin2 2)12 ;

2 k (R2 sin2 2)12 ;

Rsin

2 k (R2 sin2 2)12 ;

1 j cos ;

1 j sin .

Подставляя найденные выражения параметров в (10), (11), (12) и (13),

находим:

																						ds1											R							;
																													(R		2				2		1 2			;
																							ds						(R			)
																	ds			2					(R2 sin2 2)1 2
																				2																							;
																														(R	2				2		1 2						;
																	ds													(R		)
																												d		2s
																														1		0;
																																0;
																												ds2
													d2s															R2 sin cos
															2																														.
														ds	2					(R				2						2			2	sin			2					2 1 2			.
														ds						(R						)(R								sin				)
Откуда получаем выражения для коэффициентов:
																														A 0;
																	1											R						2								R
														B			1											R														R
																										2															2	2		;
																							(R			2				2 1 2									R		2	2		;
																	R						(R					)											R
C																										R2 sin cos																						Rsin
C			(R			2	sin		2			2 1 2					(R				2						2				2	sin			2						2 1 2					(R	2	sin	2	2 1 2
			(R				sin			)							(R						)(R									sin				)										(R		sin		)
					Rcos											(R		2	sin					2						2		1 2			2
																		2						2						2		1 2			2
																									)
																																					0,

		2					2			2													2				2 1 2
	(R	2		sin			2			2	3 2							(R					2				2 1 2
	(R			sin				)										(R						)
дающие	на				основании									формулы													(14)						окончательное															выражение			кривизны

(с) МАИ, 1999-2011

10 Корчагин Д.С., Панчук К.Л./ Прикладная геометрия, вып 13, № 27 стр. 1-11

k R2 2 , совпадающее с известной формулой [2] для вычисления кривизны

цилиндрической винтовой линии.

Для определения кручения винтовой линии найдем недостающие коэффициенты выражения (20), которые принимают следующий вид:

D			R				;
	(R	2	2	1 2
			)
E						;

		2	2	1 2
	(R		)
F			R					;
		2	2		3 2
	(R		)

K0;

L0,

после подстановки, которых в (20), получим выражение для кручения R2 2 ,

совпадающее с известной формулой [2] для вычисления кручения цилиндрической винтовой линии.

Выражение (2) дает единичный вектор касательной для рассматриваемой линии в виде:

	Rsin			Rcos

			i				j				k .

(R	2	2 1 2		(R	2	2 1 2		(R	2	2 1 2
(R		)		(R		)		(R		)

Выражение (3) дает единичный вектор нормали для рассматриваемой линии в

виде:

cos i sin j.

На основании формулы получаем единичный вектор бинормали в

виде:

sin

cos

k .

2 1 2

)

Таким образом, восстановленный по проекциям a1 и a2 трехгранник Френе,

(с) МАИ, 1999-2011

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.11.201830.18 Кб7Osobennosti_funktsionirovania_finansovyh_sistem....docx
#
30.05.2015155.03 Кб11otchet.docx
#
30.05.2015151.5 Кб55otvety.docx
#
26.09.2019360.67 Кб42otvety_finansy (1).docx
#
30.05.2015162.3 Кб12pamyatka_proforga_BGU_2013.doc
#
30.05.20152.03 Mб10pan1327.pdf
#
30.05.2015735.74 Кб9PAROL_Lekcii-MO_v_nal_sfere-NiN-2014 (1).doc
#
30.05.20155.68 Mб50Patch_clamp.docx
#
30.05.2015114.07 Кб15Patentovedenie_Kurs_lektsy.docx
#
27.11.2019184.55 Кб6Pechat_METODIChKA_VKR_EiU_docx_Vosstanovlen.docx
#
22.07.2019154.62 Кб14Pedagogika_33__33__33.doc