Федеральное агентство по образованию

ФГАОУ ВПО «УрФУ имени первого Президента России Б.Н. Ельцина»

Кафедра вычислительных методов и уравнений математической физики

Простейшие методы изучения решений дифференциального уравнения первого порядка

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ

по дисциплине «Специальные главы математики»

Преподаватель Ермакова Г.М.

Студент гр. 190302 Иванов А.В.

Номер зачетной книжки 09932108

Екатеринбург

2010

Содержание

1. Постановка задачи……………………………………………………………..	3
2. Аналитическое точное решение дифференциального уравнения………….	4
3. Решение дифференциального уравнения приближёнными методами……..	6
3.1. Решение дифференциального уравнения методом изоклин……………...	6
3.2. Решение дифференциального уравнения методом Эйлера……………….	8
3.3. Решение дифференциального уравнения методом последовательных приближений………………………………………………............................	8
3.4. Решение дифференциального уравнения основным методом Рунге-Кутта…………………………………………………………………..	10
4. Результаты решения дифференциального уравнения………………………	12
5. Вывод…………………………………………………………………………...	13
Приложение 1…………………………………………………………………….	14

1. Постановка задачи

Решить задачу Коши для дифференциального уравнения (ДУ) первого порядка при начальных условиях, используя следующие методы решения ДУ:

1. точный аналитический метод;

2. приближенный графический метод (метод изоклин);

3. приближенный аналитический метод (метод последовательных приближений);

4. приближенные численные методы (метод Эйлера, основной метод Рунге-Кутта).

2. Аналитическое точное решение дифференциального уравнения

ДУ – неоднородное линейное дифференциальное уравнение (НЛДУ) с постоянными коэффициентами. Решим его в соответствии с алгоритмом решения НЛДУ с постоянными коэффициентами:

; ;;

–некоторое решение нашего НЛДУ; ищем коэффициенты из соотношения

;

получаем ;;.

Итак,

.

Реализуя начальное условие , получаем значение:или.

Окончательно имеем

.

Протабулируем найденную функцию с шагом в точках, где:

.

Найденные значениязанесены в таблицу 2.

3. Решение дифференциального уравнения приближёнными

методами

3.1 Решение дифференциального уравнения методом изоклин

Построим поле направлений исходного ДУ с помощью изоклин. Уравнение семейства изоклин или.

Будем придавать следующие значения:

()

()

()

()

()

()

()

()

()

()

Для более точного построения интегральных кривых по построенному полю воспользуемся дополнительной информацией:

. Точки этой параболы «подозрительны» на extr.

Проверим

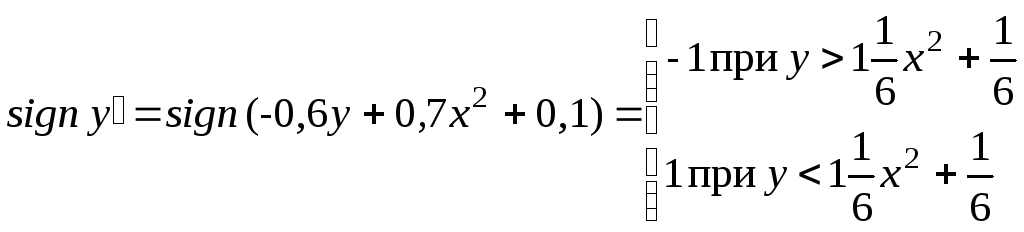
Смена знака первой производной говорит о том, что между ветвями параболы интегральные кривые убывают, а вне параболы интегральные кривые возрастают, т.е. на левой ветви параболы имеем локальный максимум, а на правой – локальный минимум. Данная «экстремальная линия» выделена на рисунке 1 зеленым цветом.

y(x) – выпуклая

y(x) – вогнутая

Смена знака второй производной говорит о том, что между ветвями параболы интегральные кривые выпуклы вниз, а вне параболы интегральные кривые выпуклы вверх.

На рисунке 1 (см. приложение 1) приведено поле направлений ДУ, интегральные кривые, а также выделена интегральная кривая, соответствующая начальному условию. Ординаты выделенной кривой в точках занесены в таблицу 2.