
отвкты на математику
.pdf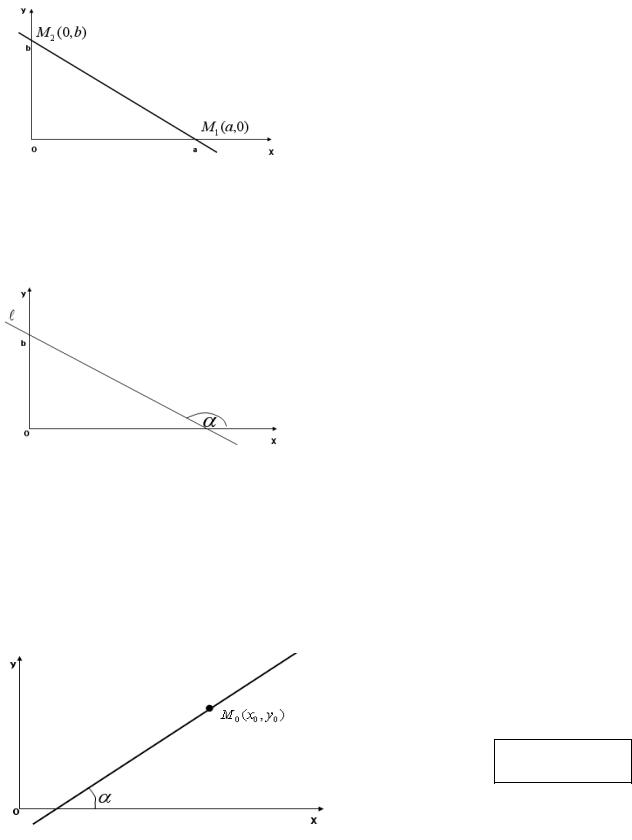
|
х х1 |
|
у у1 |
|
||||
|
х |
2 |
х |
у |
2 |
у |
|
|
|
|
|
||||||
|
|
1 |
|
|
1 |
|
||
Уравнение прямой в отрезках
Пусть прямая пересекает ось Ох в точке
М1 (а,0) , а ось Оу - в точке М 2 (0,b) .
Подставим координаты этих точек в уравнение прямой, проходящей через две точки,
у 0 |
|
x |
a |
После преобразований получим: |
|||||
b 0 |
|
a |
|||||||
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
1 |
|
|
|
|
|
|
a |
b |
||
|
|
|
|
|
|
|
|
||
Это уравнение называется уравнением прямой в отрезках, так как числа a и b указывают, какие отрезки отсекает прямая на осях координат.
19. Прямая с угловым коэффициентом.
Опр: Угловым коэффициентом прямой называется тангенс угла между прямой и
положительным |
направлением |
оси |
ОХ. |
||
Обозначается |
угловой |
коэффициент: k=tg |
|
||
(0 ) |
, где |
- |
угол между |
прямой и |
|
положительным направлением оси ОХ.
b- отрезок, который прямая отсекает на оси
ОУ
уравнение y kx b — уравнением прямой с угловым коэффициентом.
Если прямая проходит через начало координат, то b = 0 и, следовательно, уравнение этой прямой будет иметь вид у = кх.
Если прямая параллельна оси Ох, то = 0, следовательно, k= tg = 0 и уравнение примет вид у = b.
Если прямая параллельна оси Оу, то уравнение имеет вид: х = а где а — абсцисса точки пересечения прямой с осью Ох.
Прямая, проходящая через точку, в данном направлении
Пусть прямая проходит через точку M0 (x0 , y0 ) и ее направление
характеризуется конкретным угловым коэффициентом к. Уравнение этой прямой можно записать в виде:
y y0 k (
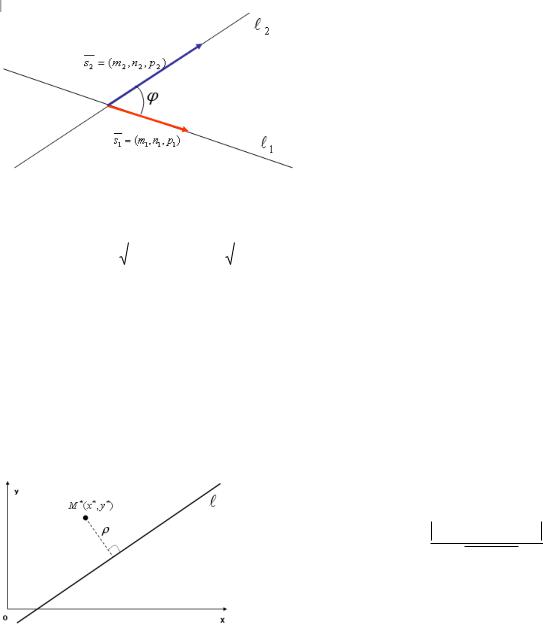
Уравнение y y0 k (x x0 ) с различными значениями к называют также уравнениями пучка прямых с центром в точке M0 (x0 , y0 ) .В этом пучке нельзя определить лишь прямую, параллельную ори Оу.
20. Угол между прямыми и расстояние от точки до прямой.
Угол между прямыми в пространстве
Пусть две прямые 1 |
и 2 заданы каноническими уравнениями: |
|
|
|
|
|
|
|
|||||||||||||
|
|
: |
x x1 |
|
y y1 |
|
|
z z1 |
и |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
m1 |
|
n1 |
|
|
p1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
: |
x x2 |
|
y y2 |
|
z z2 |
. |
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
n2 |
|
|
|
p2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Выпишем направляющие векторы этих |
||||||||||||
|
|
|
|
|
|
|
|
|
прямых: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
s1 (m1 , n1 , p1 ) , |
|
s2 (m2 , n2 , p2 ) . |
|||||||||
|
|
|
|
|
|
|
|
|
Угол между прямыми равен углу между их |
||||||||||||
|
|
|
|
|
|
|
|
|
направляющими |
|
векторами: |
||||||||||
cos |
|
|
s1 |
|
|
s2 |
|
|
|
|
m1 m2 n1 |
n2 |
p1 p2 |
|
|
. |
Для |
нахождения |
острого угла |
|
между |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
s |
s |
2 |
|
|
|
m2 |
n2 p 2 |
m2 |
n2 p |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 |
|
|
|
|
|
|
|
1 |
1 |
|
1 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
прямыми, числитель правой части следует взять по модулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ││ 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
Условие |
|
параллельности |
|
|
прямых: |
s1 ││ s2 , |
или |
в |
|||||||||||||||||||||||
координатной форме: |
m1 |
|
|
n1 |
|
|
p1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
n2 |
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Условие |
перпендикулярности |
прямых: 1 |
|
2 |
s1 s2 , а |
в |
||||||||||||||||||||||||
координатной форме: m1 m2 n1 n2 p1 p2 |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Расстояние от точки до прямой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть заданы координаты точки М * (х* , у* ) |
и |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнение прямой : Ах+Ву+С=0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Расстояние от точки до прямой есть длина перпендикуляра, опущенного из точки на прямую:
Ах* Ву * С
(М * , )

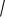 А2 В2
А2 В2
21. Эллипс.

Каноническое уравнение эллипса, с центром в начале координат:
Полуосями этого эллипса являются по оси ОХотрезок а, и по оси ОУотрезок b. Таким образом, эллипс имеет две оси симметрии: ось ОХ и ось ОУ. Четыре вершины: точки с
координатами (-а;0); (а;0); (0;-b); (0;b). |
Если величина а |
b, то |
. На |
большей оси в точках с координатами |
и |
(с, 0) находятся фокусы эллипса. |
|
Эксцентриситетом эллипса называется |
,т.е. отношение половины расстояния между |
||
фокусами к большей полуоси. Для эллипса
Характеристическое свойство эллипса: Эллипсом называется геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, постоянна и равна удвоенной большей полуоси.
22.
-каноническое уравнение эллипса,
центр симметрии которого находится в точке
Q( ,
,
полуоси эллипса: по ОХ равна a, по оси ОУ
равна b. |
|
|
|
Фокусы |
находятся |
в |
точках: |
Пример: Построить эллипс, уравнение которого:
,найти его фокусы
и эксцентриситет.
Решение: Центром симметрии эллипса является точка Q(2; -3), полуоси эллипса: а=3; b=2; ; фокусы эллипса находятся в точках:
.
23. Гипербола.
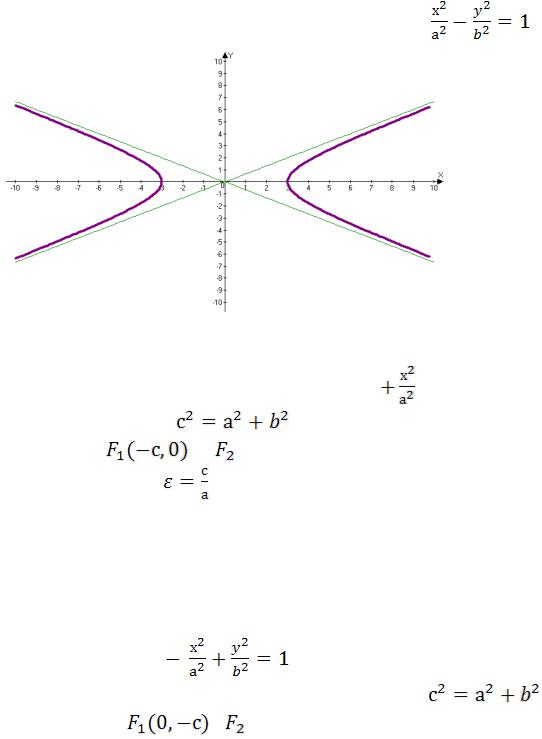
Каноническое уравнение гиперболы, с центром в начале координат:
Полуосями этой гиперболы являются по оси ОХотрезок а, и по оси ОУотрезок b. Таким образом, гипербола имеет две оси симметрии: ось ОХ и ось ОУ. Четыре вершины: точки с
координатами (-а;0); (а;0); |
(0;-b); |
(0;b). |
Если величина |
, то полуось а называется |
|
действительной, b-мнимой. |
|
|
|
. На продолжении действительной оси в точках с |
|
координатами |
и |
(с, |
0) |
находятся фокусы |
гиперболы. Эксцентриситетом |
гиперболы называется |
,т.е. |
отношение половины |
расстояния между фокусами к |
||
действительной полуоси. Для гиперболы 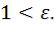 Гипербола имеет две асимптоты, уравнения которых:
Гипербола имеет две асимптоты, уравнения которых:
24. 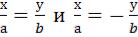
Гиперболой, сопряженной к данной, называется гипербола:
Для этой гиперболы а- мнимая полуось, b-действительная. |
. Фокусы |
|
находятся в точках: |
и (0, с). |
|
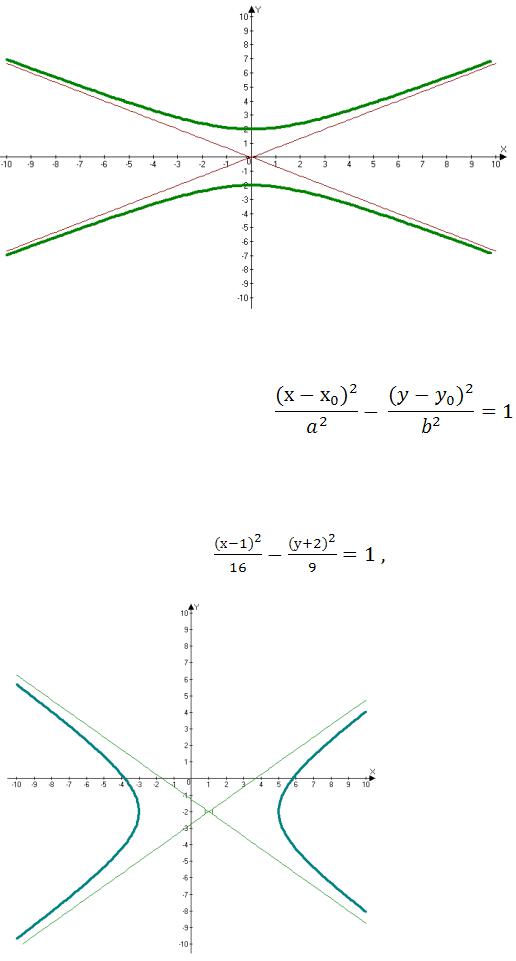
Характеристическое свойство гиперболы:
гиперболой называется геометрическое место точек, модуль разности расстояний от каждой из которых до двух данных точек этой же плоскости, называемых фокусами постоянна и равна
удвоенной действительной полуоси. |
-каноническое |
уравнение гиперболы, центр симметрии которого находится в точке Q(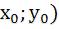 ,полуоси гиперболы: действительная по ОХ равна a, мнимая по оси ОУ равна b.
,полуоси гиперболы: действительная по ОХ равна a, мнимая по оси ОУ равна b.
Фокусы находятся в точках: 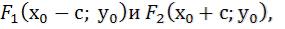 Пример: Построить гиперболу, каноническое уравнение которой:
Пример: Построить гиперболу, каноническое уравнение которой:
найти фокусы и эксцентриситет.
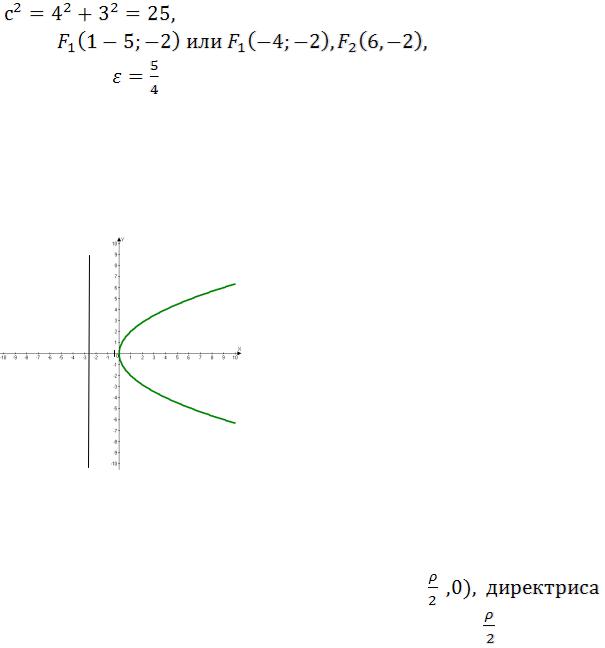
Решение: центр симметрии гиперболы находится в точке:Q(1,-2), действительная полуось а=4; мнимая полуось b=3.
с=5.
Фокусы:
Эксцентриситет: =1,25.
25. Парабола.
26. Парабола
Каноническое уравнение параболы с вершиной в начале координат: 
Характеристическое свойство параболы:
параболой называется геометрическое место точек, равноудаленных от точки, называемой фокусом и от прямой, называемой директрисой.
Расстояние от фокуса до директрисы называется параметром параболы и обозначается  . Вершина параболы находится посередине между фокусом и директрисой. Фокус находится на оси симметрии внутри параболы, для данной параболы F(
. Вершина параболы находится посередине между фокусом и директрисой. Фокус находится на оси симметрии внутри параболы, для данной параболы F(
перпендикулярна оси симметрии, находится вне параболы, ее уравнение х = .
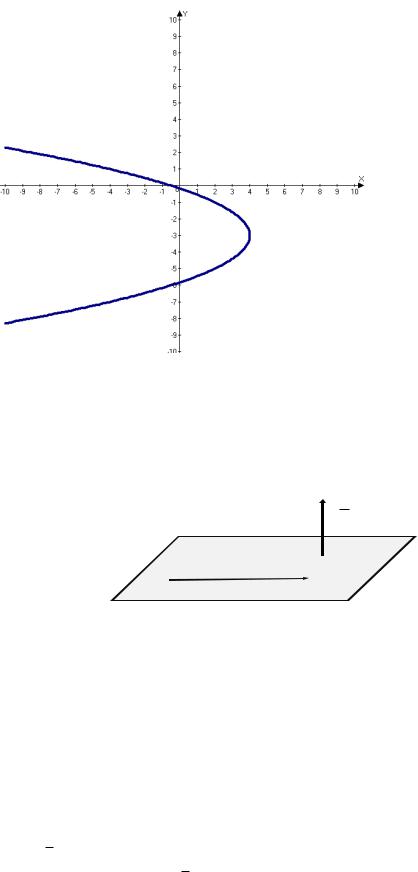
Пример: Построить параболу, определить ее фокус и директрису:
27. -4·(x-4)=(y+3)²
Решение: Уравнение параболы в общем виде:
28.2·p·(x-a)=(y-b)²
Внашем уравнении: a=4,b=-3, 2p=4, p=2.
Фокус:F(a-p/2;b)=F(3;-3) Директриса x=p/2+a x=5.
Вершина параболы находится в точке Q(4; -3),
29. Плоскость по точке и нормали.
Опр.: Нормалью к плоскости называется вектор, перпендикулярный к данной плоскости.
n( A, B, C)
M 0 ( x0 , y0 , z0 )
М(x,y,z)
Пусть |
необходимо |
составить уравнение плоскости, |
проходящей |
|
через заданную |
точку |
|||||
|
|
|
|
|
|
|
|
|
|||
M 0 (x0 , y0 , z0 ) и перпендикулярной вектору n ( A, B,C) . |
|
|
|
|
|||||||
Предположим, |
что такая плоскость построена, |
возьмем на |
ней произвольную |
точку |
|||||||
|
|
|
|
|
|
|
|
||||
М(x,y,z) |
. Составим |
вектор М 0 М (х х0 , y y0 , z z0 ) . Вектор |
|
М 0 М перпендикулярен |
|||||||
|
|
|
|
|
|
|
|
|
вектору n , следовательно, их скалярное произведение |
равно нулю: n M 0 M 0 , это условие |
|||||||
имеет вид:: |
|
|
|
|
|
|||
|
|
|
A(x x0 ) B( y y0 ) C(z z0 ) 0 |
|
||||
|
|
|
|
|||||
Данный способ задания плоскости называется |
плоскость по точке М 0 ( х0 , y0 , z0 ) и |
|||||||
нормали n ( A, B,C) . Имея уравнение плоскости в общем виде: Ax+ By+ Cz+ D=0, можно выписать нормаль к плоскости n ( A, B,C) .
Пример: Составить уравнение плоскости, проходящей через точку А(1,2,-3), параллельно плоскости 3x-4y+5z-2=0
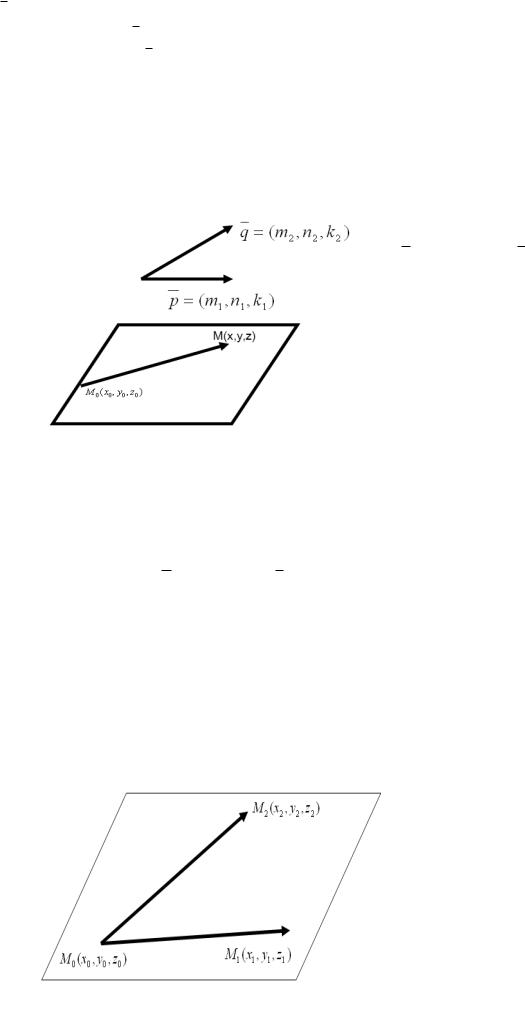
Решение: Выпишем нормаль к плоскости, т.е. вектор перпендикулярный плоскости: n (3, 4,5) . Так как необходимо построить плоскость параллельную данной, то можно
использовать вектор n в качестве нормали к искомой плоскости. Составляем уравнение плоскости по точке А и нормали n : 3 (x 1) 4 ( y 2) 5 (z 3) 0 после преобразования получим:
3x-4y+5z+20=0
Ответ: 3x-4y+5z+20=0.
30. Плоскость по точке и двум направляющим.
Опр.: Два неколлинеарных вектора, параллельные плоскости, называются направляющими векторами этой плоскости.
Пусть необходимо составить уравнение плоскости, проходящей через заданную точку
M 0 (x0 , y0 , z0 )
заданным
p (m1 , n1 , k1 )
и параллельную векторам и q (m2 , n2 , k2 ) .
Считаем, |
что такая плоскость |
построена, возьмем произвольную |
|
точку М(x,y,z) этой плоскости и |
|
составим |
вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М 0 М (х х0 , y y0 , z z0 ) . |
||||||
При |
|
|
|
любом расположении точки М, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
векторы М 0 М , p, q компланарны, |
|||||||
т.е. |
|
|
|
их смешанное произведение равно |
|||||||||||||||
0. |
|
|
|
|
|
|
|
|
|
|
|
Запишем это условие в векторной |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
форме: М 0 М p q 0 . Запишем в координатной форме: |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х х0 |
y y0 |
z z0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
n1 |
k1 |
|
||||||||
|
|
|
|
|
|
|
|
m2 |
n2 |
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Данный способ задания плоскости называется плоскость по точке M 0 (x0 , y0 , z0 ) и двум направляющим векторам p (m1 , n1 , k1 ) и q (m2 , n2 , k2 ) .
|
31. Плоскость по трем точкам и уравнение в отрезках. |
|
Уравнение плоскости, проходящей через три заданные точки |
|
Пусть необходимо составить уравнение плоскости, проходящей через три заданные , не |
|
лежащие на одной прямой, точки: М 0 (x0 , y0 , z0 ), M1 (x1 , y1 , z1 ), M 2 (x2 , y2 , z2 ) |
|
Считаем, что такая |
|
плоскость построена, составим |
два |
вектора |

М 0 М1 (x1 x0 , y1 y0 , z1 z0 ) и M 0 M 2 (x2 x0 , y2 y0 , z2 z0 ) .
Эти векторы являются направляющими векторами плоскости. Составим уравнение
плоскости по точке М 0 и двум направляющим векторам М 0 М1иМ 0 М 2 .
|
|
x x0 |
y y0 |
z z0 |
|
|
|
||||
|
|
x1 x0 |
y1 y0 |
z1 z0 |
0 |
|
|
x2 x0 |
y2 y0 |
z2 z0 |
|
|
|
|
|
|
|
Данный способ задания плоскости называется плоскость по трем точкам. Пример: Составить уравнение плоскости АВС, если даны координаты точек:
A 3; 2;2 ; B 1; 3;1 ; C 2;0;4
Решение: Составим уравнение плоскости ABC по трем точкам:
|
x 3 |
y 2 |
z 2 |
|
x 3 |
y 2 |
z 2 |
|
|
|
|
|
|||||||
|
1 3 |
3 2 |
1 2 |
0 , |
2 |
1 |
1 |
|
0 , |
|
2 3 |
0 2 |
4 2 |
|
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Найдем разложение определителя по первой строке:
x 3 2 2 y 2 4 1 z 2 4 1 0 ,
5 y 2 5 z 2 0 ,
5y 5z 20 0 , разделим уравнение на 5: y z 4 0 .
Ответ: y z 4 0 .
Уравнение плоскости в отрезках
Пусть необходимо составить уравнение плоскости, отсекающей на осях координат OX, OY, OZ соответственно отрезки a,b,c, т.е. плоскость проходит через точки A(a,0,0), B(0,b,0) и
C(0,0,c). |
|
|
|
|
|
|
|
||
|
|
Подставим координаты этих точек в |
|||||||
уравнение |
плоскости |
по трем |
точкам: |
||||||
|
x a |
y |
z |
|
|
|
x a y |
z |
|
|
|
|
|
||||||
|
0 a |
b |
0 0 |
0 , |
|
|
a b |
0 |
0 , |
|
0 a |
0 0 |
c 0 |
|
|
|
a 0 |
c |
|
|
|
|
|
|
|
|
|
|
|
преобразуем определитель, получим:
b c x a c y a b z a b c 0 или
b c x a c y a b z a b c
разделим уравнение на abc, получим:
ax by cz 1
32. Угол между плоскостями и расстояние от точки до плоскости.
Угол между плоскостями Пусть заданы две плоскости 1 : А1 х В1 у С1 z D1 0
2 : А2 х В2 у C2 z D2 0 .

|
|
Углом между |
плоскостями называется |
|||
один из двухгранных углов, образованных при |
||||||
пересечении этих плоскостей. Выпишем нормали |
||||||
|
|
|
|
|
|
|
к |
плоскостям: |
|
n1 ( A1 , B1 ,C1 ) |
и |
||
|
|
|
||||
|
n2 ( A2 , B2 ,C2 ) . Угол между плоскостями равен |
|||||
углу между нормалями к плоскостям, т.е. Косинус |
||||||
угла между плоскостями вычисляется по формуле: |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
cos |
|
n1 |
|
n2 |
|
|
|
A1 A2 B1 |
|
B2 C1 |
C2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
n |
n |
2 |
|
|
|
A2 |
B2 C 2 |
|
|
A2 B2 |
C 2 |
|
|
||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
2 |
|
|
|
2 |
2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
Условие перпендикулярности плоскостей: |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
n1 |
n2 , |
это условие в векторной |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
форме: |
|
n1 n2 |
0 , |
или |
в координатной форме: |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 A2 B1 B2 C1 C2 0 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Условие параллельности плоскостей: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
n1 |
n2 |
, или в координатной форме: |
|||||||||||||||||||
координаты векторов должны быть пропорциональны: |
|
A1 |
|
|
|
B1 |
|
C1 |
|
|
|
||||||||||||||||||||||||||||
|
A2 |
|
|
B2 |
C2 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Расстояние от точки до плоскости |
|
|
|
Пусть задана |
точка: M * (x* , y* , z* ) |
и |
плоскость: |
Ax By Cz D 0 |
расстояние d от точки |
до |
плоскости |
находится по формуле: |
|
|
|
|
d |
|
Ax* By * Cz* D |
|
|
|||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A2 B 2 |
C 2 |
|
|||||
|
|
|
|
|
||||
33. Прямая в пространстве по точке и направляющему вектору. |
|
|
|
|
|
|
||
Пусть необходимо составить уравнение прямой , проходящей через точку |
М 0 (х0 , у0 , z0 ) , |
|||||||
параллельно заданному вектору s (m, n, p) .Возьмем произвольную точку М(x,y,z) на прямой
.
Вектор М 0 М (x x0 , y y0 , z z0 ) параллелен вектору s , следовательно , их координаты пропорциональны:
|
х х0 |
|
y y0 |
|
z z0 |
|
|
m |
n |
p |
|
||
|
|
|
|
|||
|
|
|
|
|
|
|
Данный способ задания прямой называется прямая по точке М 0 (х0 , у0 , z0 ) и направляющему вектору s (m, n, p) . Уравнение прямой получено в каноническом виде.
34. Прямая в пространстве по двум точкам. |
|
|
Пусть необходимо составить уравнение прямой |
, проходящей через две заданные точки: |
|
|
|
|
М 0 (х0 , у0 , z0 ) и M1 (x1 , y1 , z1 ) . Вектор |
M 0 M1 (x1 x0 , y1 y0 , z1 z0 ) является |
|
