
may05119
.pdf
11
О бращ аем внимание, ч т о в ч ис л ит е л е у вс ех эл емент ов пос л е доват ел ь - нос т и с т оит 1, ав знаменат е л е квадрат не ч ет ныхч ис ел . Н еч ет ные ч ис л а
запис ываю т с я с помощ ь ю формул ы 2n −1, где n = |
... , ,в3,ит2,1 оге пол у- |
||
ч аем, ч т о общ ийч л е н пос л едоват е л ь нос т и имеет вид: |
xn = |
1 |
. |
(2n - 1)2 |
|||
b)12;14 ; 2 79 ; 3161 ; 3 256 ;...
П ере пиш е м эл емент ы пос л едоват ел ь нос т и в виде не правил ь ныхдробей:
1; 9 ; |
25 |
; 49 ; |
81 |
;... . О ч е видно, ч т о в |
ч ис л ит е л е и знаме нат ел е |
дробей |
|||||||||||||
4 |
9 |
16 |
25 |
|
|
32 |
|
52 |
|
72 |
|
92 |
|
|
|
|
|
||
предс т авл е ны квадрат ы ч ис ел , т .е. 1; |
; |
; |
; |
;... |
. В ч ис л ит е л е с т о- |
||||||||||||||
22 |
|
|
52 |
||||||||||||||||
|
|
|
|
|
|
|
32 |
42 |
|
|
|
|
|
|
|||||
ят квадрат ы неч е т ныхч ис е л : (2n - 1)2 , в знаменат е л е – n2 , где |
n = |
... . , 3, 2,1 |
|||||||||||||||||
В резул ь т ат е |
общ ий ч л ен пос л едоват е л ь нос т и |
име ет |
вид: |
xn = |
(2n - 1)2 |
|
|||||||||||||
n2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
æ 2n - 1ö2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ил и |
xn |
= ç |
|
|
|
÷ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|||
3.П ол ь зуяс ь рекурре нт ной формул ой, найт и общ ий ч л ен пос л едоват е л ь - нос т и:
a) x1 =1, xn+1 = xn + 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уч ит ывая |
ис ходны е |
данны е, |
выпиш ем |
не с кол ь ко ч л енов |
пос л едова- |
|
|
||||||||||
т ел ь нос т и: |
|
|
+ |
2 |
xx1 |
3x= 41=+1 |
|
= |
|
|
|
|
|
|
|||
|
|
|
+ |
|
x x2 |
3x3= 72+=1 |
|
= |
|
|
|
|
|
|
|||
|
|
|
+ |
4 |
xx |
3 |
3x =10=+ |
|
= |
|
|
|
|
|
|
||
|
|
|
|
|
|
3 1 |
|
|
|
|
|
|
|
|
|||
|
|
|
+ |
|
x x= |
3x==13+ |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
4 |
|
5 |
4 1 |
|
|
|
|
|
|
|
|
|
П ол уч ае м |
пос л е доват ел ь нос т ь : |
|
|
|
|
;... |
|
. 13П е;репиш10 ; 7;ем14; пол уч ен- |
|
|
|||||||
ную пос л едоват е л ь нос т ь : |
- |
- |
|
- |
|
|
- |
|
- |
;... |
,2ил и15 ; 2 |
12 ; 2 |
9; 2 |
36; 2 |
|||
|
|
× |
- |
× |
- |
|
× |
- |
× |
- |
× |
- ;... |
2 5 |
3; 2 4 |
3; 2 |
3 3; 2 2 |
|
Т огдаобщ ийч л е н пос л е доват е л ь нос т и: |
xn |
= 3n - 2 . |
|
|
|
|
|
|
|||||||||
b) x1 = 2 , xn+1 = 3xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уч ит ывая |
ис ходны е |
данны е, |
выпиш ем |
не с кол ь ко ч л енов |
пос л едова- |
|
|
||||||||||
т ел ь нос т и: |
|
|
|
|
x |
|
|
x |
× 33 =2 |
=6= |
|
= |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
2 |
1 1 |
× 32 =2 × 9 3=2 =18= = |
|
|
|
||||||
|
|
+ |
|
xx2 |
|
x3 |
|
2 1 |
|
|
|
||||||
|
|
+ |
|
x3 |
x4 |
3 1 |
|
× 33 =2 ×27=32 ==54 = |
|
|
|
||||||
|
|
+ |
|
x4 |
x5 |
4 |
1 |
|
× 34 =2 |
× 81= 23 |
== 162= |
|
|
|
|||
В ит оге пол уч аем пос л е доват е л ь нос т ь :
× 4 0;...× ,31 3 ×2;× 2 3 ×2; 3 2; 3 2;2 3
т огдаобщ ийч л ен имее т вид: xn = x1 × 3n−1 .
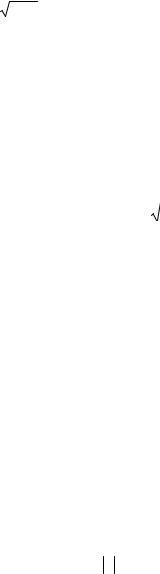
12
Г л а в а 2. Пр едел функ ции. Н епр ер ы в ностьфунк ции.
§1. Общ ее понятие функ ции.
Опр едел ение. П ус т ь даны двач ис л овых множ е с т ваX и Y. Е с л и каж дому
эл емент у X, |
по опре дел е нному правил у, с т авит с я в с оот вет с т вие одно |
|
опре де л енное знач е ние пере менной y Y, т о говорят , ч т о y ес т ь однознач - |
||
ная функция от |
, и обознач аю т y = f (x) . |
|
П ереме нная |
называет с я неза вис им о й перем енно й, ил и а ргум енто м . |
|
Совокупнос т ь |
вс ех знач ений аргумент а , дл я кот оры х функция |
|
y = f (x) определ е на, |
называет с я о б ла с тью о пределения функции и обозна- |
|
ч ае т с я ч ере з D( f ) . |
|
|
Совокупнос т ь вс ех знач ений, принимаемых переме нной y , называ- |
|
ет с я обл ас т ь ю знач е нийфункции y = f (x) и обознач ае т с я - E( f ). |
|
Н апример, y = x -1 : D(y)=[1, +∞), E(y)=[0, +∞) |
|
Знач ения функции |
f (x) при x = a обознач аю т f (a). |
Графиком функции |
y = f (x) называет с я множ ес т во т оч ек пл ос кос т и |
xOy с координат ами [x , f (x)], x X .
Ф ункция, вс е знач ения кот орой равны меж ду с обой, называет с я по -
с то янно й и обознач ае т с я с . |
|
|
|
|
|
|
|
Способы за да ния функ ций |
|
||||
1. |
А на л итическ ий – завис имос т ь |
меж ду пере ме нными опреде л яе т с я с |
||||
помощ ь ю формул ы , например, |
|
= |
|
=. |
|
|
2 , |
1 - x2 |
y x |
||||
2. |
Т а бл ичны й , например, т абл ицы |
т ригономет рич ес ких функций, л ога- |
||||
рифмов, рас пис ание движ е ния пое здов, кот орое определ яет ме с т опол ож е - ние поездав от де л ь ные момент ы време ни.
3. Г р а фическ ий – ис пол ь зует с я в практ ике физич е с ких изме рений, когда с оот вет с т вие ме ж ду переменными x и y задае т с я пос редс т вом графика.
К л а ссифик а ция функ ций .
П рос т ейш ие эл еме нт арные функции: пос т оянная функция f (x) = c ; с т е пен-
ная функция |
f (x) = xa , "a ; показат е л ь ная функция f (x) = ax , a > 0, a ¹ 1; л ога- |
|
рифмич ес кая функция |
f (x) = loga x, a > 0, a ¹ 1; т ригономе т рич ес кие функции |
|
( ) = sin x , |
f( )x= cos x , |
(f )x= tgx , f (x) = ctgx ; обратf x ные т ригономет рич ес кие |
функции f (x) = arcsin x , |
f (x) = arc cos x , f (x) = arctgx , f (x) = arcctgx . |
|
Вс е функции, пол уч аемые с помощ ь ю коне ч ного ч ис л аарифмет ич е - с ких дейс т вий над прос т ейш ими эл емент арными функциями, ат акж е с у- перпозицией (ил и нал ож ение м) эт их функций, с ос т авл яю т кл ас с эл емен- т арныхфункций, например: f (x) = x , f (x) = lg3 arctg2x + sin 3x .
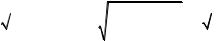
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
И ме ет ме с т о с л едую щ ая к л а ссифик а ция эл ем ента р ны хфунк ций : |
|||||||||||||
1. |
Ц ел ая рационал ь ная функция ил и ал ге браич ес кий многоч л е н с т е пени |
|||||||||||||
m: |
P(x) = a xm + a xm−1 + ...+ a |
x + a , |
m ³ 0, |
m Î Z, |
a , a ,..., a |
m |
– л ю бы е ч ис л а, |
|||||||
|
0 |
1 |
m−1 |
m |
|
|
0 |
1 |
|
|
|
|
|
|
коэффициент ы, |
a0 ¹ 0. |
М ногоч л ен |
первой с т епе ни |
|
называет с я л ине йной |
|||||||||
функцией. |
|
|
|
|
a xm + a xm−1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
+ ...+ a |
|
|
x + a |
|||||
2. |
Д робно-рационал ь ная функция: |
R(x) = |
0 |
1 |
|
|
m−1 |
m |
. |
|||||
b xn + b xn−1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
+ ...+ b |
|
x + b |
||||||
|
|
|
|
|
|
0 |
1 |
|
|
n−1 |
|
n |
||
3. |
И ррационал ь ная функция – функция, пол уч е нная с помощ ь ю конеч ного |
|||||||||||||
ч ис л ас уперпозиций и ч е т ырех арифмет ич е с кихде йс т вий над с т епе нными функциями какс цел ыми, т аки с дробными показат ел ями и не явл яю щ аяс я
|
|
|
|
|
|
|
|
2 |
+ (5 |
|
+ x)3 . |
|
рационал ь ной, например, f (x) = |
|
+ x , f (x) = |
5x |
+ 4x - 7 |
|
|||||||
x |
x |
|||||||||||
3x |
2 |
|||||||||||
|
|
|
|
|
|
|
-8x + 4 |
|||||
4. Т ранс ценде нт ная функция – не |
явл яю щ аяс я рационал ь ной ил и ирра- |
|||||||||||
ционал ь ной, например, f (x) = sin x , |
f (x) = sin x + x |
и т .д. |
||||||||||
Ф |
ункция |
f (x) |
называет с я четно й, ес л и |
f (-x) = f (x), "x . |
||||||||
Ф |
ункция |
f (x) |
называет с я нечетно й, ес л и |
f (-x) = - f (x), "x . |
||||||||
График ч ет ной функции с иммет рич ен от нос ит ел ь но ос и ординат , а неч ет нойот нос ит е л ь но нач ал акоординат .
Ф |
ункция называет с я перио дичес ко й в обл ас т и опре дел ения, ес л и с у- |
|||||||||
щ е с т вует т акое ч ис л о T ¹ 0, ч т о: |
|
|
|
|
||||||
1. |
дл я л ю бых |
|
( ),Î |
Î |
+(x) .D |
T |
x xx D |
|
||
2. |
( |
+ ) = |
(x)f, ч исTлfоxT называет с я периодом функции f . |
|||||||
П римерами периодич ес ких функций, |
явл яю т с я т ригономет рич ес кие |
|||||||||
функции y = sin x |
и |
y = cos x с |
периодом |
T = 2π , т .е . при изме нении аргу- |
||||||
мент анач ис л о, крат ное 2π , знач е ние функции ос т ает с я пре ж ним. |
||||||||||
Ф |
ункция f (x) |
называе т с я во зра с та ю щ ей (уб ы ва ю щей) в обл ас т и оп- |
||||||||
редел е ния, |
ес л и дл я л ю бых x1 |
и x2 |
из обл ас т и опре дел ения функции т аких, |
|||||||
ч т о x1 < x2 выпол няет с я |
( 1) < |
(x2 f) ( f (x1 ) > |
(x2 f)).Фf ункцияx |
f (x) называет с я |
||||||
нево зра с та ю щей (неуб ы ва ю щей) в обл ас т и определ е ния, |
е с л и дл я л ю бых |
|||||||||
x1 и x2 |
из обл ас т и определ ения функции т аких, ч т о x1 £ x2 выпол няет с я |
|||||||||
( 1 ) £ |
(x2 f) |
( f (x1 ) ³ |
(x2 f)). Всf xе эт и функции называю т с я монот онными. |
|||||||
Ф |
ункция называе т с я о гра ниченно й с верху(с низу) на множ ес т ве X, |
|||||||||
ес л и с ущ е с т вует ч ис л о M (m) т акое, ч т о дл я л ю бого x Î X |
выпол няе т с я не - |
|||||||||
равенс т во |
( )£ |
|
( ( |
)³ m). x f |
Mf x |
|
|
|
||
Ф ункция, огранич е нная и с верху и с низу, называе т с я о гра ниченно й наэт ом множ е с т ве .
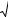
|
|
|
14 |
|
|
Е с л и |
на некот ором |
проме ж ут ке Х |
опреде л ена функция z = ϕ(x) с |
||
множ ес т вом знач е ний Z , |
анамнож е с т ве |
Z опре де л енафункция |
= y(z),f |
||
т о функция |
= [ϕ(xy)] называетf |
с я с ло ж но й функцией от х , апере ме нная z |
|||
- проме ж ут оч нойпереме ннойс л ож нойфункции. |
|
||||
П ус т ь |
X и Y - не кот оры е множ е с т ваи пус т ь заданафункция |
f , т .е. |
|||
множ ес т во пар ч ис е л (x, y), |
, Y ,xyв котX ором каж дое ч ис л о х входит в |
||||
одну и т ол ько одну пару, акаж дое ч ис л о y , - по крайнеймере , в одну пару.
Е с л и в каж дой паре эт ого множ ес т вач ис л а х |
и y поменят ь ме с т ами, т о |
||||||
пол уч им множ е с т во пар ч ис е л |
(y, x), кот орое |
называет с я о б ра тно й функ- |
|||||
цией ϕ к функции f . О брат ную |
функцию обознач аю т x = ϕ(y). Н апример, |
||||||
y = x2 и x = ± |
|
; y = ln x и x = ey . |
|
|
|||
y |
|
|
|||||
§2. Пр едел |
функ ции в точк е |
|
|||||
П ус т ь функция |
f (x) опреде л е нананекот ором множ е с т ве Х и пус т ь |
||||||
т оч каa X |
ил и a X . |
Возь ме м из Х пос л едоват ел ь нос т ь т оч ек, от л ич ных |
|||||
от а : x1, x2 , |
x3 ,..., xn |
с ходящ ую с я к а . Знач е ние функции в т оч кахэт ой по- |
|||||
с л едоват ел ь нос т и т акж е образую т ч ис л овую пос л е доват е л ь нос т ь f (x1 ), f (x2 ), f (x3 ),..., f (xn )
Опр едел ение 1. Ч ис л о b называет с я предел ом функции |
y = f (x) , |
в т оч ке а , |
|
||||||||||||||||||||||
ес л и дл я л ю бой пос л едоват е л ь нос т и знач ений аргумент а x1, x2 , x3 ,..., xn с хо- |
|
||||||||||||||||||||||||
дящ ейс я к а |
и с ос т оящ |
ейиз ч ис ел xn |
¹ a , с оот вет с т вую щ ая пос л е доват ел ь - |
|
|||||||||||||||||||||
нос т ь знач е нийфункции |
f (x1 ), f (x2 ), |
f (x3 ),..., f (xn ) |
с ходит с я кч ис л у b. |
|
|||||||||||||||||||||
Опр едел ение 2. Ч ис л о b называет с я предело м функции |
= y(x)f, |
в т оч ке а , |
|
||||||||||||||||||||||
ес л и дл я л ю бого пол ож ит ел ь ного ч ис л аε |
|
|
с ущ е с т вует т акое ч ис л о d, зави- |
|
|||||||||||||||||||||
с ящ ее от e, |
δ > 0 , ч т о дл я вс ех x ¹ a , |
удовл ет воряю щ их ус л овию |
|
x - a |
|
< δ , |
|
||||||||||||||||||
|
|
|
|||||||||||||||||||||||
выпол няет с я нераве нс т во |
|
f (x) - b |
|
< ε ил и |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
( |
)( |
( ) |
)( |
|
|
|
, |
|
0 |
, |
|
|
) |
|
|
0( ) b |
|
< εx -f |
|
Þa <xδ -a xx ¹X |
Î " |
||||
|
|
|
|
|
|
|
|
||||||||||||||||||
О бознач аю т эт о т ак lim ( ) = b fилxи |
f (x) ® b |
при x → a |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
x→a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В опре дел ениях не |
т ребует с я, |
ч т обы |
функция был а опреде л ена в |
|
|||||||||||||||||||||
пре дел ь ной т оч ке , |
но функция дол ж на быт ь определ ена к какой-нибудь |
|
|||||||||||||||||||||||
окрес т нос т и предел ь нойт оч ки, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Опр едел ение 3. Ес л и x → a и x < a , т о x ® a− |
(x ® a - 0) . Соот вет с т вую щ ий |
|
|||||||||||||||||||||||
пре дел называе т с я л ево с то ро нним предело м . |
lim |
( ) = b f |
x |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→a− |
|
|
|
|
|
|
|
|
|
||
Опр едел ение 4. Ес л и x → a и x > a , т о x ® a+ |
(x ® a + 0) . Соот вет с т вую щ ий |
|
|||||||||||||||||||||||
пре дел называе т с я пра во с то ро нним предело м . lim |
( ) = b .f x |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→a+ |
|
|
|
|
|
|
|
|
|
||

15
П редпол агает с я, ч т о функция опре дел енананекот ором проме ж ут ке с л е ва (ил и с права) от преде л ь нойт оч ки.
Т еор ем а . Ф ункция y = f (x) |
имее т в т оч ке а предел |
т огдаи т ол ь ко т огда, |
|
когдав эт ой т оч ке с ущ ес т вует как л евос т оронний, |
т ак и правос т оронний |
||
пре дел ы и они равны . |
|
|
|
Опр едел ение |
5. Ч ис л о b |
называет с я предело м |
функции y = f (x) при |
x → ∞ , ес л и |
дл я л ю бого пол ож ит е л ь ного e, найде т с я пол ож ит ел ь ное ч ис - |
||
л о δ т акое , ч т о дл я вс ехзнач е нийаргумент а x , удовл е т воряю щ ихус л овию x > d , выпол няет с я f (x) - b < e .
Символ ич ес кая запис ь опреде л ения:
("e > 0) ($d = d (e ) > 0)("x Î X : x < d ): f (x) - b < e .
Основ ны е св ой ств а пр едел ов .
1. |
П ус т ь |
функции |
f (x) и |
g(x) |
заданы наодном и т ом ж е множ ес т ве Х и |
|||||||||||
имею т в т оч ке а |
конеч ные пре дел ы, равные с оот ве т с т ве нно b и c, т о функ- |
|||||||||||||||
ции f (x) ± g (x) , |
|
f (x)× g (x), |
f (x)/ g (x) |
т акж е имею т |
в т оч ке |
а конеч ные |
||||||||||
пре дел ы, равные с оот вет с т венно b± c, b× c, b/c (с ¹0) . |
|
|
|
|||||||||||||
2. |
П ус т ь |
функции |
f (x) , g(x) |
и |
h(x) |
опре дел ены |
в некот орой окрес т нос т и |
|||||||||
т оч ки а , |
заис кл ю ч е ние м, |
быт ь |
мож ет , |
с амой т оч ки а , и функции |
f (x) и |
|||||||||||
h (x) имею т в эт ойт оч ке а |
предел , равныйb, т .е. |
→ |
= |
) =( b . Пlimxусhт ь), (f x lim |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
→a x |
x |
a |
|
кроме т ого, |
выпол няю т с я |
нераве нс т ва |
( ) £ |
£ |
x)h.( Т (огдаx) g f функцияx |
|||||||||||
g (x) т акж е име ет |
предел x→a |
) =( b .glimx |
|
|
|
|
|
|||||||||
3. |
П редел пос т ояннойраве н с амойпос т оянной, т .е. lim c = c , где c = const . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x→a |
|
|
|
4. |
П редел с т е пени функции равен т ой ж е с т епе ни предел аос нования, т .е. |
|||||||||||||||
|
n |
( ) |
æ |
|
|
ön |
|
|
|
|
|
|
|
|
|
|
x→x0 |
= ç lim |
(x)÷f |
flimx |
|
|
|
|
|
|
|
|
|||||
|
è x→ x0 |
|
ø |
|
|
|
|
|
|
|
|
|
|
|||
|
|
§3. Беск онечно м а л ы е и беск онечно бол ьш ие функ ции |
|
|
||||||||||||
Опр едел ение 1. |
Ф |
ункция |
f (x) |
называет с я б ес ко нечно м а ло й |
при |
x → а , |
||||||||||
ес л и lim f (x) = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x→a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Опр едел ение 2. Ф |
ункция |
f (x) |
называе т с я б ес ко нечно |
б о льшо й при |
x → а , |
|||||||||||
ес л и lim f (x) = ¥ . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x→a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Св ой ств а беск онечно м а л ы хи беск онечно бол ьш ихфунк ций . |
|||||||||||||||
1. |
Д л я выпол не ния равенс т ва x→a |
) =( b fнеlimxобходимо и дос т ат оч но, ч т обы |
||||||||||||||
функция α |
= |
|
) −(bx(былx) fабе с конеч но мал ойпри x → а . |
|
|
|||||||||||

16
2. Ал гебраич е с кая с умма и произве дение конеч ного ч ис л а бес конеч но мал ы хфункций при x → а , ат акж е произведение бес конеч но мал ой функции наогранич е нную функцию явл яю т с я бе с конеч но мал ыми функциями при x → а .
Ср а в нение беск онечно м а л ы хи беск онечно бол ьш ихфунк ций .
П ус т ь функции α (x) и β (x) , заданные дл я однихи т ех ж е знач е ний аргуме нт ов, явл яю т с я бе с конеч но мал ыми в т оч ке x = а , т огда:
1. |
Е с л и lim |
α(x) |
|
= 0 , т о α (x) |
– бес конеч но мал ая бол ее выс окого порядка, |
||
β (x) |
|||||||
|
x→a |
|
|
||||
ч ем β (x) . |
|
|
|
|
|
||
2. |
Е с л и lim |
α(x) |
|
= А ¹ 0 , где А – ч ис л о, т о α (x) и β (x) – бе с конеч но мал ы е |
|||
β (x) |
|||||||
|
x→a |
|
|
||||
одного порядка. |
|
|
|||||
3. |
Е с л и lim |
α(x) |
|
= 1, т о α (x) |
и β (x) – эквивал е нт ны е бе с конеч но мал ы е в |
||
β (x) |
|||||||
|
x→a |
|
|
||||
т оч ке а , обознач ает с я α(x) ~ β (x).
|
|
|
|
|
|
Пер в ы й |
за м еча тел ьны й |
пр едел |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
lim |
sin x |
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В тор ой |
за м еча тел ьны й |
пр едел |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
æ |
|
1 ö |
n |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
lim(1+ x)x = e ил и |
ç1 + |
lim÷ = e |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
n→∞è |
|
n ø |
|
|
|
|
|
|
|
||
|
|
§4. Пр им ер ы р еш ения за да чпо тем е «Пр едел функ ции» |
|
|
|
|||||||||||||||||||
I. Пр остей ш ие сл уча и. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1-й |
сл уча й . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ес л и пре дел ь ное знач ение аргуме нт апринадл еж ит |
обл ас т и определ е ния |
|
||||||||||||||||||||||
функции, |
т о выч ис л е ние |
предел а функции с водит с я к подс т ановке |
пре - |
|
||||||||||||||||||||
дел ь ного знач ения аргуме нт ав функцию , т . е. |
x→a |
|
= a)f, ( fÎx )(a(f ).Dlim |
|
||||||||||||||||||||
1. |
(x3 |
2 |
2 |
3 |
2 |
|
|
x |
x→ |
x |
|
|
x =17+x |
5+ x 16- = 12+ 8 +5 |
lim |
|||||||||
2 |
|
x −1 |
|
|
3 − 1 |
|
2 |
x→ x→2 |
|
x→ |
|
|
|
|||||||||||
2. lim |
|
= |
= 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x→3 |
|
3 + 2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2-й |
сл уча й . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ес л и аргуме нт |
с т ре мит с я к бес коне ч нос т и ил и к ч ис л у, кот орое не |
при- |
|
|||||||||||||||||||||
надл еж ит обл ас т и опреде л ения функции, т о возмож ны вариант ы : |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
lim ax = ¥ |
lim |
x |
= ¥ |
|
|
lim |
a |
= ¥ |
|
|
a |
= 0 |
lim |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 = ¥ |
|
x→∞ |
x→∞ a |
|
|
x→0 x |
|
|
x→∞ x |
|
|
|
|||||||||||
4. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x→0 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5. lim |
|
|
4 |
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
x→∞ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
II. Н еопр едел енностьв ида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В т ом с л уч ае, е с л и при подс т ановке в выраж е ние в ч ис л ит е л е и знаменат е - |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
л е |
выраж е ния пол уч ает с я нул ь , |
говорят , |
ч т о задананеопредел е ннос т ь |
0 |
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Выде л яю т с л е дую щ ие с л уч аи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
1-й |
|
|
сл уча й . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Е с л и под знаком предел ас т оит дробно-рационал ь ная функция, т о дл я т ого, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ч т обы |
|
рас крыт ь |
неопредел е ннос т ь |
0 |
|
, |
|
необходимо ч ис л ит е л ь |
и знамена- |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
т е л ь дроби разл ож ит ь намнож ит ел и и выпол нит ь необходимые преобразо- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вания. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
6. lim |
x2 −16 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
x→4 |
|
|
|
x − 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Убедимс я, ч т о пре де л функции нел ь зя найт и не пос редс т веннойподс т анов- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
кой. |
Д л я эт ого в ч ис л ит е л ь и знаме нат ел ь выраж ения |
подс т авл яем пре - |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
дел ь ное знач е ние аргумент а– 4, пол уч ае м неопреде л еннос т ь |
0 |
. Разл ож им |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||
ч ис л ит е л ь дроби намнож ит ел и, с ократ им дробь на x − 4 , в ре зул ьт ат е име - |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ем: |
|
|
|
|
|
|
|
x − |
|
|
|
x + |
) |
4 ( )(x 4= = 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
= |
|
0 |
|
= lim |
|
|
|
|
+) 4 |
|
|
|
( |
|
lim |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
0 |
|
|
x − 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x→4 |
|
|
|
|
|
x→4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Анал огич но реш аю т с я приме ры 7 и 8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
7. lim |
|
|
|
|
|
x − 2 |
= |
|
0 |
|
= lim |
|
|
|
x − 2 |
|
= lim |
|
|
1 |
|
= |
1 |
= 1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
2 |
|
x |
|
− 3x |
+ 2 |
|
|
|
0 |
|
2 |
|
− |
|
|
− ) 2 ( |
)(x −11 x1 |
x |
x→ |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→ x→2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
8. |
|
|
|
|
|
|
|
x2 + 6x + 8 |
|
|
|
|
0 |
|
|
|
|
|
|
|
x + x + ) 4 ( )( 2 |
x (+ ) 4 |
|
1 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
= |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
x3 + |
8 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
+x + |
|
|
|
|
|
|
6 2 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
) 4x− x −2→x x2 (−)( x2+ )(4 |
|
x − → |
|
→− |
||||||||||||||||||||||||||||||||||
2-й |
|
|
сл уча й . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Е с л и под знаком преде л ас т оит |
иррационал ь ное |
|
выраж е ние, т о дл я т ого, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ч т обы |
|
рас крыт ь |
неопредел е ннос т ь |
0 |
|
, |
|
необходимо ч ис л ит е л ь |
и знамена- |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
т е л ь |
дроби домнож ит ь на выраж е ние, |
с опряж енное иррационал ь ному, |
и |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
выпол нит ь необходимы е преобразования. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
) ( |
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
= x − 5 |
−xx4− 1 = + x2 − 1 −1 − 2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
иррационал ьное с опряж енное |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
9. lim |
1 − |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Выяс нив пе рвонач ал ь но, ч т о при указанном изме нении аргумент аданная функция пре дс т авл яе т от нош е ние двухбес конеч но мал ыхвел ич ин, преобразуе м зат ем дробь т ак, ч т обы с ократ ит ь е е намнож ит ел ь , с т ре мящ ийс я к
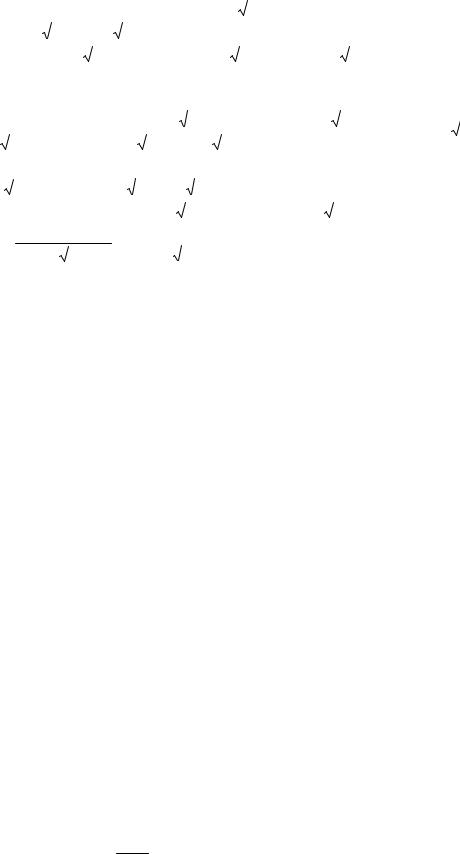
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
нул ю . Д л я эт ого унич т ож аем |
|
иррационал ь нос т ь |
в ч ис л ит ел е пут е м умно- |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ж е ния ч ис л ит е л я и знаменат е л я на1 + |
|
|
|
|
|
|
|
|
|
|
|
, зат ем с окращ аем дробь наx : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x + 1 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
( |
|
|
|
|
|
|
|
)( |
|
|
|
|
|
|
) 1+- 1+11- x - 1 |
|
|
|
|
- 1 |
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
= - |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
0 |
|
|
|
x (1 + x + 1) |
|
|
(1 |
+ |
|
|
|
|
+ 1) |
(1 |
+ x + 1) |
2x |
|
x |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
→0 |
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|||||
Анал огич но реш аю т с я приме ры 10 и 11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(2 + |
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(2 + |
|
|
|
|
) |
|
|
|
( |
|
|
) -4= +4 |
|
||||||||||
lim |
|
|
x |
|
|
|
= |
|
|
0 |
= lim |
|
|
|
|
|
|
x + 4 |
|
|
|
|
|
|
|
= lim |
|
|
x + 4 |
|
|
|
|
|
+ 2= -li |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
)( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
2 - x + 4 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x + 4) 2+- |
2+ 4 |
|
|
|
|
|
|
|
|
x→0 |
|
|
x→0 |
x→0 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 - x - 4 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
3x - x |
|
|
|
0 |
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ x) x x 3 x)(3x -( x3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
lim |
|
|
|
|
|
|
|
= |
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
||||||||||||||||||
|
|
x - 3 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→3 |
|
|
|
|
|
|
|
x→3 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
x + x) x |
|
|
x→3 |
|
|
|
|
|
|
|
|
|
|
|
)( 3 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 ( )(-3 |
|
|
x + x) x 3 ( |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
= lim |
|
|
|
x |
|
|
− x) |
(3 = - lim |
|
|
|
|
|
x |
|
|
|
= - |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
x→3 |
|
|
|
|
|
x + x) x 3 ( )( 3 x + x) |
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3-й |
сл уча й . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Е с л и под знаком предел ас т оит т ригономе т рич ес кое выраж ение, т о дл я т о- |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
го, |
ч т обы рас крыт ь |
|
неопреде л еннос т ь |
|
|
0 |
, |
не обходимо преобразоват ь |
вы - |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
0 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
раж е ние, ис пол ь зуя ос новны е т ригономет рич ес кие формул ы .
12. |
lim |
|
|
sin 2 x |
|
= |
|
0 |
|
= lim |
|
1 - cos2 x |
|
|
|
= |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
)( |
|
|
- + cos2xx+) |
cosx |
|
1 1 cos |
|
||||||||||||||||
|
x→0 1 - cos3 x |
|
|
|
|
x→0 ( |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
( − |
|
|
|
|
|
x)( + cos x) |
1 |
|
1 |
cos |
(1 + cos x) |
|
|
2 |
|
|
|||||||||
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
= |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
( |
|
|
|
|
|
)( |
|
|
|
|
|
cosx( |
+ |
|
|
|
|
|
|
|
|
|||||||
|
x→0 |
|
|
|
|
|
|
- + cos xx+) |
|
1x +1 coscosx) 13 cos |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
||||||
III. Пер в ы й |
за м еча тел ьны й |
пр едел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
sin x |
= lim |
x |
= 1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
3x sin |
|
|
|
|
|
|
|
|
x→0 |
x |
|
|
|
x→0 sin x |
|
|
|
|
|
|
|
|
|||||
13. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
|
|
|
|
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
14. |
lim |
|
|
x2 |
- 3 |
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
(x2 - 3) |
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
15. |
lim |
|
|
5x sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Умнож им ч ис л ит ел ь и знаменат е л ь дроби на5 , |
т .к. у функции |
5x sinаргу- |
||||||||||||||||||||||||||||||
мент 5x , дл я т ого ч т обы приме нит ь 1-й замеч ат е л ь ны й предел , необходимо, ч т обы в знаме нат ел е т акж е был о 5x :
|
|
5x5sin |
|
|
5x sin |
= 55× . 1= |
|
|||
lim |
|
|
|
5lim |
|
|
|
= |
||
|
5x |
|
|
5x |
||||||
x→0 |
|
|
x→0 |
|
|
|
||||
16. lim |
|
x − |
3x sin |
6 sin |
|
|||||
|
|
|
|
|
= |
|
|
|
||
|
|
x |
|
|
|
|
|
|||
x→0 |
|
|
|
|
|
|
|
|
||
ис пол ь зуе м формул у a −c b = ac - bc , дал ее ре ш аем анал огич но примеру 15.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6x sin |
|
|
|
|
|
|
|
|
|
|
|
3x sin |
|
|
|
|
6x6sin |
|
|
|
|
|
|
3x3sin |
|
|
|
|
|
|
|
|
|
|
6x sin |
|
|
|
|
|
|
|
|
|
|
|
3x sin |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
lim |
|
|
|
|
|
|
|
|
|
3 |
|
lim |
|
|
|
|
|
|
|
|
|
|
= 63 - 3 = |
× - |
|||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
6x |
|
|
|
|
|
|
|
|
3x |
|
|
|
|
|
6x |
|
|
3x |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
x→ 0 |
x→ 0 |
||||||||||||||||||||||||||||||||||||||||||
17. lim |
|
|
|
|
3x |
|
|
tg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x sin |
|
|
|
|
|
|
|
|
3x3sin |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
= 3 |
|
|
|
|
|
|
|
|
=× |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
x cos 3x |
|
|
|
3x |
|
|
|
|
|
|
cos 3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
x→0 x →0 |
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
18. lim |
|
|
|
|
|
2x sin |
|
|
|
|
|
|
|
|
|
× x × |
|
× 2x si2n2 |
|
3 |
|
|
|
|
|
|
3x sin |
|
|
|
2x |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
lim |
|
|
|
= |
|
= |
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
sin 3x |
2 |
|
|
x |
3×× sin× 3x |
3 |
|
|
3x |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
sin 2x |
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
x→0 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
IV. Н еопр едел енностьв ида |
¥ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Е с л и при x → ∞ ил и x → a функция |
|
f (x) пре дс т авл яе т от нош ение двухбе с - |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
конеч но бол ь ш ихвел ич ин |
¥ |
, т о необходимо ч ис л ит ел ь и знаме нат ел ь |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
дроби разде л ит ь нанаивыс ш ую с т е пень переменой x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
19. lim |
|
3x2 |
|
-1 |
|
|
= |
|
¥ |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ 2x |
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x→∞ 5x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
дел им ч ис л ит е л ь и знаменат е л ь дроби наx2 , пол уч им: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3 - |
|
|
|
|
|
|
|
|
3 - 0 |
|
|
|
|
|
3 |
, т .к. при x → ∞ вел ич ины |
1 |
|
|
|
|
|
|
|
2 явл яю т с я бес коне ч - |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= lim |
x2 |
= |
= |
|
|
|
и |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
5 + 0 |
|
5 |
x2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x→∞ |
5 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
но мал ыми. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 öù20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é |
|
3 æ |
|
|
|
|
|
|
|
|
|
|
|
|
60 æ |
|
|
2 ö20 |
|
|
|
|
|
æ |
|
|
|
|
2 ö20 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
( 3 - |
|
|
)20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
êx |
ç1- |
|
|
|
|
|
|
÷ú |
|
|
|
|
|
|
|
|
|
x |
|
|
ç1- |
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
ç1- |
|
|
|
|
|
÷ |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
20. lim |
|
x |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
= lim |
ë |
|
è |
|
|
|
|
|
|
|
øû |
|
|
|
|
= lim |
|
|
|
|
è |
|
|
|
|
ø |
|
|
= lim |
è |
|
|
|
|
ø |
|
= 1 |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
(x - 2)60 |
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
öù60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
2 ö60 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
é |
æ |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
x |
60 |
æ |
|
2 |
|
ö |
|
|
x x |
|
|
∞ →æ |
|
|
|
|
|
x ∞ → |
→∞ |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
êxç1- |
|
|
|
|
÷ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç1 |
- |
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
ç1 |
- |
|
|
|
÷ |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
è |
|
|
|
|
|
øû |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
ø |
|
|
|
|
|
|
|
|
è |
|
|
|
|
ø |
|
|
|
|
|||||||||||||||||||||||
В ч ис л ит е л е зас кобки вынес е м x3 , ав знаменат е л е |
|
x ; с ократ им наx60 |
и |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
уч т ем, ч т о при x → ∞ вел ич ины |
|
|
2 |
|
|
и |
2 |
|
явл яю т с я бе с конеч но мал ыми. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x3 |
|
x |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
1 ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç1 |
- |
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
x2 -1 |
|
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 - x2 |
|
|
|
|
|
1 - 0 |
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
21. lim |
|
|
|
|
|
|
|
= |
|
|
|
= lim |
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
x2 ø |
|
= lim |
|
|
|
|
|
= |
|
|
= |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
4x |
2 |
|
+ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 æ |
|
|
|
|
|
3 ö |
|
|
x x ∞ → |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
x |
+ 02 12 |
|
|
|
|
→∞ |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ → |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x |
|
|
ç1 + |
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
2x |
1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
V. Н еопр едел енностьв ида 1∞ . В тор ой |
за м еча тел ьны й |
пр едел |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
1 |
ön |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1+ xlim)x |
= e ил и |
|
|
|
|
|
|
ç1 |
+ |
lim÷ |
|
= e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞è |
|
|
|
n |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
22. x→0( + 3x)1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
убе дивш ис ь , ч т о при указанном изменении аргумент аимее м неопреде л ен- |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
нос т ь |
вида 1∞ , дал ее |
|
преобразуем |
|
функцию |
|
т ак, |
ч т обы |
|
ис пол ь зоват ь 2-й |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
замеч ат е л ь ны й преде л . Д л я эт ого домнож им ч ис л ит ел ь и знаменат е л ь с т е - |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
пени на3 и вос пол ь зуемс я с войс т вом пре дел а |
x→a |
[ |
|
|
( |
|
|
)]n = [lim |
|
|
(x)]fn : |
|
limf x |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

20
¥ |
|
|
|
|
|
|
|
|
|
|
1×3 |
|
|
|
æ |
|
|
|
|
|
|
|
1 |
|
|
ö3 |
æ |
|
|
|
|
|
|
|
1 |
ö3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x×3 |
|
|
|
|
|
|
|
|
3x |
|
|
|
|
|
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
( |
|
|
|
|
|
) |
|
|
ç( |
|
+ |
|
) |
÷= = ç |
|
|
(+ +=3 |
|
÷ lim= e |
|
|
|
|
|
|
x 3x |
1 |
|
|
|
lim |
|
x |
3 11 |
lim |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)=1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
x®0 |
|
|
|
|
|
|
|
|
|
x®0è |
|
|
|
|
|
|
|
|
|
|
|
ø |
è x |
®0 |
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
В примере № 23 ч ис л ит е л ь и знаменат ел ь с т е пени домнож ает с я на-1. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
× - |
) 11 ( |
|
|
|
|
|
|
çæ( |
|
|
|
|
1 |
(÷ö |
-1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
23. |
( |
|
|
) |
|
|
|
|
|
¥ |
|
|
( |
|
|
|
|
|
|
) |
|
|
|
( |
|
) |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
-x)+)- |
|
|
1== |
|
limx |
-x+ ) |
( = 1 |
lim-x+ ) |
||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
x |
|
|
x× -( ) |
|
|
|
|
|
|
|
x |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
x®0 |
|
|
|
|
|
|
|
|
|
|
|
|
x®0 |
|
|
|
|
|
|
|
|
|
|
|
|
x®0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x®0 |
è |
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
||||||
|
æ |
|
|
|
|
|
|
|
|
|
- |
1 |
ö-1 |
|
|
|
-1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
ç |
=( |
|
|
|
|
-x)+) |
x(÷ |
1= elim= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
è x®0 |
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В примере № 24 ис пол ь зует с я формул аb |
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
a |
= a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1×5 |
æ |
|
|
|
|
|
|
|
|
|
1 |
|
|
ö5 |
|
æ |
|
|
|
|
|
|
|
1 |
ö5 |
5 |
|
|
|
|
|||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x×5 |
|
|
|
|
|
|
|
|
5 x |
|
|
|
|
|
|
|
5 x |
|
|
|
|
||||||||||||||||||
24. |
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
) |
|
|
|
( |
) |
ç( + |
|
|
|
) |
÷= = |
ç |
|
(+ + 5 |
|
|
|
|
=x 5 1 |
lim |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)1= ÷ lim= e+ + |
|||||||||||||||||||||||||||||||||||||||
|
x 0 |
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
x®®0 |
|
|
|
|
|
®x®0è |
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
è x®0 |
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|||||||||||||
В примере № 25 ис пол ь зует с я формул а x |
n |
|
æ 1 |
ö-n |
, дал е е выде л яет с я цел ая |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= ç |
|
|
÷ |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ч ас т ь . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è x |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
æ n |
|
|
ön |
|
¥ |
|
|
|
æ n + 1ö-n |
|
|
æ |
|
1 ö-n |
|
|
æ |
|
|
|
|
æ |
|
|
|
|
1 ön |
ö-1 |
|
|
|
-1 |
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||
25. |
lim |
ç |
|
|
|
÷ |
|
=1 |
|
= lim |
ç |
|
|
|
÷ |
|
|
|
|
= |
n®¥ |
ç1 |
+ |
|
lim÷ |
|
= |
ç |
|
|
|
|
ç1 |
+ |
|
lim÷ |
÷ |
= e |
|
|
= |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
n®¥ |
è n + |
1ø |
|
|
|
|
|
n®¥ |
è |
|
|
|
ø |
|
|
|
|
|
è |
ø |
|
|
|
çn®¥ |
è |
|
|
|
nn ø |
|
÷ |
|
|
|
|
|
|
|
en |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
§5. Н епр ер ы в ностьфунк ции. Т очк и р а зр ы в а . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Опр едел ение. Ф ункция непреры вна в т оч ке |
x0 , ес л и: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
1. Ф |
ункция опре дел енав некот орой окре с т нос т и т оч ки |
x0 , вкл ю ч ая с аму |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
эт у т оч ку. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. В т оч ке с ущ ес т вует предел , и он равен знач ению функции в эт ойт оч ке, |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
т .е . |
x®x0 |
= |
|
x0 )f . (f |
x |
|
) |
( |
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
В прот ивном с л уч ае функция ра зры вна ил и имее т разрыв в т оч ке |
x0 . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
А р ифм етическ ие дей ств ия на днепр ер ы в ны м и функ циям и |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
П ус т ь функции |
|
|
f (x) и |
g (x) |
не прерывны в т оч ке x0 , |
|
т огдафункции |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
f (x) ± g (x) , f (x)× g (x) |
|
и |
f (x) |
, |
при ус л овии |
|
|
g (x) ¹ 0 , |
т акж е не прерывны в |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
g (x) |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
эт ойт оч ке.
Вс е ос новные эл е ме нт арные функции непрерывны т ам, где они определ е ны .
Опр едел ение. Е с л и функция f (x) не явл яет с я непрерывнойв т оч ке x0 , т о
говорят , ч т о в т оч ке x0 |
функция f (x) разрывна, ат оч каx0 называет с я то ч- |
ко й ра зры ва функции |
f (x). |
