T
 (xt )2
(xt )2
t0
- при параметрическом задании кривой,
производные от х и у по t непрерывны на [t0,T].
Вычисление объема тела вращения
Если Т – тело вращения, полученное от вращения вокруг ОХ криволинейной трапеции, ограниченной прямыми х=а; х=b; у=0 и у=f(x),
то это тело регулярно, причем
Практическая часть:
1. Вычислить объем тела, образованного вращением вокруг оси ОХ
фигуры, ограниченной кривыми
Решение: Для построения чертежа, выясним, что это
|
|
2 |
|
|
2 |
|
2 |
|
2 |
|
2 |
|
x |
2 |
y 3 |
1 x |
, |
y |
9 9x |
, 9x |
y |
9, |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
эллипса с полуосями а=1, b=3.
x |
1 y, x |
2 |
1 y, |
y 1 x |
2 |
. |
|
|
Это уравнение параболы с вершиной в
точке (0, 1), ветви параболы направлены вниз. Сделаем чертеж:
3
2
1
1
2
3
Объем тела вращения найдем по формуле b
V [y22 (x) y12 (x)]dx,
a
9x 2 (1 x 2 )2 ]dx
x5 )1 (8 7 1) 5 0 3 5
|
|
1 |
|
|
|
|
|
|
|
|
|
(8 7x |
2 |
x |
4 |
)dx |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
82 |
17,174 (куб. ед) |
|
15 |
|
|
|
|
|
|
|
Ответ: Объем тела вращения равен
2. Вычислить длину дуги полукубической параболы y |
(x 2)3 от |
точки А(2,0) до точки В(6,8). |
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
Сделаем чертеж |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Длину дуги линии, заданной параметрически, найдем по формуле:
|
|
|
|
f '(x) |
|
Найдем |
|
|
|
|
|
|
1 ( f |
|
Получим |
|
|
|
3 |
6 |
|
14 |
|
L |
|
x |
|
2 |
9 |
|
|
2 |
|
|
|
|
|
|
|
(10 10 1) 9,073 |
((x 2) |
3 / 2 |
)' |
3 |
|
1 / 2 |
; |
|
|
|
|
|
|
|
|
|
|
|
2 |
(x 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
'(x)) |
2 |
1 |
|
9 |
(x |
2) |
9x 14 |
|
9 |
x |
7 |
|
9 |
(x |
14 |
). |
|
|
|
|
|
|
|
|
|
4 |
4 |
|
4 |
2 |
4 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
(x |
14 |
) |
3 / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
14 |
|
|
3 |
9 |
6 |
|
40 |
|
|
|
4 |
|
|
|
dx |
(x |
1 / 2 |
dx |
|
|
( |
) |
3 / 2 |
( |
) |
3 / 2 |
|
2 |
9 |
) |
2 |
3/ 2 |
2 |
9 |
|
9 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(лин.ед.)
Ответ: Длина дуги равна 278 (10
 10 1) 9,073 (лин. ед.).
10 1) 9,073 (лин. ед.).
3. Вычислить длину дуги кардиоиды r=2(1-cos ). Решение:
Сделаем чертеж:
90 |
|
|
|
135 |
|
45 |
180 |
|
|
0 |
0 1 |
2 |
3 |
4 |
225 |
|
315 |
270 |
|
|
|
Длина дуги в полярной системе находится по формуле:
2
L 
 r( )2 r'( )2 d .
r( )2 r'( )2 d .
1
Найдем r ( )=2sin ; r( )2+r ( )2=4(1-cos )2+4sin2 =4-8cos +4cos2 +4sin2 =8(1-cos )
|
|
|
|
2 |
|
|
cos |
|
2 |
|
|
|
|
|
|
4 sin |
2 |
. |
|
|
|
2 |
|
|
|
|
|
|
|
d 2 |
1 |
4 4 8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
2 sin |
|
|
|
|
|
2 |
L |
|
2 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Ответ: Длина дуги кардиоиды равна 8 (ед.).
4. Вычислить объем тела, образованного вращением вокруг оси ОХ
фигуры, ограниченной параболами y x 2 , y 
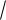 x. Решение:
x. Решение:
Сделаем чертеж:
1
0.5
0.5
1
Объем тела вращения найдем по формуле
|
b |
|
|
|
V |
|
[y2 |
(x) y2 |
(x)]dx, |
|
|
2 |
1 |
|
|
a |
|
|
|
1 |
x 2 |
|
x5 |
|
|
|
|
|
|
|
|
|
V [x x 4 ]dx ( |
|
1 |
( |
1 |
|
1 |
) |
3 |
. |
|
|
) |
0 |
|
|
|
|
2 |
5 |
2 |
5 |
10 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: Объем тела вращения равен
5. Вычислить длину дуги полукубической параболы |
y |
(x 2) |
3 |
|
точки А(2,0) до точки В(6,8).
Задания для самосоятельного решения:
1. Вычислить длину астроиды x=cos3t, y=sin3t (0 t 2 ).
2.Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной кривыми у=х2, х=у.
Несобственные интегралы
1.Исследование на сходимость несобственного интеграла первого рода.
2.Исследование на сходимость несобственного интеграла второго рода
Теоретическая часть:
Несобственные интегралы
Пусть f(x)
b
lim f (x)dx b a
определена на [а, +∞) и для любого b≥a
называется несобственным интегралом
первого рода от f(x). Если этот предел конечен, то интеграл называется сходящимся, если бесконечен или вовсе не существует – расходящимся.
Обозначение таких интегралов:
Определение: Пусть f(x) определена и интегрируема в [a, b-ε],
|
|
b ,b .lim |
b |
|
|
b a |
и неограниченна в |
|
f (x)dx |
называется |
|
0 |
|
|
|
|
a |
|
|
несобственным интегралом второго рода. Интеграл называется сходящимся, если этот предел конечен, и расходящимся, если предел
b
бесконечен или не существует. Обозначается: f (x)dx.
a
Практическая часть:
1. Вычислите несобственные интегралы.
Решение:
Подынтегральная функция непрерывна в промежутке [1; ). По определению несобственного интеграла с бесконечным пределом интегрирования
|
|
|
|
N |
|
1 |
|
|
2 |
3 |
N |
|
|
|
|
2 |
|
dx |
|
|
|
|
|
х |
|
|
3 |
|
3 |
|
|
lim |
х |
3 dx |
lim |
2 |
|
|
|
|
lim |
|
3 |
|
|
|
|
|
|
|
1 |
|
N |
1 . |
1 |
х |
|
N |
1 |
|
|
N |
|
3 |
|
2 N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, несобственный интеграл расходится.
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
Подынтегральная функция терпит разрыв в точке х=2/3. По |
определению |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
dx |
lim |
|
dx |
|
1 |
lim ln | 3x 2 | |
|
|
|
|
|
|
|
|
|
3x 2 |
3x 2 |
3 |
2 |
|
|
0 |
|
0 |
3 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
lim |
(ln 4 ln( 3 )) . |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
То есть интеграл расходится.
2.Вычислите несобственные интегралы.
dx
a)1 (3 4x) 2
Подынтегральная функция непрерывна в промежутке [1; ). По определению несобственного интеграла с бесконечным пределом интегрирования
Решение:
|
dx |
|
|
N |
dx |
|
|
|
lim |
|
|
|
|
|
|
(3 4x) |
2 |
(3 4x) |
2 |
1 |
|
N |
1 |
|
|
|
|
|
|
|
Таким образом, несобственный интеграл сходится и равен
0dx
b)1 x 1
Решение:
Подынтегральная функция терпит разрыв в точке х=-1. По определению
|
0 |
dx |
|
0 |
dx |
|
0 |
|
|
|
lim |
|
lim ln | x 1 | |
|
|
x 1 |
x 1 |
1 |
|
1 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
lim (ln 1 ln ) . |
|
|
|
|
0 |
|
|
|
|
|
|
То есть интеграл расходится.
3. Вычислите несобственные интегралы.
|
dx |
1 |
dx |
|
|
|
|
|
|
|
|
|
dx |
a) |
b) |
c) |
|
|
|
|
|
|
|
|
2x |
3 |
3 |
|
|
2 |
|
2 |
0 |
( 1 x ) |
|
1 |
x |
|
2x 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задания для самосоятельного решения:
Вычислить несобственные интегралы или доказать их расходимость:
Двойной интеграл, его вычисление
1.Переход от двойного интеграла к повторному.
2.Смена порядка интегрирования.
3.Вычисление повторных интегралов.
Теоретическая часть:
Определение: Двумерной интегральной суммой от данной функции f(x, y), распространённой на область S, называется сумма произведений площадей элементарных областей Si на значение
n |
|
|
|
|
( f (xi , yi )P( Si)) |
i 1 |
|
|
|
|
i |
i |
)P( Si) |
|
f (x |
, y |
|
f |
|
|
|
S |
|
разбиения S, ни от выбора точек (xi , yi ) Si.
b
Принципиальной разницы между и нет. Различия связанны с
a S
b
изменением размерности рабочего пространства, поэтому те свойства ,
a
которые не зависят от размеренности пространства, переносятся на случай двойного интеграла без изменений.
Если область D стандартна относительно оси ОХ, т.е. c ≤ y ≤ d,
x |
( y), |
то по аналогии получим: |
|
|
2 |
|
|
|
|
|
|
d |
x |
( y ) |
|
|
|
|
2 |
|
|
|
f (x, y)dxdy dy |
|
f (x, y)dx. |
|
|
D |
c |
x |
( y ) |
|
|
|
|
1 |
|
|
Если область D нестандартная, то её разбивают на конечное число |
областей |
S1, S2 ,..., Sn стандартных относительно осей координат Ох и Oy и на |
основании свойств пределов полагают
|
|
|
... |
D |
s |
s |
2 |
s |
n |
|
1 |
|
|
Двойной интеграл в полярных координатах. |
f (x, y)dxdy f (x, y)dS |
|
|
S |
S |
|
|
|
|
Желаем перейти к полярным координатам r и φ, полагая x = cosφ; y = rsin φ. Область интегрирования S разобьём на элементарные области Sij с
помощью координатных линий |
r |
обозначения |
r |
j |
r |
j 1 |
; |
j |
|
i 1 |
|
i |
|
|
|
|
|
rj (окружности) и j (лучи). Введём
. Т.к. Sij с точностью до б.м. более
высокого порядка малости относительно их площади |
как прямоугольники с измерениями |
r |
|
и r |
j |
P S |
j |
i |
|
|
можно рассматривать |
ij |
r |
|
r |
. |
Область |
j |
i |
j |
|
неправильной формы, примыкающая к границе проигнорируем, т.к. при
измельчении разбиения их суммарная площадь стремиться к нулю. Выберем |
M ij Sij - где M ij - вершина области Sij |
с координатами |
M |
ij |
r |
, |
. |
|
j |
i |
|
в ПДСК xij |
rj cos i , yij |
rj |
sin i f (xij , yij ) f |
rj |
cos i ; rj sin i |
f (x, y)dxdy lim , |
не |
зависит от добавления |
слагаемых |
S |
i 1... n |
1...n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 0
– двумерный элемент площади в полярных координатах.
Для вычисления этого двойного интеграла заменим его повторным.
Пусть S: |
r r , |
|
|
|
|
, r |
где |
r |
и |
r - однозначные, |
1 |
2 |
|
1 |
|
2 |
непрерывной функции на [α,β]. Тогда по аналогии с прямоугольными координатами имеем:
|
|
|
|
r |
|
|
|
F r, d dr |
|
|
2 |
|
F r, dr, |
|
d |
|
где F(r,φ) = rf(rCosφ,rSinφ). |
|
|
|
|
S |
|
|
|
r |
|
|
|
|
|
1 |
|
|
|
Интеграл Эйлера-Пуассона.
I |
|
x2 |
dx ~ I |
|
y2 |
dy I |
|
e |
x2 |
dxdy, |
e |
e |
|
|
|
|
|
|
2 |
|
y2 |
|
0 |
|
|
0 |
|
|
|
S |
|
|
Перейдём к полярным координатам:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
1 |
|
|
|
I |
2 |
e |
r |
rd dr |
|
d re |
r |
dr |
0 |
|
|
e |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по свойству т.к. |
I 2 |
f x, y dxdy ~ I e x |
dx |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
x |
2 |
dx 2 |
|
e |
x |
2 |
dx |
|
|
|
. |
|
|
|
|
|
|
|
|
В силу чётности имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Практическая часть:
1. Вычислить повторный интеграл
Сначала вычислим внутренний интеграл по формуле НьютонаЛейбница. Его результат будет подынтегральной функцией для внешнего интеграла.
2. Изменить порядок интегрирования в повторном интеграле
3.Изменить порядок интегрирования
4. Поменять порядок интегрирования
5. Вычислить повторный интеграл
6. |
Вычислить двойной |
интеграл |
, где D- |
прямоугольник 0≤x≤2, 0≤y≤1 |
|
|
7. Вычислить интеграл |
,где область D параболический |
сегмент, ограниченный параболой 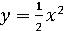 и прямой y=x.
и прямой y=x.
Задания для самосоятельного решения:
1.Поменять порядок интегрирования
2.Поменять порядок интегрирования
3.Вычислить двойной интеграл
по области D, ограниченной прямыми y=2x-3, y=2x+5, y=-x+7, y=-x-1
4. Вычислить двойной интеграл
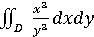 , где D ограничена линиями x=2, y=x,
, где D ограничена линиями x=2, y=x, 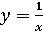
5. Вычислить двойной интеграл 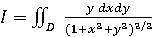 ,где D-квадрат
,где D-квадрат
0≤x≤1, 0≤y≤1
6. |
, если D: 0≤x≤ , 0≤y≤2 |
7. |
, где D ограничена линиями x=0, y =0, x=π |
Методы вычисления двойного интеграла
1.Вычисление повторных интегралов.
2.Замена переменных в двойном интеграле
Теоретическая часть:
Пусть:
f (x, y)dxdy; x x , y y ,

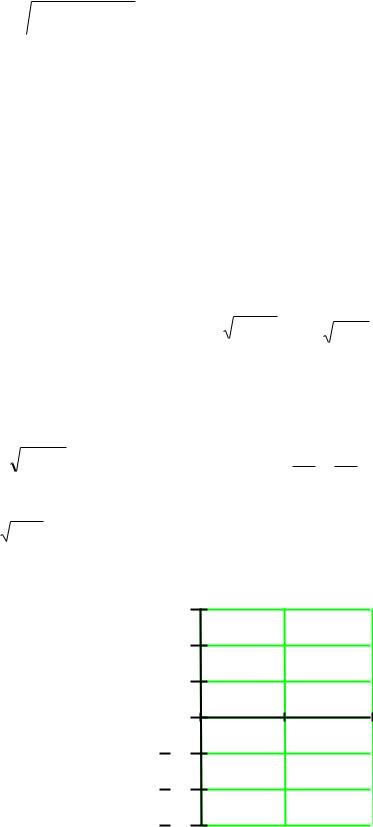
 (xt )2
(xt )2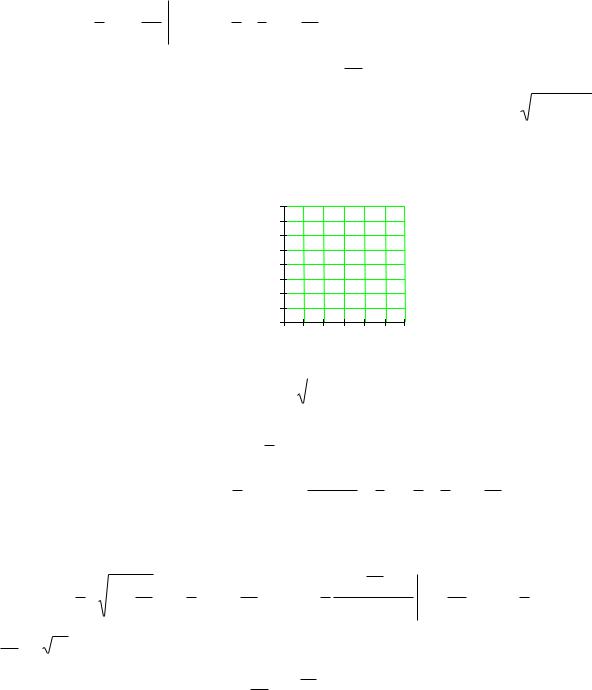
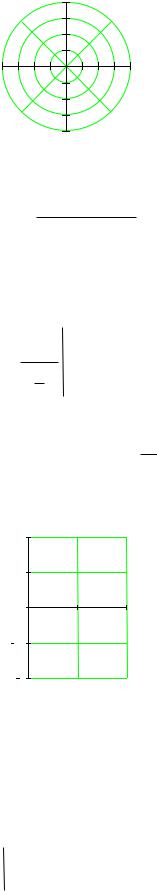

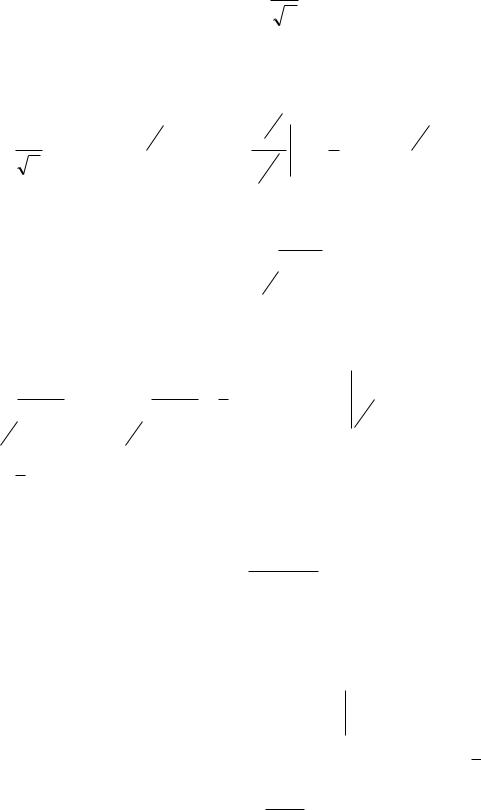
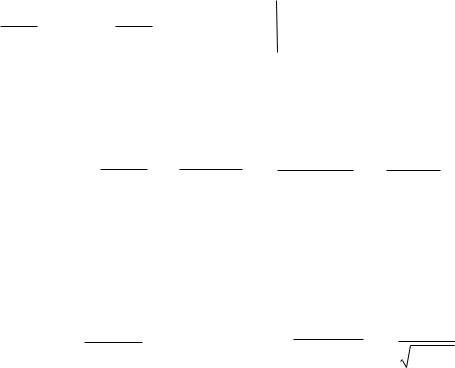

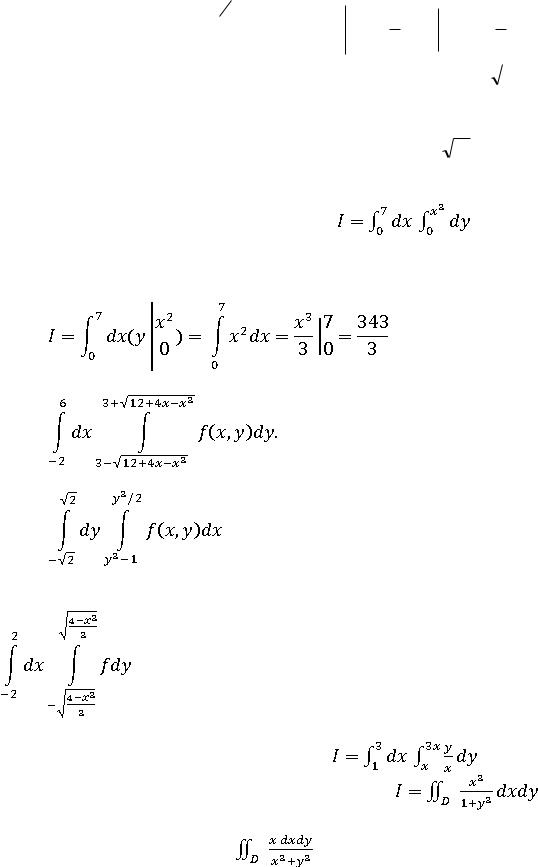
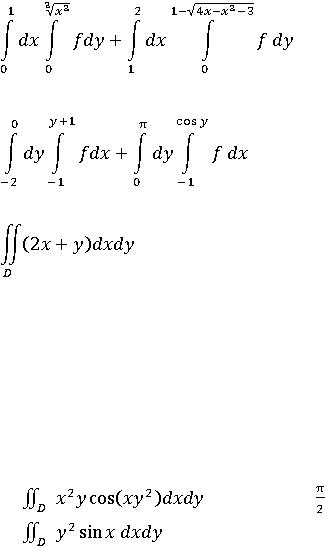




 r( )
r( )
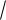
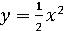 и прямой y=x.
и прямой y=x.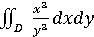 , где D ограничена линиями x=2, y=x,
, где D ограничена линиями x=2, y=x, 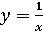
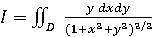 ,где D-квадрат
,где D-квадрат