
лекции по эконометрике
.pdf
Var(~y) 1 6 ~yt2 yt 2 91940,5 89510 2430,5.
6 t 1
5. Найдём коэффициент автокорреляции r(τ) исходного временного ряда для лага: =1.
7
yt 213 171 ... 351 2014;
t 1
7
yt2 2132 1712 ... 3512 609506;
t 1
7
yt 171 291 ... 361 2162;
t 1
7
yt2 1712 2192 ... 3612 694458;
t 1
7
yt yt 213 171 171 291 ... 351 361 642583;
t 1 |
|
|
|
|
|
||
По формуле (37) |
|
|
|
|
|
||
r(1) |
|
7 642583 2014 2162 |
|
|
0,725. |
||
|
|
|
|
|
|
||
|
|
7 609506 2014 2 |
|
7 694458 |
2162 2 |
||
Коэффициент автокорреляции для лага =2 вычисляется аналогично по шести парам на-
блюдений yt и yt 2 , (t=1,2,…,6) r(2)=0.842.
Вопросы к теме:
1.Дайте определение временного ряда.
2.Напишите общую модель временного ряда и назовите составляющие ее компоненты.
3.Что такое временной лаг?
4.Какой временный ряд называется строго стационарным?
5.Как определяется коэффициент автокорреляции и что он характеризует?
6.Как производится сглаживание временного ряда с помощью скользящей средней?
7.Как определяются цепные абсолютные приросты и цепные коэффициенты роста временно-
го ряда?
8.В каких случаях для описания временного тренда предпочтительнее использовать:
а) линейную функцию?
б) квадратичную функцию?
в) экспоненциальную функцию.
9. В каких случаях для описания временного тренда предпочтительнее использовать авторегрессионную модель(AR-модель)?
Лекция 10. ИСПОЛЬЗОВАНИЕ СПЕЦИАЛЬНЫХ ТИПОВ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ
10.1.Замещающие переменные и их использование
вэконометрических моделях
При работе с конкретным статистическим материалом часто встречаются ситуации осложняющие формулирование и проверку зависимостей между исследуемыми переменными величинами. Например, Вы не можете найти данные по переменной, которую хотели бы включить в уравнение регрессии. Или некоторая переменная имеет такое расплывчатое определение, что её невозможно измерить (социально-экономическое положение, качество образования и т.д.). Другие переменные могут быть измерены, но их измерение может оказаться настолько сложным, что сама мысль об этом кажется вам не заслуживающей внимания (исследование цвета кожи сотрудников фирмы).
Независимо от причины обычно бывает полезно вместо отсутствующей переменной включить
вуравнение регрессии ее заменитель (proxy), а не пренебрегать ею совершенно.
Вкачестве показателя общего социально-экономического положения можно использовать его заменительпоказатель дохода, вместо качества образования - отношение числа преподавателей в этом университете к числу студентов или расходы на обучение одного студента и т.д.
Примеры.
1. Функция Кобба-Дугласа с переменной , характеризующей технический прогресс: y=AkαL1-α.
3. |
Если считать А=А(t), где t-время, то А - показатель технического прогресса. |
|
Функция спроса потребителя (Энгеля): |
|
|
|
y=Axb1pb2, |
(38) |
где х - располагаемый личный доход; р - относительная цена товара.
Допустим, что мы не имеем данных о располагаемом личном доходе потребителей, либо они недостоверны, так как экономика «полутеневая».
Интересно, что очень похожие результаты дает замещение переменной х на переменную t,
т.е. на временной тренд. |
|
Например, после логарифмирования: |
|
log y=log А+b1log x+b2log p |
|
эту модель меняем на: |
|
log y=log А+b1t+b2log p. |
(39) |
Практика показывает, что в полутеневых случаях модель (39) даёт лучшее согласование со статистическим материалом, чем модель (38).
Рассмотренные выше примеры характеризуют один из распространенных в эконометрике приемов: замена одной из переменных на так называемый временной тренд. Однако использование замещения переменных ( в том числе и на временной тренд) может быть связано с риском получения неверных экономических оценок [3].
Еще одна проблема, которая возникает при выборе вида зависимости интересующей нас переменной от тех или иных объясняющих переменных, - это мультиколлиниарность.
Мультиколлиниарность возникает, когда в уравнении регрессии есть две или несколько объясняющих переменных, связанных между собой нестрогой линейной зависимостью. Эту проблему иногда решают замещением этих объясняющих переменных, на какую-либо новую переменную, либо
на временной тренд. |
|
|
Например: |
|
|
|
y=a1x1+a2x2+a3x3+u . |
(40) |
Если х1 |
и х2 явно коррелируют между собой, то можно заменить их на новую замещающую |
|
переменную х* |
и перейти к модели: |
|
|
y=a*x*+a3x3+u. |
(41) |
В случае, когда х1 и х2 явно зависят от времени, то вводится временной тренд: |
||
|
y=a*t+a3x3+u. |
(42) |
10.2. Инструментальные переменные
Что делать при существенном влиянии случайного члена «u» и, как следствие, в существенных расхождениях между у и ŷрасч.
Иногда помогает метод инструментальных переменных, который заключается в частичной замене непригодной объясняющей переменной на другую объясняющую, которая не коррелируется со случайным членом «u». Рассмотрим случай парной регрессии:
y=ao+a1x+u
Пусть х сильно коррелирует с u, но при больших выборках существует lim var(x)= x2.
n→∞

Пусть существует другая переменная z, которая коррелирует с х, но не коррелирует с u. То-
гда: |
|
y=bo+b1z+u* , |
(43) |
где b1=a1+ cov(z;u) ; bo-определяются по МНК.
cov(z;x)
Можно показать, что b1 более значим, чем а1 , если:
cov(z;u) <1. cov(z;x)
На практике выбор возможных инструменталных переменных для замены данной объясняющей переменной х бывает довольно ограниченным. Однако, если есть несколько разных вариантов замены переменной х другими инструментальными переменными, то выбрать из них наилучшую можно, используя двухшаговый метод наименьших квадратов.
Для этого составляется уравнение регрессии, где объясняемой переменной является предполагаемая инструментальная переменная z, а объясняющей переменная х. Полученные расчетные значения zˆ используются как значения объясняющей переменной в уравнении регрессии связывающем объясняемую переменную у с zˆ [3]
Метод нструментальных переменных используется также в случаях, когда имеется корреляция между случайным членом «u» и объясняемой переменной «у». Подробнее об этом см в лекции
12.
10.3. Лаговые́́́ переменные
Лаговой́́́ переменной называется объясняющая переменная X(t-p), которая зависит от времени, но влияние её на объясняемую переменную y(t) характеризуется некоторым запаздыванием (временным́лагом р).
Исследуя зависимость расходов населения на жилье, автомобили и другие достаточно крупные приобретения в зависимости от дохода, можно заметить, что эти расходы подвержены инерции и медленно согласуются с изменениями доходов и цен.
Потребители обычно не сразу адаптируются к изменению уровня своих доходов. Школьный учитель, зарплата которого неожиданно выросла на 15%, не сразу примет решение купить своей жене новый автомобиль. Должно пройти какое-то время «р» , за которое он возможно адаптируется к новому более высокому уровню жизни и начнет всерьез планировать крупные покупки. Регрессионная модель расходов на автомобили в зависимости от доходов может иметь следующий вид:
y(t)=a1x1(t-p) + a2x2(t) + a3 + u,
где x1(t-p) – лаговая переменная, характеризующая доходы потребителей на p (месяцев или лет) раньше данного времени t; x2(t) – переменная, характеризующая цену на автомобили в момент времени t.
Заметим, что переменная x2(t) также может быть снабжена определенным лагом, так как изменение цен в этом секторе обычно не сразу влияет на объем продаж.
Лаговые переменные используются в авторегрессионных моделях и в динамических моделях (см. лекции 13; 14). Иногда лаговые переменные используются как объясняемые, однако модели регрессии с такой структурой обладают рядом недостатков [3].
Вопросы к теме:
1. Приведите примеры использования замещающих переменных в экономических исследова-
ниях.
2.Как обнаружить мультиколлениарность между объясняющими переменными?
3.Каким образом можно выполнить замену коллениарных объясняющих переменных?
4.В чем суть метода инструментальных переменных?
Лекция 11. ФИКТИВНЫЕ ПЕРЕМЕННЫЕ И ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ С ИХ ИСПОЛЬЗОВАНИЕМ
Иногда случается, что тот фактор, который мы хотели бы ввести в регрессионную модель, не может быть измерен в числовой шкале. Например:
1.Исследуется зависимость между доходом и спросом на определенный продукт питания в такой стране, как Латвия, где 40% - русскоязычное население, 60% - латышское. Нужно выяснить, имеет ли существенное значение этническое различие?
2.Исследуется зависимость между продолжительностью образования и доходом. В выборке представлены и мужчины, и женщины. Нужно выяснить, влияет ли пол на эту зависимость?
Разумеется, можно в каждом из этих примеров разбить имеющуюся выборку на две части и выяснить, различаются ли коэффициенты регрессии?
Однако более эффективным является другой способ анализа. Можно ввести так называемую фиктивную переменную в уравнение регрессии, снабдив ее двумя возможными значениями. (Например: 0- если мужчина и 1 – если женщина). После того, как коэффициенты в уравнении регрессии найдены, оценивается значимость коэффициента при фиктивной переменной.
Пример. В 1974 году был нефтяной кризис. Цена на бензин резко увеличилась. Поэтому при анализе временного ряда, характеризующего спрос на автомобили в 1974 году, отмечается значительное падение спроса. Можно ли введя фиктивную переменную, «выровнять» функцию спроса на автомобили? (табл.4, рис.6).
Таблица 4
Анализ временного ряда
|
Годы |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
|
|
|
6 |
6 |
6 |
6 |
6 |
6 |
6 |
7 |
7 |
7 |
|
|
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
|
|
Спрос |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
|
|
(млрд. |
8 |
9 |
3 |
3 |
2 |
6 |
6 |
2 |
8 |
1 |
|
|
$) |
, |
, |
, |
, |
, |
, |
, |
, |
, |
, |
|
|
|
5 |
7 |
5 |
6 |
2 |
5 |
7 |
7 |
0 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Годы |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
|
|
|
7 |
7 |
7 |
7 |
7 |
7 |
7 |
8 |
8 |
8 |
|
|
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
|
|
Спрос |
3 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
|
(млрд. |
3 |
5 |
5 |
1 |
4 |
4 |
2 |
8 |
9 |
9 |
|
|
$) |
, |
, |
, |
, |
, |
, |
, |
, |
, |
, |
|
|
|
9 |
5 |
4 |
1 |
4 |
8 |
9 |
7 |
6 |
8 |
|
Рассмотрим уравнение регрессии в виде |
|
y=a0 + a1t + a2ф , |
|
(44) |
||||||||
|
|
|
|
|
|
|
|
|||||
где ф – фиктивная переменная, принимающая значение «0» для периода 1963-1973 годы и значение «1» для периода 1974-1983 годы.
y |
* |
|
* |
|
* |
|
36 |
|
|
|
|
|
|
|
|
34 |
|
|
|
|
|
* |
|
|
|
|
|
• |
* |
* |
|
||
32 |
|
|
|
• |
* |
|
|
|
30 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
28 |
|
|
|
• |
|
|
|
|
|
|
|
• |
|
|
|
||
|
|
|
|
|
• |
* |
|
|
|
|
|
|
|
|
|
|
|
26 |
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
• • • |
|
|
|
|
|
|
|
|
|
|
|
||
22 |
|
|
• |
|
|
|
|
|
|
• |
|
|
t |
||||
|
|
|
|
|
|
|
||
|
|
|
|
|||||
1 |
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
25 |
||||||
|
|
|
|
|
Рис.6. Спрос на автомобили с 1963-1982 гг. |
|
||
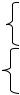
Вычислив коэффициенты уравнения (44) по МНК, получим: |
|
|
ŷ = 18,1 + 1,36∙t – 4,2∙ф , |
|
|
где |
|
|
0, если |
1 t 11 |
(45) |
ф = |
. |
|
1, если |
12 t 20 |
|
Проверка значимости коэффициента при ф с помощью |
t–критерия Стьюдента по- |
|
казывает, что этот коэффициент значим при α=5%. |
|
|
Если рассматриваемый качественный признак имеет несколько уровней k > 2 , то вводимая вместо него фиктивная переменная может быть снабжена таким же количеством различных значений. Например, если исследуется зависимость дохода от уровня образования, то этот уровень может иметь три различных градации : начальное, среднее, высшее. Соответствующую переменную ф можно снабдить следующими фиктивными значениями: 1 – начальное; 2 – среднее; 3 – высшее образование. Однако в этом случае возникают трудности содержательной интерпретации коэффициента регрессии при этой переменной. Кроме того, возможны трудности с выбором соответствующей модели регрессии. Она может оказаться нелинейной. Поэтому в таких случаях вводят несколько бинарных (т. е. имеющих только два значения) фиктивных переменных.
|
Например: |
|
|
|
|
y = a0 + a1x + a2ф1 + a3ф2 + u , |
(46) |
где ф1 |
= |
0, если высшее образование, |
|
|
|
1, в остальных случаях 1, |
|
ф2 |
= |
0, если среднее образование, |
|
1, в остальных случаях. |
|
||
|
|
|
|
Заметим, что количество бинарных фиктивных переменных должно быть на единицу меньше числа k – различных уровней качественного признака. В противном случае можно попасть в так называемую «dummy trap» (ловушка). Попадание в ловушку вызывает проблемы с определением коэффициентов уравнения регрессии [1].
На практике, довольно часто, фиктивные переменные используются в случаях, когда на изменение объясняемой переменной «у» оказывает сильное влияние сезонная компонента. Например, модель расходов населения на газ должна включать сезонную компоненту, потому что эти расходы неодинаковы в разное время года. Примерная модель временного ряда в этом случае может быть следующей:
у(t)=b0 + b1t + b2D1 + b3D2 + b4D3 + u ,
где D1,D2,D3 – бинарные фиктивные переменные, позволяющие учесть поквартальные изменения расходов населения на газ.
Количество фиктивных переменных, отражающих различные качественные признаки и включенных в уравнение регрессии может быть довольно большим. Однако необходимо соблюдать осторожность, чтобы в число исследуемых одновременно качественных признаков не были включены коррелирующие между собой признаки. Тогда мы столкнемся с уже описанным выше эффектом мультиколлинеарности.
Иногда возникает необходимость введения фиктивной переменной не в качестве объясняющей (независимой) переменной, но в качестве объясняемой (зависимой).
Например, при анализе причин разорения или банкротства банковских учреждений можно ввести фиктивную объясняемую переменную z c двумя значениями:
z0 = 0 – банкротство; z1 = 1 – в ост. случаях.
Вопросы к теме:
1.Сколько различных значений имеют фиктивные переменные?
2.Приведите примеры использования бинарных фиктивных переменных.
3.Как должны быть связаны между собой количество бинарных фиктивных переменных и количество значений моделируемого качественного признака?
4.Может ли бинарная фиктивная переменная быть объясняемой? Приведите пример.
Лекция 12. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ. КОСВЕННЫЙ И ДВУХШАГОВЫЙ МЕТОДЫ НАИМЕНЬШИХ КВАДРАТОВ
При анализе экономических ситуаций встречаются случаи, когда необходимо рассматривать системы уравнений, в которых одни и те же переменные в одних уравнениях выступают в роли объясняющих, а в других являются объясняемыми. Некоторые из этих переменных являются эндогенными, т.е. их значения формируются внутри модели, а некоторые могут быть экзогенными, т.е. их значения задаются заранее. Такие системы в эконометрике называются системами одновременных уравнений. Например, связь между спросом и предложением моделируется следующей системой:
Dt a1Pt a2I a3 e1, |
(47) |
St b1Pt b2 e2, |
|
Dt St,
где Pt – цена одной единицы товара; I – доход потребителя; e1, e2 – случайные члены.
Из четырех переменных в этой модели три: Dt, St, Pt – являются эндогенными, одна – I – является экзогенной.
Попытки определения параметров уравнения этой системы обычным методом наименьших квадратов, как правило, приводят к несостоятельным оценкам параметров. Дело в том, что эндоген-
ные переменные, выступая в роли объясняемых в первом и втором |
уравнениях системы (47), |
||||||||||
обычно коррелируют со случайными членами e1 |
и e2, т.е. |
нарушается четвертое условие Гаусса- |
|||||||||
Маркова (см. лекцию 3). |
|
|
|
|
|
|
|
|
|
|
|
Это проявляется в том, что третье равенство системы для расчетных значений Dt и St не вы- |
|||||||||||
полняется. |
|
|
|
|
|
|
|
|
|
|
|
В данном случае можно исключить из системы (47) переменные Dt |
и St |
и выразить экзоген- |
|||||||||
ную переменную I: |
|
+ b |
2 |
a |
|
|
e2 e1 |
|
|
|
|
1 |
1 |
3 |
+ |
. |
(48) |
|
|
||||
I = b |
a |
a2 |
|
a2 |
|
|
|||||
|
a2 |
Pt |
|
|
|
|
|
|
|
||
Экзогенная переменная I не связана со значениями случайных членов e1 |
и e2, и четвертое ус- |
||||||||||
ловие Гаусса-Маркова теперь выполняется. |
|
|
|
|
|
|
|
|
|||
Далее можно с помощью обычного МНК вычислить параметры уравнения (48), т.е. найти |
|||||||||||
оценки: |
|
β0=b2 a3 |
|
и β1=b1 a1 |
|
|
|||||
|
|
|
|
|
|||||||
|
|
|
a2 |
|
|
|
a2 |
|
|
|
|
Однако, зная β0 и β1, мы не сможем найти значения параметров исходных уравнений системы (47), так как их слишком много. Эта проблема в эконометрике называется проблемой идентифицируемости. Об этой проблеме необходимо помнить еще на этапе формирования модели.
Если, определив значение параметров приведенной системы одновременных уравнений, невозможно однозначно определить значения параметров исходной системы, то исходная система на-
зывается неидентифицируемой.
Если же для параметров исходной системы можно найти несколько различных оценок, которые не согласуются между собой, то исходная система называется сверхидентифицируемой (или переопределенной). Ситуация переопределенности обычно возникает когда в исходную систему уравнений входит больше экзогенных переменных, чем число уравнений в системе.
Подробнее о неидентифицируемости и сверхидентифицируемости формы эконометрической модели можно узнать из [ ]. Рассмотрим пример идентифицируемой модели:
|
y |
|
|
x |
|
y |
|
|
e |
|
(49) |
|||||||||
|
|
1 |
|
1 |
|
1 |
1 |
|
|
2 |
1 |
|
|
|||||||
|
y1 2 x2 2 y1 e2 , |
|
|
|
||||||||||||||||
где x1, x2 – эндогенные; y1, y2 – экзогенные переменные. |
|
|
||||||||||||||||||
Разрешая систему (49) относительно экзогенных переменных y1 |
и y2, получаем: |
|||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 1 |
|
x2 e2 1 e1 , |
|
||
y1 |
|
|
|
|
|
|
|
|
x1 |
|
|
|
(50) |
|||||||
1- 1 2 |
1- 1 2 |
|||||||||||||||||||
|
|
|
|
1- 1 2 |
|
|||||||||||||||
|
|
|
|
1 2 |
|
|
|
|
|
|
|
2 |
|
e1 2 e2 , |
|
|||||
y2 |
|
|
|
|
|
x1 |
|
|
|
x2 |
|
|||||||||
|
1- 1 2 |
|
1- 1 2 |
|
||||||||||||||||
|
|
|
|
|
|
1- 1 2 |
|
|||||||||||||
Система (50) разрешена относительно экзогенных объясняемых y1 и y2, роль объясняющих переменных играют эндогенные переменные x1 и x2. Поэтому препятствие для применения обычного МНК (коррелированность объясняемых переменных со случайными членами) в системе (50) устранена. После применения МНК получим оценки параметров уравнений системы (50), откуда находим оценки параметров исходной системы (49).
a1 |
|
|
|
1 |
|
|
, |
|
|
|
1 a2b1 |
|
|
||||
|
|
|
|
1 |
a1 |
, |
|||||||||||
1- 1 |
|
|
|||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
a1b2 |
|
||||
|
|
|
|
2 1 |
|
|
|
|
|
|
|
|
|
|
a2b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a2 |
|
|
1- 1 |
, |
2 |
b2 |
1 |
a1b2 |
|
, |
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
||
b1 |
|
|
|
|
, |
1 a2 , |
|
|
|
||||||||
1- 1 |
|
|
|
|
|||||||||||||
|
|
2 |
|
|
|
|
|
|
b2 |
|
|
|
|
|
|||
b2 |
|
|
2 |
; |
|
|
b1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
. |
|
|
|
||||||
|
|
|
1- 1 2 |
a1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, параметры уравнений системы (49) найдены. Примененный метод, связанный с преобразованием системы уравнений (49) к приведенному виду (50), последующим применением МНК и вычислением значений исходных параметров называется косвенным методом наименьших квадратов (КМНК).
В случае сверхидентифицируемости исходной модели, состоящей из системы одновременных уравнений, применяется двухшаговый метод наименьших квадратов (ДМНК). Суть его заключается в том, что на первом шаге обычным МНК оцениваются параметры приведенной формы модели, в которой в левых частях уравнений содержатся только экзогенные объясняемые переменные. Расчетные значения этих переменных затем подставляются в уравнения исходной модели, и снова обычным МНК рассчитываются параметры уравнений исходной модели.
ДМНК применяется также при наличии в модели лаговых переменных [2, 3]. Двухшаговый метод наименьших квадратов входит в большинство современных пакетов эконометрических программ.
Для оценки параметров в случаях неидентифицируемости модели используется трехшаговый метод наименьших квадратов (ТМНК) [3]. Практическая реализация этого метода также связана с использованием пакетов эконометрических программ.
Вопросы к теме:
1.Приведите пример системы одновременных уравнений.
2.В чем причина невыполнения некоторых равенств в системе одновременных уравнений, включающих расчетные значения экзогенных переменных?
3.В каком случае система одновременных уравнений называется неидентифицируемой?
4.В чем причина неопределенности (сверхиднетифицируемости) исходной системы одновременных уравнений?
4.Приведите пример идентифицируемой исходной системы.
6.В чем суть косвенного метода наименьших квадратов(КМНК) для вычисления параметров идентифицируемой исходной системы?
7.В чем суть ДМНК?
8.В каких случаях применяется трехшаговый метод наименьших квадратов(ТМНК)?

Лекция 13. ПРЕДСКАЗАНИЯ. ПРОГНОЗЫ
13.1.Авторегрессионная модель
иARMA-модель Бокса-Дженкинса
Допустим, что исследовалась зависимость величины y(t) от величины x(t). Пусть в результате эконометрического анализа найдена следующая линейная регрессионная модель:
y(t) a0 a1x(t) ut (t=1,2,…,T). (51)
С помощью этой модели можно делать предсказания типа: если спустя время «p» значение переменной x(t) станет равным xT p , то y(t) будет иметь значение
ŷT p a0 a1xT p .
Предсказания не учитывают те изменения, которые могут произойти за период времени «p», поэтому делать предсказания оправдано лишь в том случае, когда зависимость y(t) от x(t) выполняется достаточно строго и нет оснований предполагать, что за период «p» произойдут какие-либо собы-
тия, которые могут повлиять на параметры модели a0 и a1 .
Экономисты-теоретики предпочитают делать предсказания на основании моделей типа (51). Модели могут быть нелинейными, могут содержать не одну, а несколько объясняющих переменных
x1(t); x2 (t);...;xk (t), и при их выработке используются как теоретические положения, так и эконо-
метрический анализ статистических данных.
Однако широкую публику (политиков, журналистов, обывателей) обычно мало привлекают рассуждения экономистов-теоретиков на тему: «если x1(t) примет значение « », а x2 (t) значе-
ние « », то значение переменной y(t) станет равным « ». Широкую публику более интересуют
прогнозы, т.е. предсказания типа: «через «p» лет значение переменной y(t) станет равным yT p ,
которые имеют безусловный характер, не зависящий от других факторов.
Для формулировки прогнозов относительно значений y(t) можно в качестве прогностической модели использовать не только модели типа (51), но и так называемые авторегрессионные модели
(AR-модели). Простейшая AR-модель (модель |
-го порядка) имеет вид: |
|
y(t) b0 b1 y(t 1) t |
, (t=1,2,…,T). |
(52) |
Прогнозы менее точны, чем предсказания, поскольку они подвержены дополнительному источнику ошибки – предварительному предсказанию значений объясняющей переменной xT p . (Заме-
тим, что объясняющих переменных может быть несколько).
Однако многие авторитетные экономисты считают, что в области макроэкономики проблемы мультиколлинеарности, невозможность правильной спецификации ввиду отсутствия необходимой информации и т.п. делают «обычные» модели типа (51) неэффективными. В то же время AR-модели часто дают намного более точные прогнозы, чем предсказания на основе моделей типа (51).
Боксом и Дженкинсом разработан метод, который основан на использовании
AR-модели порядка «p» в сочетании с методом скользящей средней (MAмодель от англий-
ского «movning average»).
ARMA-модель Бокса-Дженкинса порядка p, q имеет вид:
yt b0 b1yt 1 ... bp yt p 0 t t 1 ... q t q , |
(53) |
где yt 1,yt 2,...,yt p - значение переменной y(t) в предыдущие моменты времени; |
t, t 1,..., t q - независи- |
мо распределенные случайные члены с нулевым средним значением.
В последние годы больше внимания стали уделять так называемым «простым» или «наивным» прогнозам. Например, изменение исследуемой переменной y(t) (приращение y(t)) в буду-
щем году можно оценить как среднее значение приращений i y(t) за последние «n» лет
(i=1,2,…,n). То есть:
y(t)= 1 y(t) ... n y(t) . n
«Простые» методы прогнозирования довольно часто работают лучше, чем «теоретические» макроэкономические модели. В 1972 году Р.Купер сравнил функционирование шести различных макроэкономических моделей развития экономики США и обнаружил, что получаемые с их помощью прогнозы уступают по точности прогнозам, составленным на основе авторегрессионной модели.

13.2. Доверительный интервал для предсказаний (прогнозов) значений объясняемой переменной
Если для предсказания (прогнозирования) значения переменой у используется какое-либо уравнение регрессии, то возникает вопрос о том, на какую глубину (на какой срок) можно делать предсказания и как оценивать достоверность этих предсказаний.
Можно обосновать статистически, что период, на который можно делать достаточно точные прогнозы, должен быть по меньшей мере в три раза короче, чем период, для которого было найдено уравнение регрессии [1]. Для приближенной оценки пригодности уравнения регрессии для предска-
зания (прогнозирования) значения y0,пр. используют отношение:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
S |
1 |
|
|
|
|
|
|
ui2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
S - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
y |
|
y |
|
|
|
n m |
|
|
|
|
|
|
|
|
|
|
y ; m - |
|||||||||
где |
стандартная |
ошибка |
|
уравнения |
регрессии; |
|
|
|
|
|
- выборочное среднее |
переменной |
|||||||||||||||||||||||||||||||||||||||||
|
количество параметров в уравнении регрессии. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
Величина V |
позволяет приближенно оценить среднюю относительную ошибку прогнозиро- |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
вания величины y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Для нахождения «точной» интервальной оценки значений y0,пр. |
при x x0 (в случае парной |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
линейной регрессии) необходимо вначале найти величину Sy0,пр. : |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Sy |
|
. S |
1 |
1 |
|
|
|
x0 |
|
x |
2 |
|
, |
|
|
|
|
|
|
(54) |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0,пр |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
где S |
Ui2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
i 1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Если число объясняющих переменных в уравнении регрессии равно P (P 1), то: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sy |
. S |
|
1 |
|
|
0T (XT X) 1 |
|
0 , |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
X |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,пр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
Ui2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где |
i 1 |
|
|
; Х – |
матрица значений объясняющих переменных (см. лекцию 5); |
|
0 - вектор их |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
X |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
n p 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
предполагаемых значений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Доверительный интервал для предсказываемого (прогнозируемого) значения y0,пр. |
в любом |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
случае имеет вид: |
|
|
€ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
€ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 ;n p 1 |
|
|
|
|
|
|
|
|
|
|
t1 ;n p 1 |
|
Sy0,пр . |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
0 |
|
|
|
Sy0,пр . ; y0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
где t1 ;n p 1 - значение t |
- статистики Стъюдента, определяемое по таблице. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
нии: |
Задача. Имеются данные относительно динамики изменения курса акций некоторой компа- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
t |
1 |
|
2 |
|
|
|
3 |
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
7 |
|
8 |
|
|
|
9 |
10 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
yt |
16,3 |
|
20,2 |
|
17,1 |
|
17,7 |
|
|
15,3 |
|
|
|
|
16,3 |
|
19,9 |
|
14,4 |
|
18,7 |
20,7 |
|
|
|
|
|||||||||||||||||
1.Используя AR-модель -го порядка, составить уравнение модели и сделать прогноз на глубину p=2, т.е. t=12.
2.Найти доверительный интервал этого прогноза при 0,05.
Решение.
1. y(t) b0 b1 y(t 1) t , где согласно МНК (методу наименьших квадратов)

|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
||||
|
|
|
b0n b1 |
t yt , |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
t 1 |
|
t 1 |
|
|
|||||
|
|
|
|
|
n |
|
|
|
n |
|
|
n |
(55) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
ytt. |
|
|
|||
|
|
|
b0 t b1 t |
|
|
|
|||||||||||||
|
|
|
|
t 1 |
|
|
|
t 1 |
|
|
t 1 |
|
|
||||||
|
n |
n(n 1) |
|
|
|
|
|
n |
|
|
n(n 1)(2n 1) |
|
|
|
|||||
При этом: t |
; |
|
|
t2 |
|
. |
|
|
|||||||||||
|
|
|
|
|
|
6 |
|
|
|||||||||||
|
t 1 |
2 |
|
|
|
|
|
|
|
t 1 |
|
|
|
|
|
||||
|
|
|
10 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
||
Так как n=10, то: t 55; |
t2 |
385. |
|
|
|||||||||||||||
|
|
|
t 1 |
|
|
|
|
|
|
|
t 1 |
|
|
|
|
|
|
||
|
10 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
Кроме того yt 176,6; |
|
ytt 982,9. |
|
|
|||||||||||||||
|
|
t 1 |
|
|
|
|
|
|
|
|
|
|
t 1 |
|
|
|
|
|
|
Таким образом, система (53) принимает вид: |
|
|
|||||||||||||||||
|
|
|
|
|
10b |
55b 176,6, |
b 16,89, |
||||||||||||
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
0 |
|||||
|
|
|
|
|
55b0 |
385b1 |
982,9. |
b1 0,14. |
|||||||||||
|
|
|
y(t)=16,89+0,14∙y(t-1) . |
(56) |
|||||||||||||||
Зная y(10)=20,7 найдем с помощью модели (56): |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y(11)=16,89+0,14∙20,7=19,79 |
|||||||
Зная y(11)=19,7, найдем с помощью той же модели (56) y(12): |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y(12)=16,89+0,14∙19,79=19,66. |
|||||||||
2. Найдем с помощью уравнения (56) расчетные значения y€(t). Причем y€(1) будем считать |
|||||||||||||||||||
равным y€(1) 16,3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n |
|
|
10 |
|
y€i 2 |
|
|
|
|
|
|
|
|||||||
Найдем Ui2 |
yi |
|
64,5. |
|
|
||||||||||||||
i 1 |
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ui2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда S |
|
64,5 |
|
|
|
|
|
|
|
|
|||||||||
|
i 1 |
|
|
|
|
|
|
|
|
|
2,84. |
|
|
|
|
||||
|
|
|
8 |
|
|
|
|
|
|
||||||||||
|
|
n 2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
||
Кроме того, найдем t0 |
|
|
|
|
2 |
12 5,5 2 42,25, и (t |
ti )2 82,5. |
||||||||||||
|
t |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
||
Тогда по формуле (54) Sy |
|
: |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
0,пр. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Sy |
|
3,6; по таблице t0,95;8 |
2,31. |
||||||||
|
|
|
|
|
|
|
|
|
|
0,пр. |
|
|
|
|
|
|
|||
Доверительный интервал прогнозируемого значения y(12) будет: |
|||||||||||||||||||
|
|
|
|
|
|
|
(19,66 3,6 2,31; 19,66 3,6 2,31) |
||||||||||||
|
|
|
|
|
(19,66 8,3; |
19,66 8,3) (11,36;27,93), |
|||||||||||||
то есть y(12) с вероятностью 0,95 будет принадлежать интервалу (11,36;27,93).
Вопросы к теме:
1.Приведите пример модели, пригодной для того, чтобы делать предсказания.
2.В чем разница между предсказанием и прогнозом.
3.Какие модели используются для формулирования прогнозов?
4.Приведите пример модели «наивного» (простого) прогноза.
5.Сформулируйте ARMA-модель Бокса-Дженкинса по двум предыдущим значениям.
