
The Physics of Coronory Blood Flow - M. Zamir
.pdf2.10 Summary |
77 |
correspondence between the two is fairly clear. A great advantage of the electrical analogy is the availability of well developed mathematical analysis of electric circuits of a wide range of complexity which would be fairly di cult to formulate in terms of either the fluid flow or the mechanical system.

3
Basic Lumped Elements
3.1 Introduction
A lumped model of the coronary circulation must at a minimum include the three basic elements of resistance, inductance, and capacitance, which we shall associate with their respective constants R, L, C, as was done in previous sections, and refer to the combination of the three elements generically as the “RLC system”. The reason for this minimum requirement is that the coronary circulation, being a fluid flow system, involves the movement of a fluid that has mass and is therefore associated with inductance when accelerated or decelerated; the moving fluid is viscous and is therefore subject to resistance resulting from the no-slip boundary condition at vessel walls; and the vessels are elastic, thus allowing changes in volume that produce capacitance e ects.
What is not known, of course, is whether these elements can indeed be considered as “lumped” in the dynamics of coronary blood flow. Thus, any lumped model analysis must begin with the assumption that this can be done. That is, it must be assumed that the inductance e ects of blood flow in the labyrinth of vessels in the coronary circulation can be represented by a single inductance parameter L; that the viscous e ects at the walls of the same labyrinth of vessels can be represented by a single resistance parameter R; and that the elasticity e ects of all of these vessels can be represented by a single capacitance parameter C. There are no clear grounds for making these assumptions, nor any direct ways of assessing their validity, because of the severe di culties involved in any attempt to measure these parameters directly from the coronary circulation. A more hopeful prospect of assessing the validity of “lumped” parameters is that of comparing the dynamics of an assumed lumped model with any measurable dynamics of the coronary circulation and thus assessing indirectly the validity of the model and of the lumped parameters on which it is based. Indeed, the validity of using the LRC model rests on this prospect rather than on the legitimacy of the lumped model concept.
80 3 Basic Lumped Elements
In using the RLC system it must also be assumed that the dynamics of the coronary circulation are governed by only these three parameters. This assumption, again, cannot be supported on any direct grounds, in fact it can be disputed on the indirect ground that there are observed e ects in the coronary circulation which cannot be readily represented by the three basic elements. One such e ect which has so far proved very di cult to model is the so-called “tissue pressure e ect” or the e ect of “cardiac muscle contraction”. This e ect arises because much of the coronary vasculature is actually imbedded within the myocardium, and when the muscle contracts as it does within each cardiac cycle, it exerts considerable pressure on the coronary vessels to the extent of slowing down or even reversing the flow in some vessels, or possibly collapsing the vessels momentarily within each cardiac cycle [84, 20, 68, 187, 41, 101]. Not only are the details of this scenario poorly known, but its modelling has been particularly troublesome [96, 97].
A similar e ect in this category is that of wave reflections. Wave reflections are ubiquitous in the coronary circulation because of the pulsatile nature of the flow and because of the large number of vascular junctions where reflections occur [219, 221]. The e ect of these on coronary blood flow, or more accurately the way in which these e ects are integrated into the design and dynamics of the coronary circulation, is not known.
A related issue is that of the distinctness of R, L, C elements within the coronary blood flow system. While it can be argued that resistance, inductance, and capacitance e ects must exist in the coronary circulation, that is not to say that they must exist in “pure” form, distinct from each other as they do in an electric circuit. Changes in vessel diameters associated with capacitance e ects, for example, clearly have an e ect on the resistance to flow because it depends critically on the diameter of the vessel. Thus, the capacitance and resistance e ects are not entirely independent from each other, they do not exist in a pure or distinct form.
Furthermore, coronary vessels are not only elastic but muscularized, thus changes in vessel diameters may occur not only passively with pressure changes but also actively in the course of regulation of coronary blood flow [83, 128]. While such active changes in diameters a ect both the resistance to flow and capacitance of the system, these e ects cannot usually be included in a primary lumped model of the coronary circulation because they result from neural or humoral regulatory mechanisms that originate outside the primary fluid dynamic system.
It may seem odd to proceed with the RLC system in the face of such major unknowns, but the grounds for proceeding are twofold. First, as argued earlier, these elements must exist within the physiological system in some form, even if not lumped or distinct. Thus, the RLC system, even if not ultimately accurate, provides a reasonable approximation with which to start. Second, the nature of the physiological setting, namely that of a beating heart and deeply imbedded vasculature, is such that the location and arrangement of these elements cannot be determined directly from the physiological sys-
3.2 RLC System in Series |
81 |
tem. The lumped model concept is based on the prospect that they can be determined indirectly, by modelling.
3.2 RLC System in Series
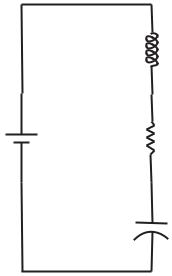
When the elements of resistance R, inductance L, and capacitance C are in series, their e ects simply add up against the force driving the flow. Thus, in the electrical system shown in Fig. 3.2.1, the equation governing the flow of current I under the driving voltage V , using the results and notation of Section 2.9, is given by
L |
dI |
+ RI + |
|
1 |
|
Idt = V |
(3.2.1) |
dt |
C |
||||||
L
V R
C
Fig. 3.2.1. The electrical RLC system in series. Flow of electric charge (current) is driven by the voltage V and opposed by an inductor (L), resistor (R), and capacitor (C), in series.
Similarly, in the mechanical analogy shown in Fig. 3.2.2, the equation governing the velocity u of the moving mass under the driving force F , using the results and notation of Section 2.8, is given by
du |
+ Ru + |
1 |
|
udt = F |
(3.2.2) |
||
L |
|
|
|
||||
dt |
C |
||||||
While in this case the inductance L is equal to the mass m of the moving object (Eq. 2.8.2), the resistance R is equal to the friction coe cient f (Eq. 2.8.4),
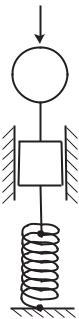
82 3 Basic Lumped Elements
F
mL
R
C
Fig. 3.2.2. The mechanical RLC system in series. Motion (velocity) of mass m is driven by a force F and opposed by the inertia of the mass, thus giving rise to inductance (L), by the friction force of a damper, thus giving rise to resistance (R), and by the force of a spring, thus giving rise to capacitance (C).
and the capacitance C is equal to the reciprocal of the spring constant k (Eqs.2.8.6,8), we continue to use the symbols R, L, C in a generic manner in order to highlight the analogy between the electrical and mechanical systems, and in order to make the discussion and analysis of the governing equation the same for both systems.
Finally, in the fluid flow system shown in Fig. 3.2.3, the equation governing the flow rate q produced by the driving pressure di erence Δp, using the results and notation of Sections 2.4,5,6, is given by
L |
dq |
+ Rq + |
1 |
|
qdt = Δp |
(3.2.3) |
dt |
C |
Again, while the inductance L and resistance R for flow in a tube can be expressed in terms of properties of the fluid and of the tube (Eqs.2.4.5,2.5.5), and for flow into an elastic balloon the capacitance C can be expressed in terms of changes in the volume of the balloon (Eq. 2.6.4), we continue to use the generic symbols R, L, C instead, as discussed earlier.
It is clear that in the fluid flow case of Fig. 3.2.3 the arrangement of the three elements in series is not appropriate as a model of the physiological
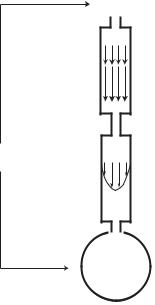
3.2 RLC System in Series |
83 |
p2
L
p = p2 - p1
R
p1 C
Fig. 3.2.3. The fluid dynamic RLC system in series. Fluid flow is driven by a pressure di erence Δp = p2 − p1 and opposed by the inertia of the fluid, thus giving rise to inductance (L), by the viscous resistance at the tube wall, thus giving rise to resistance (R), and by the elasticity of a balloon, thus giving rise to capacitance (C). Because of the series arrangement, flow is forced to go into or out of the balloon and is therefore limited by its capacity. There is no outflow from the system, and continuous flow is clearly not possible.
system because the flow is forced into or out of the balloon and is therefore limited by the capacity of the balloon. There is no outflow from the system. While it is possible to modify the model as in Fig. 3.2.4 to produce an outflow, flow through the system, whether inflow or outflow, is still limited by the capacity of the balloon. Continuous flow is not possible. Thus, the RLC system in series is not a good model of the physiological system where continuous flow is an essential feature. Nevertheless, for analytical and pedagogical reasons, this model provides an important starting point and a useful reference.
For the analysis to follow, we use the fluid flow analogue of the RLC system governed by Eq. 3.2.3. It is convenient to reduce the number of physical parameters involved in this equation, so that the solution of the equation does not require the actual values of R, L, C. We do this by dividing the equation by the resistance R to give
dq |
1 |
|
qdt = |
Δp |
|
||
tL |
|
+ q + |
|
|
(3.2.4) |
||
dt |
tC |
R |
|||||
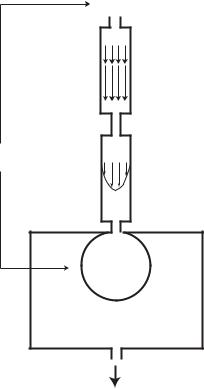
84 3 Basic Lumped Elements
p2
L
p = p2 - p1
R
p1 C
Fig. 3.2.4. Fluid dynamic RLC system in series, as in Fig. 3.2.3, but modified to allow flow out of the system. The balloon is enclosed within a rigid box filled with the same fluid, thus expansion of the balloon forces fluid out of the box as shown by the arrow. Flow is still limited by the capacity of the balloon, however, and continuous flow is not possible.
where tL (= L/R) and tC (= RC) are respectively the inertial and capacitive time constants introduced in Sections 2.5,6, which are measures of the inertial and capacitance e ects as described in those sections.
Finally, as we found previously, it is more convenient to di erentiate this equation once to eliminate the integral term in the equation, giving
|
d2q |
|
dq |
1 |
|
1 d(Δp) |
|
|||
tL |
|
+ |
|
+ |
|
q = |
|
|
|
(3.2.5) |
dt2 |
dt |
tC |
R dt |
|||||||
3.3 Free Dynamics of the RLC System in Series
In this section we examine the dynamics of the RLC system in the absence of any external force driving the system and refer to this as a state of “free

3.3 Free Dynamics of the RLC System in Series |
85 |
dynamics”. In the governing equation (Eq. 3.2.5) this means that Δp ≡ 0, thus the term on the right side of the equation is zero and the equation reduces to
|
d2q |
+ |
dq |
1 |
q = 0 |
(3.3.1) |
||
tL |
|
|
|
+ |
|
|||
dt2 |
|
dt |
tC |
|||||
It is seen from this form of the equation that the inertial and capacitive time constants tL, tC play a critical role in the free dynamics of the RLC system, since they are the only parameters present in the equation, thus their values critically a ect the solution of this equation. This is particularly meaningful because the values of tL, tC actually represent measures of the inertial and capacitance e ects in the system as discussed in previous sections. Thus, these time parameters now allow a study of the free dynamics of the system without the need to specify the values of the physical parameters R, L, C individually.
Equation 3.3.1 is a standard second order linear di erential equation with constant coe cients [116]. Its solution depends on the nature of the roots of the associated (so called “indicial”) equation
tLα2 + α + |
1 |
= 0 |
(3.3.2) |
||
|
|||||
|
|
tC |
|
||
The roots are in general given by |
|
|
|
|
|
|
|
|
|
||
2tL |
|
||||
α = |
−1 ± |
1 − (4tL/tC ) |
(3.3.3) |
||
|
|
||||
but the solution of the governing equation (Eq. 3.3.1) and hence the dynamics of the system depend critically on whether these roots are real or complex, which in turn depends on the relative values of the time constants tL, tC .
If 4tL < tC , then Eq. 3.3.2 has two distinct real roots, given by
|
1 |
|
− |
|
|
2tL |
|
α |
|
= |
|
1 + |
1 |
− (4tL/tC ) |
|
2 |
− |
1 |
− |
|
|
||
|
|
|
|||||
|
|
2tL |
|||||
α |
|
= |
|
|
|
|
− (4tL/tC ) |
|
|
|
|
|
|
||
and the solution of the governing equation is given by
q(t) = Aeα1t + Beα2t
(3.3.4)
(3.3.5)
(3.3.6)
where A, B are arbitrary constants. Given the values of the flow rate at time t = 0, namely q(0), and the rate of change of the flow rate at the same time, namely q (0), we find
A = |
−α2q(0) + q (0) |
(3.3.7) |
|
α1 − α2 |
|||
|
|
||
B = |
α1q(0) − q (0) |
(3.3.8) |
|
α1 − α2 |
|||
|
|

86 3 Basic Lumped Elements
If 4tL > tC , then Eq. 3.3.2 has two complex (conjugate) roots, given by
|
α1 = a + ib |
|
|
|
(3.3.9) |
|||||
|
α2 = a − ib |
|
|
|
(3.3.10) |
|||||
where |
|
|
|
|
|
|
|
|
|
|
a = |
|
−1 |
|
|
|
|
|
(3.3.11) |
||
|
2tL |
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
b = |
|
|
|
|
2tL |
− |
1 |
|
(3.3.12) |
|
|
|
|
(4tL/tC ) |
|
|
|
||||
i = |
√ |
|
|
|
|
|
|
(3.3.13) |
||
|
|
−1 |
|
|
|
|
|
|||
and the solution of the governing equation is given by |
|
|||||||||
q(t) = eat{A cos(bt) + B sin(bt)} |
(3.3.14) |
|||||||||
where A, B are arbitrary constants. Given the values of q(0) and q (0), again, we find
A = q(0)
B = −aq(0) + q (0) (3.3.15) b
If 4tL = tC , then Eq. 3.3.2 has two identical real roots, given by
α1 = α2 = a = |
−1 |
(3.3.16) |
|
2tL |
|||
|
|
and the solution of the governing equation is given by
q(t) = (A + Bt)eat |
(3.3.17) |
where A, B are arbitrary constants. Given the values of q(0) and q (0), we find
A = q(0) |
|
||
B = |
− |
aq(0) + q (0) |
(3.3.18) |
|
|||
Examples of these three scenarios are shown in Fig. 3.3.1. It must be remembered that the flow under these scenarios is free from any external driving force, but it is subject to the e ects of inertia (L), resistance (R), and capacitance (C). The dynamics of the system are “free” in the sense that the system is under only these internal forces.
Unlike the situation discussed in Section 2.6 where the capacitor is in parallel with a resistor and hence flow has the option of going into the balloon or into the tube, in the present scenario the capacitor is in series and hence flow has no option but to go into the balloon. Clearly, this situation is ultimately
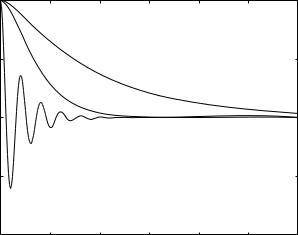
flow rate q (normalized)
3.3 Free Dynamics of the RLC System in Series |
87 |
1
0.5
0
−0.5
−10 |
5 |
10 |
15 |
20 |
25 |
30 |
|
|
|
t / tL |
|
|
|
Fig. 3.3.1. Free dynamics of the RLC system in series with 4tL/tC = 0.4 (top curve), 4tL/tC = 1 (middle curve), and 4tL/tC = 40 (bottom curve). The top and bottom curves illustrate two di erent types of dynamics usually referred to as “overdamped” and “underdamped” respectively. The middle curve represents the singular dynamics, usually referred to as “critically damped”, which lies between the two types of behaviour.
limited by the maximum size to which the balloon can stretch, but we ignore this limit for the present and assume that the dynamics of the system are taking place before the limit is reached.
At time t = 0 the dynamics are triggered with a pre-existing flow rate q(0) through the system, and for the purpose of illustration we take q(0) = 1 and q (0) = 0. This flow will diminish because it has no external driving force and it is opposed by the tube resistance R and by the elasticity of the balloon wall as flow stretches it. The only driving force which keeps some flow going at this phase is an internal force due to the inertial e ect, namely the momentum which the fluid has by virtue of the pre-existing velocity with which it was started. Since this momentum is finite and is not being renewed by any external force, it is ultimately exhausted and the fluid comes to rest. The flow rate becomes zero.
At this point one of two possible scenarios may unfold: the balloon may recoil and send fluid back, thus reversing the flow direction, or the balloon may simply absorb the increased volume of fluid and come to equilibrium at a new volume. In the mechanical system analogy this is equivalent to the compression (or expansion) of a spring, which may take place either “gently” so that the spring may simply reach equilibrium at a new length, or it may
