
физика лабы 1 курс
.pdfЛабораторная работа №9 Определение коэффициента поверхностного натяжения жидкости
Приборы и принадлежности: установка, набор испытуемых жидкостей, бюретки, стаканчики, сосуд, микрометр, штангенциркуль.
Введение В жидкостях среднее расстояние между молекулами много меньше, чем в газах, и силы
взаимодействия играют существенную роль. Поверхность жидкости, соприкасающаяся с другой средой (собственным паром, другой жидкостью, твердым телом), находится по сравнению с остальной массой жидкости в равновесии. Каждая молекула внутри жидкости испытывает одинаковое взаимодействие во всех направлениях. Молекулы же, расположенные вблизи поверхности, взаимодействуют с молекулами граничащей среды, при этом силы, действующие на каждую молекулу поверхностного слоя, оказываются неуравновешенными. Равнодействующая сила направлена внутрь жидкости, если она граничит с собственным паром. Молекулы поверхностного слоя имеют кинетическую энергию теплового движения и потенциальную, обусловленную силами межмолекулярного взаимодействия. Кинетическая энергия молекул поверхностного слоя и внутри жидкости одинакова (для случая, если температура одинакова во всем объеме). Иначе обстоит дело с потенциальной энергией. При переходе молекул из внутренней части жидкости на ее поверхность, они совершали работу против направленных внутрь жидкости сил притяжения со стороны других частиц жидкости. Эта работа идет на увеличение потенциальной энергии молекул, переходящих в поверхностный слой. Поэтому частицы этого слоя обладают большей потенциальной энергией, чем частицы жидкости. В состоянии равновесия система стремиться занять положение с минимальной энергией, т.е. жидкость в состоянии равновесия будет иметь минимальную возможную поверхность. Это означает, что должны существовать силы, препятствующие увеличению поверхности. Эти силы и называются силами поверхностною натяжения, а направлены они по касательной к поверхности. Для увеличения поверхности необходимо совершать работу, которая затрачивается на выход молекул из глубины на поверхность
dA dS |
( 1 ) |
Знак (-) указывает, что увеличение поверхности сопровождается отрицательной работой. При |
|
сокращении поверхности совершается положительная работа. Коэффициент |
– основная |
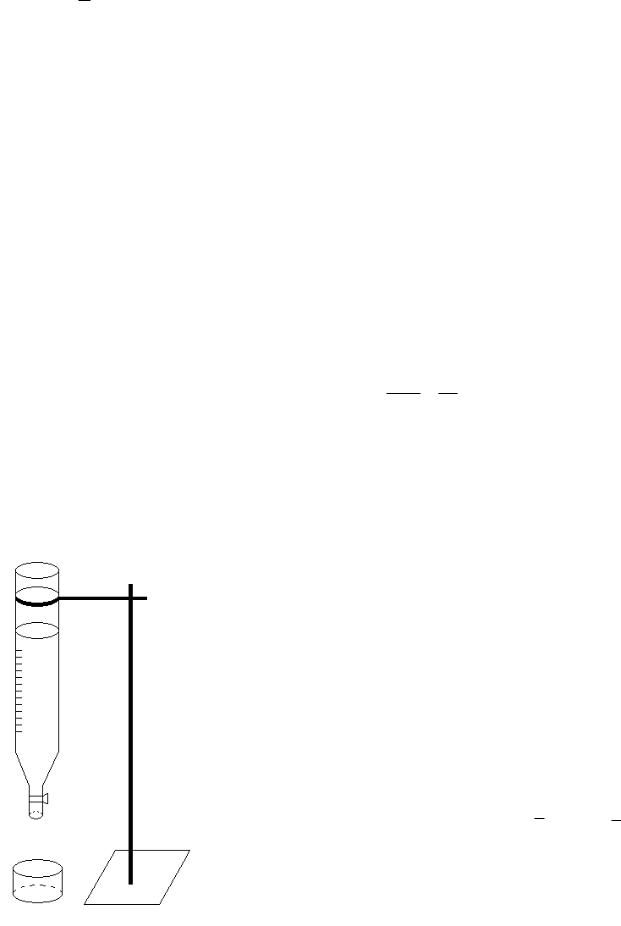
величина, характеризующая свойства поверхности жидкости, А – работа, необходимая для увеличения поверхности жидкости при постоянной температуре на единицу площади. В системе Си [α]= Дж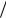 м2 . Коэффициент поверхностного натяжения может быть определен и как величина, равная силе, действующей по касательной к поверхности, приходящей на единицу длины линии разрыва.
м2 . Коэффициент поверхностного натяжения может быть определен и как величина, равная силе, действующей по касательной к поверхности, приходящей на единицу длины линии разрыва.
В системе СИ [α]= Н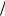 м . Коэффициент поверхностного натяжения должен быть определен разными способами.
м . Коэффициент поверхностного натяжения должен быть определен разными способами.
Малый объем жидкости, благодаря малой массе (силе тяжести), за счет действия силы поверхностного натяжения принимает шарообразную форму. Это явление лежит в основе метода капель - одного из способов определения коэффициента поверхностного натяжения.
Если благодаря соприкосновению с твердым телом, поверхность жидкости получит некоторую кривизну, то на такой поверхности силы натяжения вызывают некоторые дополнительные явления. Эти силы дают при выпуклых и вогнутых поверхностях слагающую всегда в сторону вогнутой поверхности, и таким образом, создают внутри всякой искривленной поверхности добавочное давление
|
2 |
( 2 ) |
|
R |
|||
|
|
R - радиус кривизны поверхности. Этим добавочным давлением, т.е. давлением, обусловленным кривизной R, вызываются явления поднятия и опускания жидкости в капиллярных трубах. Жидкость поднимается и (опускается) в капилляре настолько, чтобы гидростатическое давление столба жидкости уравновесило давление, вызванное кривизной поверхности. Если считать, что жидкость полностью смачивает поверхность трубки, то R - совпадает с внутренним радиусом трубки r , так что
|
2 |
gh |
( 3 ) |
|
|||
|
r |
|
|
- плотность жидкости; h - высота ее подъема;r - радиус капилляра.
Таким образом, зная ρ, h, r можно определить коэффициент поверхностного натяжения.
Упражнение 1 Метод капель
Опыт заключается в определении той силы, под действием которой отрывается капля. Зная эту силу, которая удерживает каплю до падения, легко определить α:
P S
При вытекании капель жидкости из трубки размер капли нарастает постепенно, но отрывается только тогда, когда вес капли станет равным силе поверхностного натяжения, удерживающей ее, т.е.
2 r |
( 4 ) |
|||
|
|
( 5 ) |
||
|
|
|||
2 r |
||||
|
|
|||
Р – вес капли;r – радиус шейки капли.
Однако ввиду того, что радиус шейки отрывающейся капли определить трудно, абсолютные измерения поверхностного натяжения этим методов будут недостаточно точны. Если ограничиться относительными измерениями, та можно обойтись без измерения радиуса шейки капли. Допустим, что некоторый определенный объем содержит n1 капель одной жидкости и n2 капель другой, тогда обозначив через 1 и 2 , плотности жидкостей, можно написать:
Вес одной капли 1-ой жидкости
Вес n1 |
1 2 r 1 |
|
|
( 6 ) |
капель 1-ой жидкости |
|
|
|
|
|
n1 1 2 r 1n1 1V |
|
( 7 ) |
|
Вес одной капли 2-ой жидкости 2 2 r 2 |
|
|
|
|
Вес |
n2 капель 2-ой жидкости n2 2 2 r 2n2 |
2V . Здесь |
n1 1 и |
n2 2 веса первой и второй |
жидкости и объеме V. Взяв отношение (6) и (7), имеем: n1 1 1 ,
Откуда можно определить |
|
|
n2 2 |
2 |
|
|
n1 2 |
|
|
||
2 |
|
1 |
( 8 ) |
||
|
|||||
|
|
n2 1 |
|
||
Обычно в качестве жидкости с известным коэффициентом поверхностного натяжения употребляется вода. Коэффициент поверхностного натяжения зависит от температуры – при повышении температуры уменьшается. Например, для воды при 20°С α1 равно 72,5 дн/см, а при 30◦ С α1 равно 71,63 дн/см
Выполнение работы
Прибор для выполнения работы очень прост. Он состоит из бюретки с краном, на которой нанесены деления (рис. 1).
Выбирают некоторый объем жидкости, например, объем жидкости, заключенной между 10-м и 12-м делениями бюретки и подсчитывают число капель каждой жидкости в этом объеме. Чтобы не смешивать жидкость, пользуются несколькими бюретками.
Повторяют опыт 5-6 раз для каждой жидкости и взяв среднюю величину, находят n1 и n2. Из таблиц «Справочника по физике» берут величины α1, ρ1, ρ2, затем вычисляют искомый коэффициент поверхностного натяжения при температуре опыта T.
Результаты опытов заносят в таблицы: Таблица 1
|
Эталонная |
и |
№ |
|
|
|
|
|
|
|
i 2 |
|
|
исследуемая |
|
|
n1 |
n2 |
α2 |
|
2 |
i |
2 |
||
|
жидкость |
|
|
|
|
|
|
|
|
|
|
|
|
Вода и спирт |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
Рис. 1 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
α1=72.5 дн/см |
|
|
|
|
|
|
|
|
|
|
|

В данном примере необходимо оценить случайную ошибку:
|
|
t |
|
( 2i |
)2 |
2 |
n, |
|
( 9 ) |
||
|
|
n(n 1) |
|||
Окончательный результат записывается как: , гдевычисляется по формуле (9).
- среднее по формуле (8)
Упражнение 2. Метод отрывания кольца
Прибор для определения коэффициента поверхностного натяжения указанным способом состоит из специальной стойки А, к которой приделана вертикальная шкала Ш, разделенная на миллиметры
(рис.).
Рис. 2. Метод отрыва кольца Перед шкалой параллельно ей подвешено на проволоке кольцо К. Кроме того к стойке в нижней
части приделан маленький столик П, могущий свободно перемещаться вверх и вниз. На этот столик ставится сосуд В с испытуемой жидкостью. В качестве сосуда может служить обыкновенный кристаллизатор (диаметр 8-10 сантиметров). Немного выше плоскости кольца к проволочке прикреплена небольшая чашечка D для грузов и небольшой указатель, который может перемещаться вдоль шкалы. Погрузим проволочное кольцо определенною диаметра, подвешенное на спиральной проволочке, в испытываемую жидкость, будет иметь место взаимодействие молекул жидкости и кольца. Плоскость должна быть строго горизонтальна.
Чтобы оторвать кольцо от жидкости, необходимо приложить определенную силу, которая нужна на разрыв поверхности пленки, имеющей соприкосновение с внешней и внутренней границей кольца. Общая длина границы пленки будет равна L d1 d2 , где d1, d2 - внутренний и внешний диаметр кольца.
Если коэффициент поверхностного натяжения обозначить через α, то сила, которая удержит кольцо в жидкости, определяется из равенства L d1 d2 . Пусть приложенная сила, при которой происходит отрыв кольца от жидкости, равна «Р». Тогда коэффициент поверхностного натяжения определяется так:
P d1 d2 |
( 10 ) |
|||
откуда |
P |
|
|
|
|
( 11 ) |
|||
d1 d2 |
||||
|
|
|||
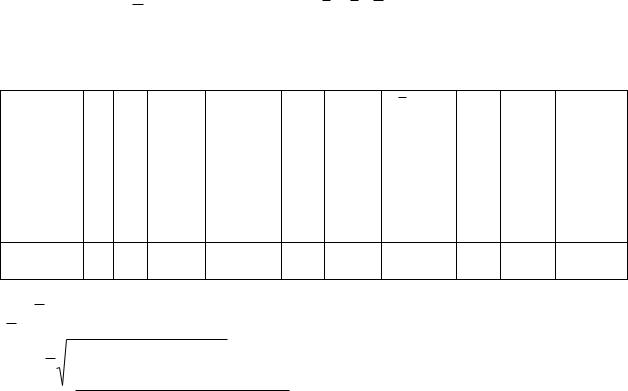
Чтобы не измерять внутренний диаметр кольца d, его величину можно исключить из формулы, т.е. d1 d2 2h, h – толщина кольца. Подставив значение в формулу, получим
|
P |
|
|
( 12 ) |
|
2 d2 |
h |
||||
|
|
||||
Выполнение работы
Устанавливают прибор таким образом, чтобы плоскость кольца строго была горизонтальна. Горизонтальность плоскости кольца проверяется прикосновением его поверхности к жидкости, затем подводят сосуд с испытуемой жидкостью под кольцо, пока оно не погрузится в жидкость. Теперь начинают медленно опускать столик П не котором находится сосуд с жидкостью. Благодаря силе сцепления кольцо тоже будет спускаться, а спираль, на которой оно подвешено, растягивается. Во время опускания внимательно следят за положением указателя.
В момент отрыва кольца от жидкости замечают положение указателя на шкале «Ш».
Чтобы определить эту силу, необходимую для отрыва кольца от жидкости, на чашечку кладут столько граммов, чтобы проволочка растянулась до такого положения, при котором произошел отрыв от жидкости. Пусть вес груза Р. При помощи штангенциркуля и микрометра измеряют внешний диаметр кольца и его толщину. Полученные значения подставляют в формулу (12)
Среднее значение вычисляется по средним d и h , P .
Опыт проделывают с одной жидкостью не менее 5-6 раз. Затем то же самое проделывают с другими жидкостями, предварительно промыв кольцо. Результаты опыта заносят в следующую таблицу:(Для каждой жидкости составить соответствующую таблицу).
Испыт. |
№ P,г |
P |
Pi |
|
|
P 2 |
d,см |
d |
di |
d |
d |
|
2 h,см |
h |
hi |
|
|
h 2 |
P |
i |
h |
||||||||||||||||
Жидкость |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Среднее
значение
Окончательный результат записывается :
, где вычисляется по формуле (I2),
|
|
P |
|
d2 |
|
h2 |
|
|
|
|
|||
|
P2 |
d h 2 |
d h 2 |
|||
|
|
|
|

 2P P2 2d d2 2h h2
2P P2 2d d2 2h h2
Контрольные вопросы:
1.Каков характер теплового движения молекул в жидкости?
2.Что такое ближний порядок?
3.В чем причина малой сжимаемости жидкости и особых свойств ее поверхностного слоя? 4.Каково условие смачивания, несмачивания жидкостью твердого тела
5.Что такое краевой угол?
6.Чем объясняется поднятие (опускание) жидкости в капиллярах?
7.Капиллярные явления в природе и технике?
8.На что затрачивается работа при увеличении поверхности жидкости?
9.Почемуприотсутствиивнешнихсилкапляжидкостипринимаетформу шара?
10.Какую работу может выполнить поверхностная пленка, сокращаясь на один см, на два см? 11.Каково практическое значение явлений поверхностного натяжения?
ЛИТЕРАТУРА
1.Грабовский Р.И. Курс физики, 1974, § 51,60,61; 1980 г. изд. 53, 61, 62,
2.Фриш С.Э., Тиморева А.В. Курс общей физики, т.1. 1963 г., §78-80, 8:..82.

Лабораторная работа №12 Изучение собственных колебаний сосредоточенной системы
Цель работы: ознакомление с закономерностями движения пружинного маятника в воздушной среде и воде.
Приборы и принадлежности: набор пружин и грузов, масштабная линейка, секундомер, сосуд с вязкой жидкостью (вода).
Введение Колебаниями называются процессы, отличающиеся той или иной степенью
повторяемости. Таким свойством повторяемости обладают, например, качания маятника часов, колебания струны или ножек камертона, напряжение между обкладками конденсатора струны или ножек камертона, напряжение между обкладками конденсатора в контуре радиопередатчика или приемника.
Простейшими являются гармонические колебания.
Гармоническими называются колебания, при которых колеблющаяся величина (например, отклонение маятника от положения равновесия) изменяется по закону синуса или косинуса.
Изучение гармонических колебаний важно по следующим причинам: во-первых, колебания в природе и в технике часто имеют характер, очень близкий к гармоническим, и вовторых, колебательные процессы иной формы могут быть представлены как наложение нескольких гармонических колебаний.
В зависимости от характера воздействия на колеблющуюся систему различают свободные (или собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания.
Свободными или собственными называют такие колебания, которые происходят в системе, предоставленной самой себе после того, как ей был сообщен толчок, либо она выведена из положения равновесия. Примером могут служить колебания шарика, подвешенного на нить (рис.1). Для того, чтобы вызвать колебания маятника, можно либо толкнуть шарик, либо отведя в сторону, отпустить его.
Вынужденными называются такие колебания, в процессе которых система подвергается воздействию внешней периодической силы. Примером служат колебания моста, возникающие при прохождении по нему людей, шагающих в ногу. Автоколебания, как и вынужденные колебания, сопровождаются воздействием на колеблющуюся систему внешних сил, однако моменты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой - она управляет внешним воздействием.
Примером автоколебательной системы являются часы, в которых маятник получает толчки за счет энергии поднятой гири или закрученной пружины. При параметрических колебаниях за счет внешнего воздействия происходят периодические измерения какого-либо параметра системы, например, длины нити, к которой подвешен шарик, совершающий колебания.
Рассмотрим механическую систему, положение которой может быть задано одной координатой X (например, расстояние шарика от положения равновесия О (рис. 1).
Рис.1 Математический и пружинный маятник

Потенциальная энергия системы будет функцией одной переменной х: U=U(x). Допустим, что система обладает положением устойчивого равновесия. В этом положении функция U(x) имеет минимум. Условимся координату X и потенциальную энергию U отсчитывать от положения равновесия. Тогда U(0) 0.
Разложим U(x) в ряд по степеням х, причем ограничимся рассмотрением малых колебательных систем, причем высшими степенями можно будет пренебрегать.
По формуле Маклорена |
|
|
|
|
|
|
2 |
... |
|
U(x) U(0) U (0)x 1 |
2U (0)x |
|
|
|
|
|
|
|
(0) . |
Учтем, что U(x) при х=0 имеет минимум, U (0) (0),U(0) |
||||
Введем обозначения: U |
|
|
|
|
(0) K 0(K 0). Тогда |
|
|||
|
|
|
U(x) 1 2kx2 |
(1) |
Сила F, действующая на систему, связана с потенциальной энергией соотношением:
F dU dx kx
dx kx
Данное выражение соответствует упругой силе деформированной пружины (рис.1). Здесь k - жесткость пружины. Легко показать, что при малых колебаниях, сила, действующая на маятник, (рис.1) такого же вида. Действительно, из анализа можно написать приближению пропорцию
Md F l x |
(3) |
|
|
С учетом того, что сила направлена в положение равновесия, из соотношения (3) |
|
получим |
|
F (md l)x kx |
(2’) |
где k=md/l. Силы вида (2) независимо от их природы называют квазиупругими. Запишем уравнение движения (второй закон Ньютона) для рассмотренных систем
F ma mx или ma mx |
(4) |
Введя обозначение ω02 = k/m, преобразуем уравнение следующим образом:
x 02 x 0 |
(5) |
Итак, в отсутствие силы трения движение под действием квазиупругих сил описывается дифференциальным уравнением (5). Решением уравнения является выражение
x Acos(w0 t L) |
(6) |
где А - амплитуда колебания, L - начальная фаза. Итак, смещение х изменяется со временем t по закону косинуса. Следовательно, движение системы, находящейся под действием силы вида F kx, представляет собой гармоническое колебание.
Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания затухают. В простейшем случае, сила сопротивления Fc пропорциональна величине скорости х’:
Fc rx (7)
Здесь r - постоянная, называемая коэффициентом сопротивления. Знак минус обусловлен тем, что сила Fc и скорость х’ имеют противоположные направления.
Уравнение движения системы (уравнение второго закона Ньютона) при наличии сил сопротивления имеет вид
|
|
|
rx |
|
|
(8) |
x m kx |
|
|
||||
Применив обозначения |
|
|
||||
|
|
|
|
2 r m, 02 |
k m |
(9) |
перепишем уравнение (8) следующим образом: |
||||||
x |
|
|
2 |
|
(10) |
|
|
2 x |
0 x 0 |
|
|||
Это дифференциальное уравнение описывает затухающие колебания системы. |
||||||
При не слишком большом затухании 0 |
общее решение уравнения (10) имеет вид |
|||||
|
x A e t cos( t l) |
(11) |
|
|||
|
|
0 |
|
|
|
|
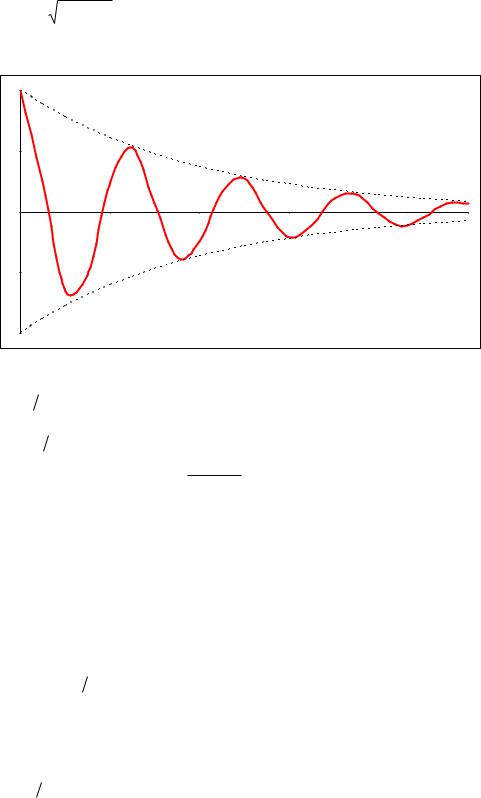
где |
2 |
2 |
частота затухающего колебания, |
A , L -постоянные. В соответствии с |
||
|
0 |
|
|
|
0 |
|
видом движение системы можно приближенно рассмотреть как гармоническое колебание |
||||||
частоты с амплитудой, |
убывающей |
по экспоненциальному закону A(t) A e t |
||||
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
A |
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
10 |
20 |
30 |
40 |
50 |
|
|
|
|
|
|
t |
-0.5 |
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
Скорость затухания определяется величиной |
|
|
||||
r 2m |
(12) |
|
|
|
|
|
которую называют коэффициентом затухания. Период затухающих колебаний равен |
||||||
T 2 . Отношение амплитуды моментам времени отличающихся на период, равно |
||||||
|
|
|
A(t) |
e t |
(13) |
|
|
|
|
A(t T) |
|
|
|
Это отношение называют декрементом затухания, а его логарифм - логарифмическим |
||||||
декрементом затухания: |
|
|
|
|
||
ln |
A(t) |
t (14) |
|
||
|
A(t T) |
|
Закон убывания амплитуды со временем можно записать в виде
A(t) A0e t
Обозначим за τ время, за которое амплитуда уменьшается в е раз, а система успевает
совершить Ne T |
|
|
|
|
|
|
||
|
|
|
|
|
||||
колебаний. Из условия e T e 1получается, что |
|
|
Ne |
1. |
||||
T |
||||||||
|
|
|
|
|
|
|
||
Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за промежуточное время, в течение которого амплитуда уменьшается в е раз.
Для характеристики колебательной системы часто употребляют добротность
колебательной системы |
|
Q Ne |
(15) |
Как видно из ее |
определения, добротность пропорциональна числу колебаний Ne, |
совершаемых системой за время τ, в течение которого амплитуда колебаний уменьшаетеся в е раз.
Описание установки Установка состоит из штатива (рис.4), на котором подвешивается пружина, ее
нагружают грузами разного веса. В качестве шкалы измерения смешения используется масштабная линейка.
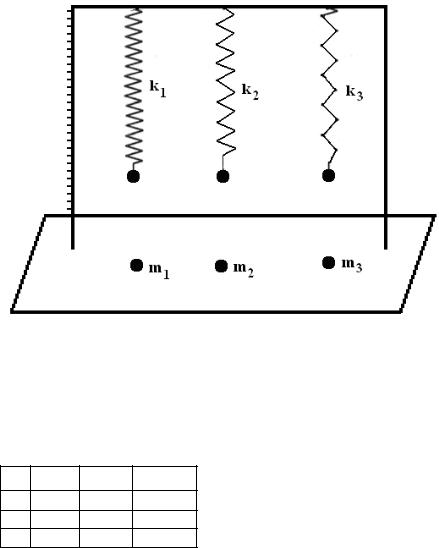
Рис. 4. Экспериментальная установка
Упражнение 1. Определение коэффициента жесткости пружины статистическим методом
Для определения коэффициента жесткости пружины к измеряется длина Δl , на которую растянется пружина при подвешивании к ней груза с массой m. Из условия mg=kΔl, находят k=mg/Δl. Измерения проводят для каждой пружины при трех различных грузах. Результаты заносят в таблицу (для каждой пружины отдельная таблица).
№ m, кг l , м ki , Н/м
1
2
3
Упражнение 2. Нахождение зависимости периода собственных колебаний пружинного маятника от массы груза
Измеряется период Т собственных колебаний пружинного маятника для одной из пружин с коэффициентом жесткости к при разных грузах и строится зависимость Т2 от массы грузаm Для измерения Т выводят груз из положения равновесия примерно 30-50 мм и измеряют секундомером промежуток времени t в течение которого маятник совершит n колебаний n = 1020. Величина T определяется из соотношения T=k/n. Для большей точности следует сделать несколько измерений и взять средний результат. Оцениваются границы до вертикального интервала ΔT с помощью дисперсии.
Упражнение 3. Определение зависимости собственных колебаний пружинного маятника от коэффициента жесткости пружины
Измеряется период собственных колебаний Т пружинного маятника для всех имеющихся пружин при одном и том же грузе (30-50 г) и строится график зависимости Т2 от к. Зная период колебаний системы и массу груза, следует вычислить коэффициент жесткости по формуле к=4π2m/T2 и сравнить с коэффициентом жесткости к, полученным статистическим методом.
Упражнение 4.Определение логарифмического декремента затухания пружинного маятника и коэффициента трения
Для определения логарифмического декремента затухания пружинного маятника груз массы m помещают в сосуд с жидкостью и измеряют период колебаний Т и время t, в течение которого амплитуда колебаний уменьшается до 10 % своей первоначальной величины, т.е. до

At 0,1A0 . Измерения следует проделать для нескольких начальных амплитуд (70,50,30),
причем для каждого значения амплитуды рекомендуется проделать не менее пяти измерений. По данным измерений вычисляют логарифмический декремент из соотношения
|
T |
ln |
A0 |
(17) |
|
|
|||
|
t At |
|
||
Зная , по формуле rT /2m (18)
находят коэффициент силы трения r. Погрешность определения оценивается по формуле:
T ln A0 t At
Контрольные вопросы:
1.Какое движение называется колебательным?
2.Какие колебания называются гармоническими?
3.Какие колебания называются собственными?
4.От чего зависит период собственных колебаний пружинного маятника?
5.Вывести уравнение движения маятника?
6.Что называется коэффициентом жесткости пружин?
7.Какую роль играет сила тяжести в характер колебаний пружинного маятника?
8.Что называется условным периодом затухания: колебаний?
9.Что называется коэффициентом затухания?
10.Что называется логарифмическим декрементом затухания?
11.Как связаны коэффициент затухания и логарифмический декремент?
12.По какому закону изменяется амплитуда затухающих колебаний?
13.Как понимать выражение «сосредоточенная система»?
ЛИТЕРАТУРА
1.Грабовский Р.И., Курс физики; 1974, §10,27, 28, 29, 30; 1980, § 10, 27, 28, 29,30 31. 2.Савельев И.В., Курс физики, т. 1 ,1977, § 14.
Лабораторная работа №20 Определение ускорения силы тяжести с помощью
математического и физического маятников
Принадлежность: универсальный маятник с миллисекундомером (ФПМ -04).
Цель работы: 1. изучить физический и математический маятники и связанные с ними основные физические законы и понятия; 2. научиться с их помощью экспериментально определять ускорение силы тяжести.
Введение Гармонические колебания представляют собой периодический процесс, в котором
смещение системы от положения равновесия происходит с течением времени по закону синуса или косинуса, т.е. по гармоническому закону:
X Asin( t 1) или X Acos( t 2)
Величина А (наибольшее значение отклонения) называется амплитудой колебания, - круговой частотой колебаний. Через промежуток времени T 2 / функции синуса и косинуса проходят через одни и те же значения, т.е. движение повторяется. Этот промежуток времени называется периодом колебаний. Аргумент тригонометрической функции t 1
или t 2 называется фазой колебаний.
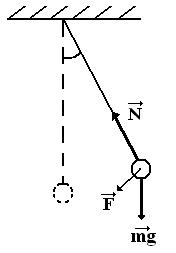
Рассмотрим механическую колебательную систему, состоящую из практически нерастяжимой, очень легкой нити и подвешенного к ней груза массы m, размеры которого малы по сравнению с длиной нити, а масса велика по сравнению с ее массой (рис.1). Такая система ближе всего подходит по своим свойствам к идеальному математическому маятнику.
Математическим маятником называют систему, представляющую собой материальную точку, подвешенную на тонкой невесомой и нерастяжимой нити.
Отклоним грузик от положения равновесия в сторону, а затем отпустим. Грузик будет двигаться к положению равновесия с ускорением х", которое возникло под действием силы, натяжении нити N и силы тяжести P mg .
Достигнув положения равновесия 0, где ускоряющая сила равна нулю, грузик пройдет по инерции положение равновесия и далее будет тормозится той же силой, которая его ускоряла ранее. Затем он остановится и пойдет обратно. Так возникнут собственные колебания маятника. В общем случае колебания маятника не являются гармоническими, но они близки к гармоническим.
Обозначим угол отклонения маятника через и выясним, как он будет изменяться со временем. Сила F , действующая на грузик массой m, составляется из двух сил: тяжести P mg , направленной отвесно вниз, и силы натяжения нити N , направленной вдоль нити к точке подвеса. Последняя перпендикулярна к траектории движения, поэтому тангенциальная составляющая F , действующая вдоль дуги, будет зависеть только от силы тяжести mg и угла отклонения от положения равновесия:
F P sin mg sin (1)
