
- •Контрольные вопросы
- •Тема 2. Последовательности. Предел последовательности
- •2.1. Числовые последовательности
- •2.2. Предел числовой последовательности
- •2.3. Нахождение пределов числовых последовательностей. Число
- •Контрольные вопросы
- •Тема 3. Предел и непрерывность функции
- •3.1. Функциональная зависимость. Основные элементарные функции
- •3.2. Предел функции
- •3.3. Бесконечно малые и бесконечно большие функции
24 25
![]() ,
,
где
![]() .
.
Пример.Даны комплексные числа![]() ,
,![]() .
Найти
.
Найти![]() ,
,![]() ,
,![]() ,
,![]() .
.
Решение.
![]() ,
,
![]() ,
,
![]()
![]() (учли, что
(учли, что![]() ).
).
![]() .
.
Умножая числитель и знаменатель на
сопряженное делителю комплексное число
![]() ,
получим:
,
получим:
![]()
![]() .
.
Контрольные вопросы
1. Какие операции можно выполнить над множествами? Приведите примеры.
2. Из каких чисел состоит множество действительных чисел?
3. В какой форме записывают комплексные числа?
4. Как выполняются действия над комплексными числами?
Тема 2. Последовательности. Предел последовательности
2.1. Числовые последовательности
Под числовой последовательностью
![]() ,
,![]() ,
…,
,
…,![]() ,
… понимают функцию
,
… понимают функцию![]() ,
заданную на множестве
,
заданную на множестве![]() натуральных чисел. Числовая
последовательность обозначается
натуральных чисел. Числовая
последовательность обозначается![]() ,
или
,
или![]() где
где![]() .
.
Последовательность задается формулой ее общего члена. Например,
![]() :
1,
:
1,
![]() ,
,
![]() ,
… ,
,
… ,
![]() ,
…
,
…
В школьном курсе математики изучаются арифметическая прогрессия
![]() ,
,![]() ,
,![]() …,
…,![]() ,
…,
,
…,
и геометрическая прогрессия
![]() ,
,![]() ,
,![]() ,
…,
,
…,![]() ,….
,….
Последовательность называется
ограниченной, если существует такое
число
![]() ,
что для любого
,
что для любого![]() выполняется неравенство
выполняется неравенство![]() .
В противном случае – неограниченной.
Так, последовательность
.
В противном случае – неограниченной.
Так, последовательность![]() ограниченная, а последовательность
ограниченная, а последовательность![]() неограниченная.
неограниченная.
Последовательность
![]() называется возрастающей (неубывающей),
если для любого
называется возрастающей (неубывающей),
если для любого![]() выполняются неравенства
выполняются неравенства![]()
![]() ,
аналогично убывающей (невозрастающей)
,
аналогично убывающей (невозрастающей)![]()
![]() .
Такие последовательности называются
монотонными. Последовательность
.
Такие последовательности называются
монотонными. Последовательность
![]() :
:![]()
не монотонна.
Если все члены последовательности
![]() равны одному и тому же числу
равны одному и тому же числу![]() ,
то ее называют постоянной.
,
то ее называют постоянной.
2.2. Предел числовой последовательности
Числовая последовательность
![]() неограниченно приближается к единице.
В этом случае говорят, что последовательность
неограниченно приближается к единице.
В этом случае говорят, что последовательность![]() стремится к пределу, равному
стремится к пределу, равному![]() .
При этом абсолютная величина разности
.
При этом абсолютная величина разности![]() становится все меньше и меньше, т.е. с
ростом
становится все меньше и меньше, т.е. с
ростом![]() модуль
модуль![]() будет меньше любого, сколь угодно малого
положительного числа.
будет меньше любого, сколь угодно малого
положительного числа.
Число
![]() называется пределом последовательности
называется пределом последовательности![]() ,
если для любого положительного числа
,
если для любого положительного числа![]() найдется такое натуральное числоN,
что при всех
найдется такое натуральное числоN,
что при всех![]() Nвыполняется неравенство
Nвыполняется неравенство![]() .
В этом случае пишут
.
В этом случае пишут
![]()
и говорят, что последовательность
![]() имеет предел, равный
имеет предел, равный![]() .
Также говорят, что последовательность
.
Также говорят, что последовательность![]() сходится к
сходится к![]() .
Последовательность не может иметь два
различных предела.
.
Последовательность не может иметь два
различных предела.
Используя логические символы: квантор
общности
![]() (для любого) и квантор существования
(для любого) и квантор существования![]() (найдется), символ равносильности
(найдется), символ равносильности![]() ,
определение предела последовательности
можно коротко записать так:
,
определение предела последовательности
можно коротко записать так:
![]()
![]() (
(![]()
![]() N:
N:![]() n>N
n>N![]()
![]() ).
).
Геометрический смысл определения
предела последовательности состоит в
следующем. Неравенство
![]() равносильно неравенствам
равносильно неравенствам![]() или
или![]() ,
которые показывают, что член
,
которые показывают, что член![]() находится в
находится в![]() – окрестности точки
– окрестности точки![]() ,
начиная с некоторого номера
,
начиная с некоторого номера![]() .
.
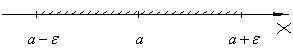
Ясно, что чем меньше
![]() ,
тем больше числоN, и
в любом случае внутри
,
тем больше числоN, и
в любом случае внутри![]() – окрестности точки
– окрестности точки![]() – находится бесконечное число членов
последовательности, а вне нее может
быть лишь конечное их число.
– находится бесконечное число членов
последовательности, а вне нее может
быть лишь конечное их число.
Последовательность, не имеющая предела,
называется расходящейся. Для постоянной
последовательности
![]()
![]() .
Всякая монотонная ограниченная
последовательность имеет предел (теорема
Вейерштрасса).
.
Всякая монотонная ограниченная
последовательность имеет предел (теорема
Вейерштрасса).
2.3. Нахождение пределов числовых последовательностей. Число
Для вычисления пределов последовательностей
используют следующую теорему. Если
![]() ,
,![]() ,
то
,
то
![]() ,
,![]() ,
,![]() ,
,
где
![]()
Например, найти пределы следующих последовательностей.
1.
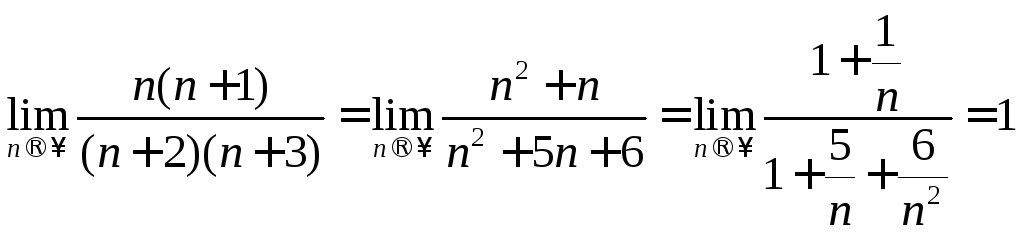 (так как
(так как![]() при
при![]() ).
).
2.
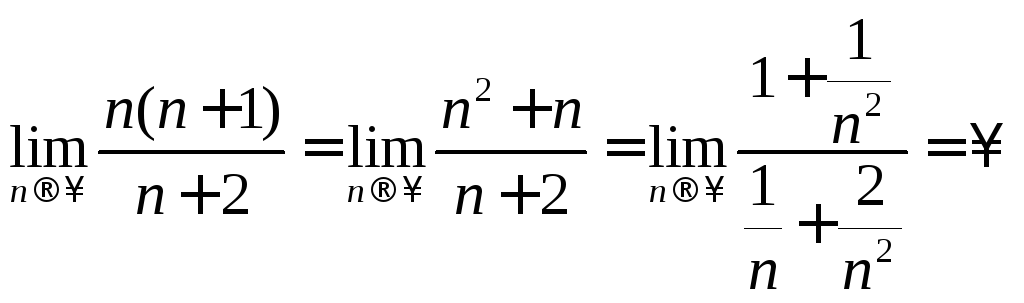 .
.
3.
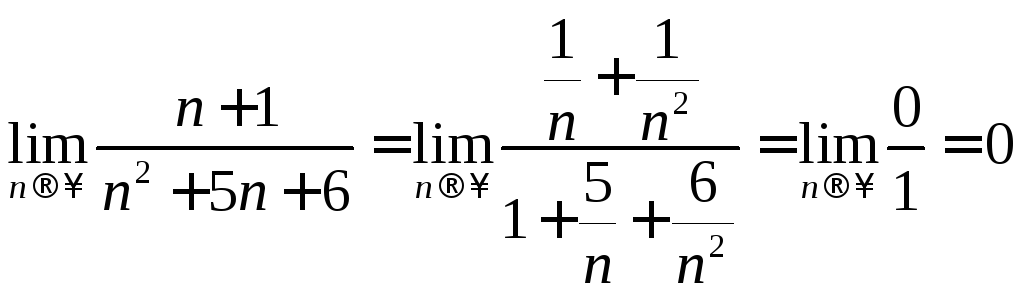 .
.
4.
![]() .
.
Последовательность с общим членом
![]() имеет предел, обозначаемый обычно буквойе, т.е.
имеет предел, обозначаемый обычно буквойе, т.е.![]() .
Число
.
Число![]() иррациональное, его приближенное
значение равно 2,72 (е = 2,718281828459045…).
иррациональное, его приближенное
значение равно 2,72 (е = 2,718281828459045…).
Это
число играет важную роль в математике
и ее приложениях. График функции
![]() получил название экспоненты. Широкое
применение имеет логарифм по основанию
получил название экспоненты. Широкое
применение имеет логарифм по основанию![]() ,
называемый натуральным логарифмом
,
называемый натуральным логарифмом![]() .
К числу
.
К числу![]() приводит анализ таких процессов, как
рост населения, размножение бактерий,
распад радиоактивных элементов.
приводит анализ таких процессов, как
рост населения, размножение бактерий,
распад радиоактивных элементов.
В
экономике число
![]() используется, например, в задаче о
непрерывном начислении процентов. Пусть
вклад в банк
используется, например, в задаче о
непрерывном начислении процентов. Пусть
вклад в банк![]() денежных единиц и банк выплачивает
ежегодно
денежных единиц и банк выплачивает
ежегодно![]() годовых. Найти размер вклада
годовых. Найти размер вклада![]() через
через![]() лет. При использовании простых процентов
ежегодно вклад увеличивается на величину
лет. При использовании простых процентов
ежегодно вклад увеличивается на величину![]() ,
т.е.
,
т.е.
![]() .
.
В
финансовых расчетах возникает
необходимость применять сложные
проценты, когда размер вклада увеличивается
в одно и то же число
![]() раз, т.е.
раз, т.е.
![]() ,
,
![]() ,
… ,
,
… ,![]() .
.
Если
начислять проценты не один раз в год,
а
![]() раз, то
раз, то
![]() .
.
Пусть
они начисляются непрерывно
![]() (квартал, месяц, каждый день, час и т.д.).
Тогда
(квартал, месяц, каждый день, час и т.д.).
Тогда
![]() .
.
Эта формула при непрерывном начислении процентов, используется при анализе различных финансовых задач.
