
Sbornik_ispr
.pdf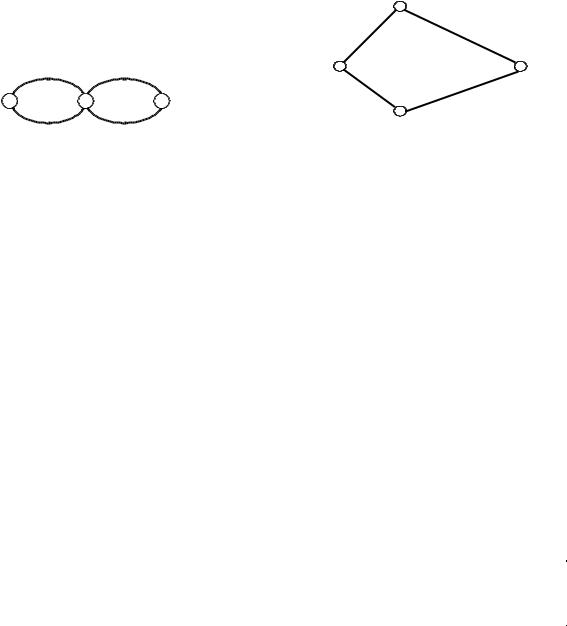
где Р st( lm =1) - надежность связи при |
lm =1, т.е.вершины l и |
|
m слиты в одну точку (рис. 2.10); |
|
|
Р st( lm =0) |
- надежность связи при lm =0, т.е. из графа изъято |
|
ребро между l и m (рис. 2.11). |
|
|
|
|
l |
|
|
t |
l |
s |
|
|
|
|
s |
t |
|
|
|
m |
m
Рис. 2.10. Структура графа, приведенного Рис. 2.11. Структура графа, на рис. 2.9 при lm =1. приведенного на рис. 2.9
при lm =0.
Метод последовательного разложения позволяет свести расчет структурной надежности непараллельно-последовательного графа к расчету структурной надежности параллельно-последовательных графов.
Значения коэффициентов готовности каналов тональной частоты (ТЧ) и
основных цифровых каналов (ОЦ) на телефонных сетях Российской Федерации приведены в таблице 2.2.
|
|
|
Таблица 2.2 |
|
|
|
|
Тип телефонной |
Максимальная |
Значения коэффициентов готовности для |
|
сети |
протяженность |
каналов |
|
|
канала, км |
|
|
|
|
ТЧ |
ОЦ |
|
|
|
|
Междугородная |
12500 |
0,92 |
0,98 |
|
|
|
|
Внутризоновая |
1400 |
0,99 |
0,99 |
|
|
|
|
Местные (городские |
200 |
0,997 |
0,997 |
и сельские) |
|
|
|
21
4. Варианты заданий
Варианты заданий представлены на рис.1.4 и 1.5 и в таблицах 1.1 и 1.2 по теме 1: «Структурные матрицы сетей и операции с ними».
5.Содержание отчета
1.Вариант задания графа сети и исходные данные.
2. |
Схема всех путей ранга r 3 от вершины |
i к вершине j. |
3. |
Расчет структурной надежности графа при связи от вершины i к |
|
|
вершине j при использовании всех путей |
ранга r 3 при условии, |
|
что коэффициенты готовности всех ребер графа одинаковы и равны |
|
|
0,9. |
|
|
Литература |
|
1. |
Ушаков И.А. Курс теории надёжности систем. Учебное пособие для |
|
ВУЗов. – М.: Дрофа, 2008. – 239 с.
2. Нетес В.А. Основы теории надёжности: Учебное пособие/МТУСИ. –
М.,2006.
Тема 3
Алгоритм Дейкстры поиска кратчайшего пути
1. Цель работы
Изучить и практически освоить алгоритм Дейкстры поиска кратчайшего
пути.
2.Задание
1.Изучить алгоритм Дейкстры.
2.Используя алгоритм Дейкстры, найти кратчайший путь из вершины s к
вершине t.
22
Исходные данные для расчета по двадцати вариантам представлены в таблице 3.2. Вариант задаётся преподавателем: может выбираться, например,
по последней цифре номера зачетной книжки или по номеру в групповом журнале.
3. Теоретическая часть
Задача поиска кратчайшего пути наиболее часто встречается на практике.
Под кратчайшим путем может пониматься путь минимальной длины,
минимальной стоимости или по любым другим весовым коэффициентам,
присваиваемым ветвям (ребрам) графа.
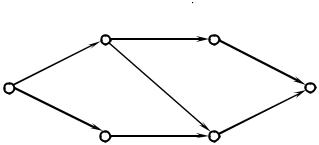
Пусть задан ориентированный граф (рис. 3.1.).
1 |
c12=3 |
2 |
cs1=4 |
|
c2t=2 |
s |
c14=2 |
t |
|
|
|
cs3=3 |
|
c4t=2 |
3 |
c34=3 |
4 |
Рис. 3.1. Ориентированный граф
Пусть длина каждого ребра выражается неотрицательным числом c i j ≥ 0 .
Если из i в j нет ребра, то c i j = ∞. |
|
|
|
|
δi |
|
|
Алгоритм основан на приписывании узлам временных δi |
или |
|
|
|
|
||
|
|
||
постоянных весов, равных длине кратчайшего пути из s в t, |
включающего |
||
только вершины с постоянными весами. |
|
|
|
Алгоритм поиска кратчайшего пути из s в t включает следующие три
шага.
Шаг 1. Постоянный вес вершины s = 0 и временные веса δj = ∞, для всех j s. Положим i=s, где i-номер последней вершины с постоянным весом.
23
Шаг 2. Для каждой вершины с временным весом пересчитываем
величину δj |
по следующему выражению |
|
|
|
|
j = min j ; i |
+ cij |
. |
|
Присвоим вершине, для которой величина δj |
является наименьшей, |
|||
постоянный вес. Положим |
i=j. |
|
|
|
Шаг 3. |
Если i=t, |
то кратчайший |
путь |
найден. В противном случае |
переходим к шагу 2.
Алгоритм Дейкстры позволяет построить дерево кратчайших путей из вершины s во все вершины исходного графа. Для этого шаг 3 нужно изменить следующим образом: если всем вершинам приписаны постоянные веса, то дерево кратчайших путей с корнем в вершине s найдено. В противном случае перейти к шагу 2.
Пример реализации алгоритма для графа, приведенного на рис. 3.1.
Первая итерация |
|
|
|
Шаг 1. Присваиваем вершине s постоянный вес |
S |
= 0 остальным |
|
|
|
|
|
вершинам присваиваем веса δj = ∞ |
j=1, 2, 3, 4, t (j s). |
|
|
Принимаем i=s; i равно номеру вершины с последним постоянным
весом.
Шаг 2. Рассчитаем веса остальных вершин:
1 = min 1 ; s + cs1 = min ∞, 0+4 = 4.2 = min 2 ; s + cs2 = min ∞, 0+∞ = ∞.3 = min 3 ; s + cs3 = min ∞, 0+3 = 3.
4 = ∞.t = ∞.
24

Минимальный вес имеет вершина 3, ей приписываем постоянный вес
3 =3.
Положим i=3.
Шаг 3. Так как i = 3 t, то переходим к шагу 2.
Текущее дерево имеет следующий вид:
s |
3 |
3 |
Вторая итерация
Шаг 2. Так как найдено новое значение i =3 t, то пересчитываем временные веса остальных вершин.
1 = min 1 ; 3 + c31 = min 4, 3+∞ = 4.2 = min 2 ; 3 + c32 = min ∞, 3+∞ = ∞.4 = min 4 ; 3 + c34 = min ∞, 3+3 = 6.
t = ∞.
Минимальный вес имеет вершина 1. Приписываем ей постоянный вес
1 = 4. Положим i =1.
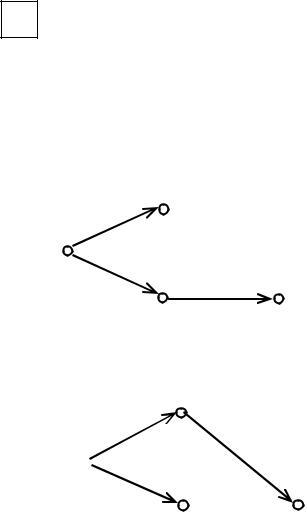
Шаг 3. Так как i = 1 t, переходим к шагу 2.Текущее дерево путей
имеет следующий вид:
1
4
S
3
3
25
Третья итерация
Шаг 2. Так как найдено новое значение i=1 t, то пересчитываем
временные веса вершин.
2 min 2 ; 1 + c12 min ;4 min 4 ; 1 + c14 = min ;t min t ; 1 + c1t .
Минимальный вес имеет вершина 4. Приписываем ей постоянный вес
4 = 6.
Положим i = 4.
Шаг3. Так как i = 4 ≠ t, переходим к шагу 2.
Текущее дерево путей имеет следующий вид:
1
4
s
3
3 |
3 |
4 |
Или
1
4
2
s 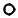
3
3 |
4 |
Так как из вершины s в вершину i = 4 имеется два пути с одинаковым весом, то из двух путей можно выбрать любой (в дальнейших расчетах выбран первый).
26
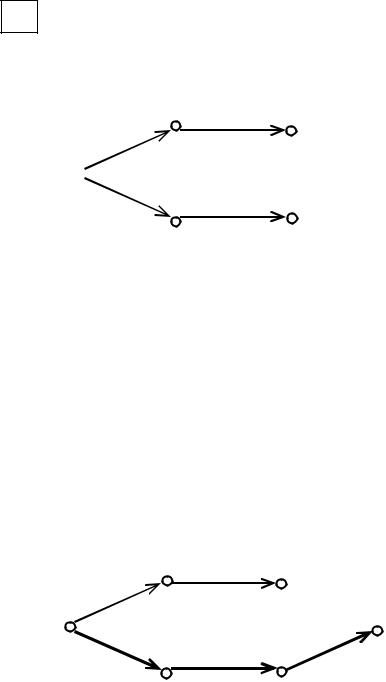
Четвертая итерация
Шаг 2. Так как найдено новое значение i =4 t, то пересчитываем
временные веса вершин.
2 min 2 ; 4 + c42 min ;
t min 2 ; 4 + c4t min .
Минимальный вес имеет вершина 2. Присваиваем ей постоянный вес
2 = 7. Положим i = 2.
Шаг 3. Так как i = 2 t, переходим к шагу 2.
Текущее дерево путей имеет следующий вид:
4 1 3 2
S 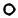
3 |
|
|
||
3 |
3 |
4 |
||
|
||||
|
Пятая итерация. |
|
|
|
|
Шаг 2. Так как найдено |
новое значение i =2 t, то |
||
пересчитываем временные веса вершин. |
||||
|
|
t = min t ; 2 |
+ c2t = min 8, 7+2 = 8. |
|
|
|
Минимальный вес имеет вершина t t = 8. Положим i = t. |
||
|
Шаг 3. Так как i = t, |
алгоритм завершен. Кратчайший путь имеет вес |
||
|
t |
= 8. Окончательное дерево путей имеет следующий вид: |
||
|
|
|
|
|
1 |
3 |
2 |
||
|
|
|
|
|
4 |
|
|
||
|
|
S |
|
t |
3 |
|
2 |
||
3 |
3 |
4 |
||
27
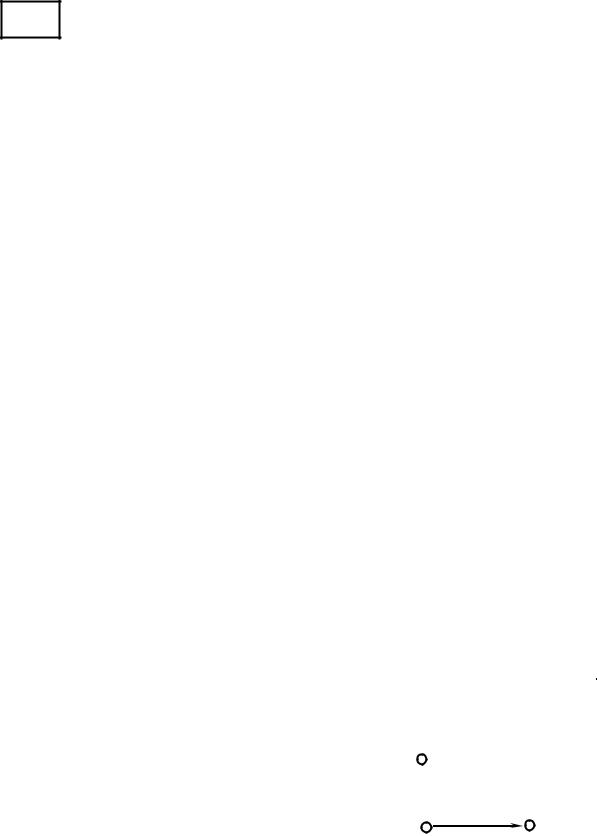
Таким образом, из вершины s в вершину t найден кратчайший путь с весом, t =8 равным 8 .
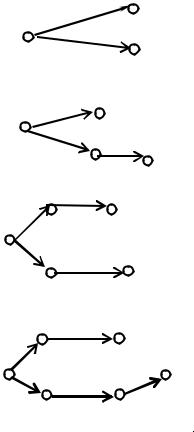
При расчетах веса узлов и вид текущего дерева на каждой итерации заносятся в таблицу 3.1.
Литература
1.Филлипс Д., Гарсиа-Диас А. Методы анализа сетей. – М.: Мир, 1984.
2.Теория сетей связи / Под ред. В.Н. Рогинского. – М., Связь, 1981.
3.Форд Л.Р., Фалкерсон. Потоки в сетях. – М. Мир, 1966.
4.Майника Э. Алгоритмы оптимизации на сетях и графах: Пер. с англ. – М.:
Мир, 1981.
4. Варианты заданий
Исходные данные для расчета по двадцати вариантам представлены в
таблице 3.2.
5.Содержание отчёта
1.Описание процедуры расчета по итерациям и шагам (при ручном
расчете); текст программы, структурная схема программы и результаты расчета
(при проведении расчетов с помощью ПЭВМ).
2.Исходный граф и длина ребер.
3.Таблица итераций.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ ите- |
|
|
|
|
Веса узлов графа |
|
|
Текущее дерево |
|||||||
рации |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
1 |
|
2 |
3 |
|
|
4 |
t |
|
|
|||
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
∞ |
|
∞ |
|
|
∞ |
∞ |
∞ |
|
|
|||
i = S |
|
|
|
|
|
s |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
4 |
|
∞ |
|
|
|
|
|
∞ |
∞ |
|
|
|
0 |
|
|
|
|
3 |
|
|
|
|
|||||
i = 3 |
|
|
|
|
|
|
|
s 3 |
3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
0 |
|
|
|
4 |
|
|
|
|
|
∞ |
|
3 |
|
|
∞ |
|
|
∞ |
|
s |
|
|
|||||||||
i = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
1 |
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
4 |
|
|
|
7 |
|
|
|
3 |
|
|
6 |
|
|
|
|
∞ |
|
s |
|
|
||||||||
i = 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
411 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. |
|
0 |
|
|
|
|
|
4 |
|
|
|
|
|
7 |
|
|
|
3 |
|
|
6 |
|
|
|
|
∞ |
|
|
|
2 |
||||
i = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
0 |
|
|
|
|
|
|
4 |
|
|
|
|
|
7 |
|
|
|
3 |
|
|
6 |
|
|
|
|
8 |
|
|
|
|
|
|
|
i = t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
2 t |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29

Таблица 3.2
№ |
Вид |
графа |
|
|
|
|
Веса |
|
рёбер |
|
|
||
Вар. |
|
|
графа |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
S1 |
12 |
24 |
14 |
13 |
|
S3 |
3t |
4t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
7 |
13 |
7 |
9 |
10 |
|
5 |
12 |
5 |
|
S |
|
2 |
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
6 |
10 |
6 |
8 |
7 |
|
7 |
18 |
4 |
|
|
|
|
|
|
|||||||||
|
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
3. |
|
|
5 |
5 |
4 |
7 |
6 |
|
9 |
8 |
2 |
||
|
|
|
|
||||||||||
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
t |
|
5 |
3 |
2 |
4 |
8 |
|
11 |
4 |
10 |
5. |
|
|
10 |
4 |
4 |
3 |
7 |
|
15 |
3 |
7 |
||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ |
|
|
|
|
S1 |
12 |
23 |
S3 |
34 |
|
45 |
3t |
5t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
5 |
7 |
3 |
9 |
11 |
|
2 |
6 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
S |
|
|
2 |
9 |
3 |
5 |
7 |
3 |
|
2 |
10 |
4 |
|
|
|
|
||||||||||
|
|
|
|
|
|||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
8. |
4 |
|
|
|
7 |
2 |
4 |
2 |
7 |
|
8 |
6 |
2 |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
9. |
|
|
7 |
2 |
3 |
5 |
9 |
|
1 |
4 |
8 |
||
|
|
|
|
||||||||||
|
5 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. |
|
|
|
|
7 |
2 |
1 |
10 |
2 |
|
1 |
7 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30
