07-Теплопроводность

07-Теплопроводность 1

07-Теплопроводность

1.Уравнение Фурье. Условия однозначности.

Задача расчета нагрева и охлаждения твердых тел решается с помощью дифференциального уравнения Фурье (дифференциальное уравнение второго порядка в частных производных).

Т а 2Т а х2Т2 у2Т2 z2Т2

Это уравнение имеет бесчисленное множество решений, соответствующие бесчисленному множеству, то есть классу явлений теплопроводности. Чтобы из этого множества решений выделить одно решение, соответствующее единственному решению данного класса, нужно задать условие однозначности, которые состоят из:

o Геометрических условий, определяющих форму и размеры тела. o Физических параметров материала и среды.

oНачальных условий, описывающих распределения температуры в некоторый момент времени.

oГраничных условий, характеризующих тепловое взаимодействие окружающей среды с поверхностью тела.

Начальные и граничные условиями называют краевыми условиями задачи. Существует четыре способа задания граничных условий:

1.Граничные условия первого рода. Задается распределения температуры по всей поверхности тела и изменения этого распределения во времени Тпов=f(x,y,z,t).

2.Граничные условия второго рода. Задается распределения плотности теплового потока по всей поверхности тела и изменения этого распределения во времени qпов=f(x,y,z,t).

3.Граничные условия третьего рода. Задаются температура окружающей среды и закон теплообмена между средой и поверхностью тела. Этот способ задания граничных условий наиболее общий и часто встречающийся на практике. По существу задается некоторая связь между известной температурой среды и неизвестными температурами на поверхности тела и градиента перепада температуры в теле. Математической формулировкой граничных условий третьего рода в случае КТО на поверхности есть:

07-Теплопроводность 2

Т Т Тпов Тцен , где Тпов задаем.

х

ГУ 4 рода.

ГУ 4 рода соответствуют теплообмену поверхности тела с окружающей средой ( теплообмен в пограничном слое при конвективном теплообмене). Среда отдаёт пограничному слою теплоту, которая конвекцией передаётся поверхности и дальше телу.

ГУ 4 рода.

Тпов ( ) Тсреды ( ) пов

Уравнение Фурье совместно с условиями однозначности дают полную математическую формулировку конкретной задачи теплопроводности.

Поставленная задача может быть решена аналитическим, численным или экспериментальным путём.

В результате аналитического решения находится функция температуры от координат x, y,z,

Т=f(x,y,z)

которая должна удовлетворять самому дифференциальному уравнению теплопроводности (оно при подстановке в него этой функции должно обращаться в тождество), а также НУ и ГУ.

По теореме единственности решения, если некоторая функция температуры от координат и времени удовлетворяет самому уравнению, а также НУ и ГУ, то она является единственным решением этой задачи.

2.Решение уравнения Фурье при ГУ 3 рода.

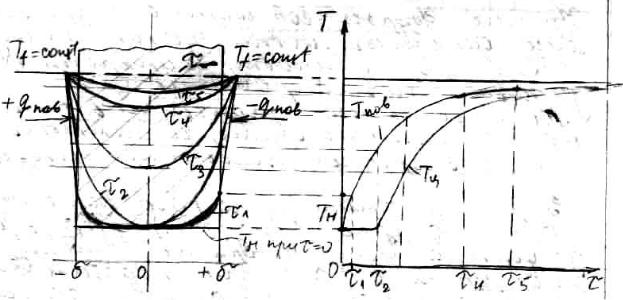
Рассмотрим одномерную задачу (для неограниченной пластины).

07-Теплопроводность 3

Неограниченная пластина, толщиной 2δ, нагревается (или охлаждается) за счёт конвекции от окружающей среды с температурой Т f const

Вначальный момент времени (τ=0) темпе6ратура пластины по толщине одинакова Тн const .

Впроцессе нагрева температура в любой точке пластины будет увеличиваться, стремясь к температуреТ f .

Тн Т f

араспределение температуры по сечению при этом будет выравниваться.

Математическая формулировка задачи.

Для определения функции Т(х,τ) имеем уравнение теплопроводности.

Знак (+ ) перед левой частью ГУ условию на левой поверхности пластины, где х=-д, т. е. когда направление теплового потока совпадает с положительным направлением оси х. А знак (-) – условию на правой поверхности пластины при х=+д, когда тепловой поток направлен в противоположную сторону оси х.

Для решения этой задачи воспользуемся методом разделения переменных.

Сущность его заключается в том, что решение уравнения (1) в виде произведения 2 функций.

Ф зависит от координаты х. П – от координаты ф.

Фурье равен нулю, а это значит время равно нулю.

n Сn cos( n X) (17)

n 1

Данное выражение представляет собой разложение величины n в ряд с заданными значениями n , которое определяется уравнением (14).

Используя уравнение (17), можно показать, что сos( n X) и сos( m X) ( m - любое характерное число, выбранное из бесконечного множества значенийт )являются ортогональными функциями, что означает если

cos( n X) cos( m X)dx 0

при любых значениях n не равных значениям m, то этот интеграл равен нулю. И только при n=m является величиной конечной.

Используем это обстоятельство для определения значения Сn. Для чего умножим обе части выражения (17) на сos( n X) и проинтегрируем по х в пределах толщины пластины, и поменяем порядок суммирование и интегрирование и получим выражения

n cos( m X)dx Сn соs( m X) cos( n X)dx

n 1

В правой части последнего выражения все интегралы равны нулю кроме одного, соответствующему случаю n=m. Поэтому это выражение получает вид:

Следовательно, задача решена, так как из (19) можно найти значение избыточной теплоты, а значит и абсолютные температуры в любой точки пластины в любой момент времени. В решении (19) все независимые переменные фигурируют в безразмерном виде. Роль координаты играет безразмерная величина X x , а роль времени – число Фурье. Поэтому

логично искомую функцию, то есть избыточную температуру, представить в

07-Теплопроводность 7

безразмерном виде. Для этого нужно разделить обе части уравнения (19) на начальную избыточную температуру n , которая известна из начальных условий, тогда получим решение задачи в безразмерном виде:

- относительная безразмерная избыточная температура. Общий вид этого решения расписан так:

f (Bi;Fo;X) (21)

В (21) Fo и Х безразмерные независимые переменные, а Bi – параметр задачи. Термин «безразмерное время», относящееся к ..., для пластин различной толщины и с различными коэффициентами теплопроводности, но при одинаковых значениях критерия Био, температурные кривые построены в координатах f (X) будут совпадать при равенстве чисел Фурье, то есть не

......... те же моменты времени, а сходственные, которые определяются из равенства чисел Фурье. Конкретный вид решения (20) получим для неограниченной плоской пластины, но принципиально в таком же виде, то есть в виде уравнения (21) получаем решения и для тел любой другой геометрической формы. Изменяется только смысл вкладываемый в понятие «характерный размер тела». В случае цилиндра и шара роль характерного размера играет радиус.

Рассмотрим физический смысл критерия Био. Для чего представим его в

характеризует интенсивность внутреннего теплообмена между поверхностями тела и его внутренними слоями. Критерий Био можно

том, что характер распределение температуры по объему нагреваемого или охлаждаемого тела определяется величиной критерия Био. Чем больше Био, тем больше интенсивность внешнего теплообмена по сравнению с интенсивностью внутреннего. Поэтому большему значению Био соответствует меньшая равномерность распределения температуры по объему тела.

Для выявления влияния Био не процесс нагрева (охлаждения) тела, сделаем анализ решения (20) при очень малых значениях, Био стремится к нулю, и при очень больших значениях, Био стремится к бесконечности.

При Био, стремящемуся к нулю.

Такие тела называют «тонкими» в тепловом отношении телами. Угловой

07-Теплопроводность 9

температуры по объему тела на протяжении всего периода нагрева или охлаждения тела, так как в выражении (23) не зависит от Х. Получаем, что температура во всех точках тела растет или падает во времени по экспоненциальному закону.

«Тонкими» в тепловом отношении телами, которые нагреваются или охлаждаются по всему объему, называются тела, у которых Bi 0.25. При нагреве «тонких» тел лимитирующим звеном в процессе нагрева является внешний теплообмен.

Лекция 14

3. Решение уравнения Фурье для твердого тела при граничных условиях первого рода

Случай означает, что интенсивность внешнего теплообмена бесконечно велика по сравнению с интенсивностью внутреннего теплообмена. Для тех конечных размеров, у которых означает, что, а это приводит к тому, что температура поверхности тела очень быстро (почти мгновенно) становится равной температуре среды, которая задана и постоянна.

мгновенно принимает температуру среды и получаем задачу с граничными условиями первого рода, когда температура поверхности постоянна.

Решение этой задачи получим как частный случай решения (20) с задачей граничного условия третьего рода при Bi .

Характеристическое уравнения (14), в этом случае, принимает вид ctg 0, следовательно, прямая линия на графике совпадает с осью абсцисс и значение

Так как в решении (25) n определяется последовательностью (24), и, следовательно, n f (Bi), то есть при граничных условиях первого рода общий вид решения (25) имеет вид: f (Fo, X)

Вэтом случае Bi не является параметром задачи и лимитирующим звеном

впроцессе нагрева или охлаждения, является внутренним теплообменом.

4. Решение уравнения Фурье при граничных условиях второго рода. Математическая формулировка задачи.

Особенность этой задачи: при граничных условиях первого и третьего родов температурное поле с течением времени стремится к равновесию, то есть температура в любой точке тела стремится к температуре среды при граничных условиях третьего рода или к температуре поверхности при граничных условиях первого рода. Для решения этой задачи введем вместо температуры новую переменную плотность теплового потока q(х, ), связанную с температурой формулой закона Фурье:

q(х, ) дТ(х, )

дх

Продифференцируем по х обе части уравнения дТ а д2Т .

д дх2