модуль 2.15

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный морской технический университет

Предмет:

Физика

Файл:

Замкнем ключ K .

Конденсатор начнет

I . Электрическая энергия конденсатора

катушки, равную

.pdf

Скачиваний:

Добавлен:

18.04.2015

Размер:

581.48 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

ФИЗИКА

Модуль 2.15

ГЛАВА 10 Электромагнитные колебания

1 Электрический колебательный контур

Уравнение колебательного контура
Колебательным контуром называется цепь, состоящая из катушки индуктивности	L

и конденсатора емкости С , в которой могут возникать электрические колебания. Выясним, каким образом в колебательном контуре возникают электрические

колебания.

Пусть вначале верхняя обкладка конденсатора заряжена положительно, а нижняя отрицательно (рис.1, а).

а)

б)

Рис. 1

При этом вся энергия колебательного контура сосредоточена в конденсаторе и равна

	q	2
WCm		m	, где	C	-	емкость	конденсатора.

	2C

разряжаться, и через катушку							L потечет ток
начнет		превращаться				в магнитную энергию

индуктивность катушки. Этот разрядится, ток цепи достигнет энергия колебательного контура

процесс закончится, когда конденсатор полностью максимума (рис. 1, б). В этот момент электрическая равна нулю WC 0 , а магнитная, сосредоточенная в

катушке, максимальна

		LI	2
W		LI	m
W

	Lm	2
		2

. С этого момента ток, не меняя направления, начнет

убывать. Однако он прекратится не сразу – его будет поддерживать ЭДС самоиндукции. Ток будет перезаряжать конденсатор, возникнет электрическое поле, стремящееся ослабить ток. Наконец, ток прекратится, а заряд на конденсаторе достигнет

максимума qm . Энергия колебательного контура вновь сосредоточится в заряженном

конденсаторе и будет равна

WCm

	q	2
		m

	2C

Далее конденсатор начнет разряжаться опять, ток потечет в обратном направлении и т.д. – процесс будет повторяться.

В контуре при отсутствии сопротивления ( R 0 ) будут совершаться строго периодические колебания. В ходе процесса периодически изменяется заряд на обкладках

конденсатора

напряжение на нем

U	C

и ток через катушку

. Колебания

сопровождаются взаимными превращениями энергии электрического и магнитного полей. Если сопротивление проводников R 0 , то помимо колебаний будет происходить

преобразование электромагнитной энергии в джоулеву теплоту.

Сопротивление проводников цепи R принято называть активным сопротивлением. Найдем уравнение колебаний в контуре, содержащем последовательно соединенные

конденсатор С , катушку индуктивности L , активное сопротивление R и внешнюю переменную ЭДС (рис. 2).

Рис. 2

Условимся считать положительным ток, заряжающий конденсатор. Тогда


I	dq		q .
	dt
	dt
Если		I 0		, то и	dq 0	, и наоборот (знак	I	совпадает со знаком	dq ).

Согласно второму правилу Кирхгофа сумма падений напряжения на всех замкнутого контура равна сумме всех электродвижущих сил ( ), действующих Для нашего случая

U R UC S ,

где

U R

- мгновенное напряжение на активном сопротивлении,

мгновенное напряжение на конденсаторе,

- заряд конденсатора,

S	dt
	dt
ЭДС самоиндукции.
Поэтому уравнение (10.2) можно переписать в виде:

(10.1)

элементах

вконтуре.

(10.2)

U C	q	-
	C

L	dI	IR	q
	dt		C

или с учетом (10.1) как

(10.3)

L d 2 q R dq 1 q dt 2 dt C

Это и есть уравнение колебательного контура – линейное уравнение второго порядка с постоянными коэффициентами.

Уравнению можно придать иной вид:

	q 2 q 2 q
		L ,
	0

где введены обозначения

2 RL , 02 LC1 .

(10.4)

дифференциальное

(10.5)

(10.6)

Величину	0	называют собственной частотой контура,	- коэффициентом
затухания.
Если 0	, то колебания называют свободными.
При R 0	они будут незатухающими.

При R 0 - затухающими.

Рассмотрим последовательно все эти случаи.

2 Свободные электрические колебания в LC - контуре

Если в контуре нет внешней ЭДС и активное сопротивление R 0 (рис.1, б), то колебания в таком LC контуре являются свободными незатухающими.

Их уравнение – частный случай уравнения (10.4), когда 0 и R 0 ,

	d	2	q	1
L					q 0
	dt		2	C

или

d 2 q	2 q 0
		.	(10.7)
dt 2	0

Уравнение (10.7) хорошо изучено в теории механических колебаний. Решением этого уравнения является функция

q qm cos(0t ) .

(10.8)

Следовательно, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой

			1
	0
			LC

(10.9)

Это частота называется собственной частотой контура. Период свободных незатухающих колебаний

	2
T	2	2 LC	(10.10)
T		2 LC
	0
	0
(формула Томсона).
Напряжение на конденсаторе

U		q	q	m	cos( t ) U		cos( t )
				m
	C	C	C		0	m	0
		C	C

(10.11)

Сила тока в контуре

I dqdt 0 2 qm sin( 0 t ) I m cos( 0 t 2 )

Таким образом, сила тока опережает по фазе напряжение на конденсаторе на

Из формулы (10.11) и (10.12) следует, что

(10.12)

		.
	2	.
	2

U	m

U m

q	m	,


C

I m

I m 0 qm или

I m	L	(10.13)

	C
	C

3 Затухающие колебания в RLC - контуре


Пусть в колебательном контуре имеется емкость								С , индуктивность
сопротивление R						(рис. 3). В этом случае
U R UC S						, или
IR		q	L		dI		или

		C			dt
L	dI		IR	q		0
	dt			C

Рис. 3

Учитывая, что

, а также введя обозначения (10.6), получим

q 0

Что совпадает с уравнением (10.5) при 0 .

Это уравнение совпадает с дифференциальным уравнением механических колебаний.

и активное

(10.14)

затухающих

В случае, когда 2 02 , т.е.

R	2

	2
4L

1 LC

, решение этого уравнения имеет вид

где

qme	t	cos( t ) ,

- частота затухающих колебаний, равная

(10.15)

		1	R	2
2	2	1	R	,	(10.16)
0		LC		,	(10.16)
		LC	2L

qm и - произвольные постоянные, определяемые из начальных условий. График функции q(t) (10.15) показан на рис. 4.

Рис. 4

Период затухающих колебаний равен

T	2	2		T			,
T		0			0		,
					0

		2	2				2
				1

						0
						0

(10.17)

где T0

- период свободных незатухающих колебаний.

Множитель	qm e	t	в (10.15) называют амплитудой затухающих колебаний (показан

на рис. 4 штриховой линией).

Величины, характеризующие затухание:

1) Коэффициент затухания и время релаксации - время, за которое амплитуда

колебаний уменьшается в					e	раз.
qme		qme	1	,
qme		qme		,
отсюда
	1						(10.18)
							(10.18)

2) Логарифмический декремент затухания							. Он определяется как натуральный

логарифм отношения двух значений амплитуд, взятых через период колебания T :

	q			e	t
ln		m				ln e T	T
			(t T )
qm e

Или иначе

(10.19)

N e

где

N e

- число колебаний за время .

Если затухание мало ( 0 ), то 0

и согласно (10.19)

3) Добротность

колебательного контура.

По определению

Чем меньше затухание, тем больше Q .

В случае слабого затухания ( 0 ) согласно (10.21) добротность

Q	1	L
	R	C

Как и для механических колебаний, в случае слабого затухания

(10.20)

(10.21)

(10.22)

(10.23)

	Q 2	W
	Q 2	(W )
		(W )

(10.24)

где W

- энергия, запасенная в контуре в данный момент,

энергии за период колебаний T . В самом деле, энергия W ~ q Отсюда относительное уменьшение энергии за период

( W )

, т.е. W

уменьшение этой

e	2 t	.

	W	W (t) W (t T )	1	e 2 (t T )	1 e
	W	W (t)		e 2 t

Если 1, то e 2 1			2 и W		2 .
				W

2 T 1 e 2

Подставляя в формулу (10.22), получим

	Q
	Q

W (W )

В заключение отметим, что при

апериодический разряд конденсатора. Сопротивление контура, при котором

апериодический, называется критическим RK .

вместо колебаний будет происходить

колебательный процесс переходит в

Значение		RK
откуда

RK 2	L

	C
	C

				R	2
определяется условием	2	2	или	R	K
определяется условием		0	или		2
				4L

4 Вынужденные колебания в RLC

	1	,
	LC	,
	LC

(10.25)

- контуре

Рассмотрим случай, когда в колебательный контур (рис. 2) включена внешняя переменная ЭДС , зависящая от времени по гармоническому закону:

	m	cost
	m

(10.26)

данном случае по второму правилу Кирхгофа

R UC S ,

	IR
	L	dI
		dt

или

d	2	q

dt		2

	q
	C
	C

		L	dI		,
		L	dt		,
			dt
	q					cos t
	C				m	cos t
					m

dq				2
					q			m
								m
dt				0			L
dt							L

cos t

(10.27)

(10.28)

Решение этого уравнения, как известно из математики, представляет собой сумму общего решения однородного уравнения (без правой части, ур. 10.14) и частного решения неоднородного уравнения.

Нас будут интересовать только установившиеся колебания, т.е. частное решение

этого уравнения. Решение уравнения (10.14) содержит экспоненциальный множитель e

(см. формулу 10.15), а при t

, поэтому по истечении некоторого времени

оно практически исчезает. Нетрудно убедиться, что частное решение имеет вид:

q qm cos( t ) ,

(10.29)

где qm -

амплитуда заряда на конденсаторе, - разность фаз между колебаниями

заряда и внешней ЭДС

(10.26).

Определим постоянные qm

и .

Сначала найдем ток

I и затем его выражение подставим в уравнение (10.27).

Продифференцировав (10.29) по t , найдем

I q

sin( t ) q

cos(t

)

Запишем это выражение так:

I I m cos( t ) ,

(10.30)

где Im - амплитуда тока, - сдвиг по фазе между током и внешней ЭДС ,

I m qm

Таким образом,

			.
		2

задача сводится к нахождению

I	m

(10.31)

и	. Для этого представим

исходное уравнение (10.27) в виде:

U L U R UC m cost ,

(10.32)

где слева записана сумма напряжений на индуктивности	L , сопротивлении R	и
емкости C . Таким образом, мы видим, что сумма этих напряжений равна в каждый
момент внешней ЭДС .
Итак,
U R IR RI m cos(t ) ,	(10.33)

U U

		q
		C

L dI dt

q	m	cos(t )			I	m	cos(t


C					C
LI			m	sin( t ) LI				m

		)
	2

cos(t

			)
		2

(10.34)

(10.35)

Векторная диаграмма

Из последних формул видно, что

U R

находится в фазе с током

I ,

U	C

отстает по

фазе от

помощью

на		, а	U L	опережает
	2

векторной диаграммы,

на		. Все это можно наглядно представить с
	2

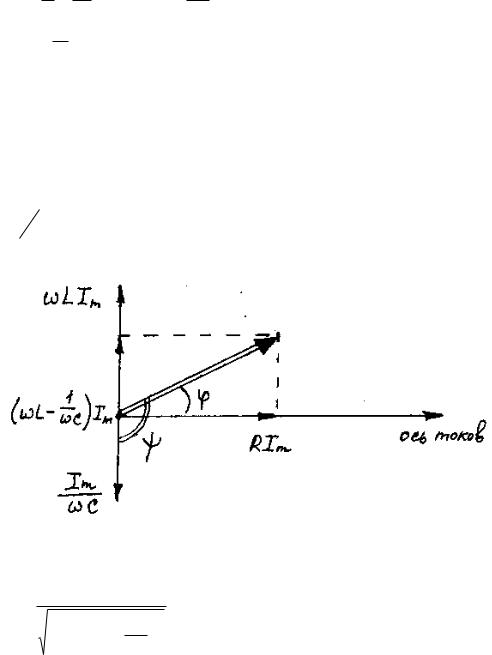
изобразив амплитуды напряжений U Rm RI m ,

UCm I m C , U Lm LI m и их векторную сумму, равную согласно (10.32) вектору величины m (рис. 5).

	m
	m

Рис. 5

Из прямоугольного треугольника этой диаграммы легко получить, что

I m			m		,
			m

				1	2
R	2	L		1
R		L
				C

	L	1
tg		C	.

	R

Задача, таким образом, решена.

(10.36)

(10.37)

Резонансные кривые. Так называют графики зависимостей амплитуды силы тока

амплитуды заряда	qm , а также амплитуд напряжений U Rm , UCm , U Lm от частоты
Резонансные	кривые для силы тока I m () (10.36) показаны на рис. 6.

Рис. 6

I	m

Как видно из выражения (10.36),

I	m

имеет максимальное значение при

	L	1
	L	C
		C

Следовательно, резонансная частота для контура

I	0	1	.
		LC
	рез

Максимум при резонансе тем выше

R	.

2L
Найдем зависимость		qm ( ) .

силы тока совпадает с собственной частотой

(10.38)

и острее, чем меньше коэффициент затухания

q		I	m					m								m
q

	m									2								2	L	1
				2		2	2		1	2	2	R	2	4	2	2		2
				2	R	2	2		1		2		2	4	2
					R			L							L		C			C	2
									C								C			C

				m
				m	L
					L
	R	2				2	2	1
	R					2		1

2			4
2			4
	2					LC		2	2
	L					LC		L C

Учитывая, что				R	, 2	1	,
Учитывая, что					, 2		,
				2L	0	LC
				2L		LC
получим
		m	L
qm			L			.	(10.39)

	( 2	02 )2		4 2 2
	( 2	02 )2		4 2 2

Максимум амплитуды заряда достигается при резонансной частоте

(10.40)

Покажем это

	d ( 2 2 )2						4 2 2
					0								0
					d								0
					d
2(					) 2				8		p		0
2(		2		2	) 2				8	2			0
		2		2						2
		p		0				p	2			p
отсюда p							0		2		0 или
					2			2		2
			2			2			2 2 .
					p			0
Резонансные кривые для													qm ( ) показаны на рис. 7

							Рис. 7
Резонансные кривые для напряжения U ст								на конденсаторе имеют такой же вид,
следовательно,				0	2		.	(10.41)
С		q		0	2		.	(10.41)
				2		2
	рез		рез

Чем меньше , тем ближе резонансная частота к значению 0 .

Форма резонансных кривых определенным образом связана с добротностью Q контура.

В случае слабого затухания, т. е. при 0

Q	U	C	рез

	m
	m
Действительно, при 0					рез	≈ 0 и согласно (10.34) и (10.36)
U C		I m	m	, или
U C		0 C	R 0 C	, или
рез		0 C	R 0 C
рез

(10.42)

U	C		рез	LC	1	L	Q (см. формулу 10.23).
			рез				Q (см. формулу 10.23).
		m		RC	R	C
		m
Таким образом,						добротность контура (при

	0

) показывает, во сколько раз

максимальное внешней ЭДС

значение амплитуды напряжения на конденсаторе превышает амплитуду

m .

Явление резонанса используется для выделения из сложного напряжения нужной составляющей. На этом основана вся техника радиоприема. Для того чтобы радиоприемник принимал интересующую нас радиостанцию, его необходимо настроить, т.е. изменением С и L колебательного контура добиться совпадения его собственной частоты с частотой электромагнитных волн, излучаемых радиостанцией.

5 Переменный ток

Установившиеся вынужденные электрические колебания можно рассматривать как протекание в цепи переменного тока. Под действием внешнего напряжения (оно играет роль внешней ЭДС ).

U U	m	cos t
	m

(10.43)

ток в цепи изменяется по закону

I Im cos( t ) ,

где

(10.44)

							L	1
		U					L	C
I m		U	m		;	tg
			m
							R
				1	2		R
					2
R	2	L
R		L
				C

Стоящее в знаменателе выражение

(10.45)

				1	2
Z	R	2	L	1
Z	R		L
				C

(10.46)

называется полным электрическим сопротивлением или импедансом.

Тогда можно записать закон Ома для амплитудных значений силы тока Im и

напряжения U m в виде:

I		U	m
I

	m	Z
		Z

В выражении (10.46)

- активное сопротивление,

(10.47)

X L	1	называется реактивным сопротивлением.
X L	C

Введем обозначения и названия:

X L L - индуктивное сопротивление,

X C 1 - емкостное сопротивление.

Тогда реактивное сопротивление

X X L X C ,

полное сопротивление Z			R	2	X	2	,
полное сопротивление Z			R		X		,
tg	X	.					(10.48)
tg		.					(10.48)
	R

1 / 21 2 > Следующая >>>

Соседние файлы в предмете Физика

#
18.04.2015611.33 Кб97модуль 1.7.doc
#
18.04.2015507.39 Кб34модуль 1.8.doc
#
18.04.2015979.97 Кб58модуль 1.9.doc
#
18.04.2015352.26 Кб38модуль 2.1.doc
#
18.04.2015530.77 Кб20модуль 2.14.pdf
#
18.04.2015581.48 Кб31модуль 2.15.pdf
#
18.04.2015619.14 Кб32модуль 2.16.pdf
#
18.04.2015558.31 Кб18модуль 2.17.pdf
#
18.04.2015664.93 Кб11модуль 2.18.pdf
#
18.04.2015652.66 Кб17модуль 2.19.pdf
#
18.04.2015601.36 Кб33модуль 2.21.pdf