
модуль 2.16
.pdfФИЗИКА
Модуль 2.16
ГЛАВА 11 Волновые процессы
1 Волны в упругой среде. Типы волн
Волнами называются возмущения, распространяющиеся в среде (или в вакууме) и несущие с собой энергию. Характерное свойство волн состоит в том, что перенос энергии волной осуществляется без переноса вещества.
Основными видами волн являются упругие волны (в частности, звуковые), волны на поверхности жидкости и электромагнитные волны (в частности, световые волны и радиоволны).
Рассмотрим упругую волну. Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебание ее частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с
некоторой скоростью |
- возникает бегущая волна. |
Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают поперечные и продольные волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. Упругие поперечные волны могут возникнуть в среде, в которой возможны деформации сдвига. Действительно, если при сдвиге одного слоя среды по отношению к другому слою возникают упругие силы, стремящиеся возвратить сдвинутый слой в положение равновесия, то в среде могут распространяться поперечные волны. Таким свойством обладают твердые тела. Если в среде возникают силы упругости при деформации сжатия и растяжения, то в такой среде могут распространяться продольные волны. При распространении продольной волны в среде возникают периодически повторяющиеся зоны увеличения и уменьшения концентрации частиц. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как поперечных, так и
продольных волн. |
|
, |
Геометрическое место точек, до которых доходят колебания к моменту времени |
t |
|
|
|
называется фронтом волны (или волновым фронтом). Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической.
Волна, имеющая произвольную форму фронта, всегда может быть представлена в виде суперпозиции плоских волн.
На рис. 1 изображена кривая, которая дает смещение из положения равновесия точек с различными x в некоторый момент времен. Это есть график функции ( x, t) для
времени t . Такой график имеет одинаковый вид и для поперечной и для продольной волны.
1

|
Длина волны - |
это расстояние, на которое |
распространяется волна за время, |
||
равное периоду колебаний частиц среды, т.е. |
|
||||
|
T |
|
(11.1) |
||
|
|
|
|
|
|
где |
- скорость волны, |
T - период колебаний, или |
|
||
|
, |
|
(11.2) |
||
где |
1 |
- частота колебаний. |
|
||
T |
|
||||
|
|
|
|
|
|
|
Можно дать второе определение длины волны |
- это наименьшее расстояние |
|||
между точками среды, колеблющимися с разностью фаз, равной 2 |
(см. рис. 1). |
Рис. 1
2 Уравнение бегущей волны
Уравнением волны называется выражение, |
|
|
колеблющихся частиц как функцию их координат |
x , |
y |
(x, y, z, t) |
|
|
,
которое определяет
z |
и времени |
t |
: |
|
|
|
смещение
(11.3)
Уравнение волны должно быть, таким образом, двоякопериодической функцией. Периодичность во времени обусловлена тем, что каждая точка совершает гармоническое колебание с периодом T . Периодичность по координатам x, y, z следует из того, что
точки, отстоящие друг от друга на расстоянии |
, колеблются одинаковым образом. |
Рассмотрим плоскую волну, |
распространяющуюся вдоль оси |
X . Пусть колебания |
точек, лежащих в плоскости x 0 |
(рис. 2), имеют вид: |
|
(0, t)
A cos( t
)
.
Рис. 2
2

|
Найдем вид колебания точек в плоскости, соответствующей произвольному |
|||||||||||||||||||||||||||||
значению |
|
x . |
|
Для того чтобы пройти путь от плоскости x 0 |
до этой плоскости, волне |
|||||||||||||||||||||||||
требуется время |
x |
|
. Поэтому смещение частицы с координатой x |
в момент времени |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t может оказаться равным смещению частицы в плоскости |
x 0 |
|
в более ранний момент |
|||||||||||||||||||||||||||
времени |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
t t |
x |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
. Разность (t t ) |
|
равна времени , т.е. (t t ) , |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, можно записать, что |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
(0,t |
) Acos (t ) Acos t |
|
|
|
|
. |
|
|
|||||||||
|
(x,t) (0,t ) |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Таким образом, уравнение плоской бегущей волны, распространяющейся вдоль |
|||||||||||||||||||||||||||||
оси |
X , имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
(x, t) |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
(11.4) |
||||||||
|
|
Acos t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
A - амплитуда волны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Зафиксируем некоторое значение фазы в уравнении (11.4), положив |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
t |
|
|
|
|
|
|
|
const . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, получим |
|
|
|
|
|
|
|
|
|||||
|
Продифференцировав по времени |
t |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
1 |
|
dx |
0 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Таким образом, скорость распространения волны в уравнение (11.4) есть скорость |
|||||||||||||||||||||||||||||
перемещения фазы, поэтому ее называют фазовой скоростью. |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Уравнению (11.4) можно придать симметричный относительно x |
и t вид. |
|
|||||||||||||||||||||||||||
|
Для этого введем величину |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
k |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
2 |
|
T |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
которая называется волновым числом.
Тогда уравнение плоской бегущей волны (одномерное) будет иметь вид:
(x, t) A cos( t kx )
(11.6)
Рассмотрим произвольное направление распространение волны.
Пусть колебания в плоскости, проходящей через начало координат (рис. 3), происходят по закону:
(0, t) A cos( t ) .
Возьмем волновую поверхность (плоскость), отстоящую от начала координат на расстоянии l . Колебания в этой плоскости будут отставать от колебаний в плоскости,
проходящей через начало координат, на время |
|
|||||||
|
||||||||
|
|
|
l |
|
|
Acos t k l |
||
Acos |
|
t |
|
|
|
|
||
|
||||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
l |
|
|
||
|
:
3

Пусть |
|
- единичный вектор нормали к волновой поверхности ( |
|||
n |
|||||
вектор любой из точек поверхности. Тогда |
|||||
|
|
|
|
|
|
n |
r r cos l . |
|
|
||
|
|
|
|
||
Заменим в (11.6) l через n |
r , получим: |
||||
|
|
|
|
|
|
|
|
Acos( t k |
|
||
(r , t) |
r ) |
||||
где вектор |
k |
называется волновым вектором, он равен |
|||
|
|
|
|
|
|
k k n |
|
|
|
|
|
|
|
n |
1
),
r
- радиус-
(11.7)
(11.8)
Рис. 3 |
|
|
|
|
Мы получили уравнение плоской |
волны (трехмерное), распространяющейся |
в |
||
|
|
|
|
|
направлении, определяемом волновым вектором k . |
|
|
|
|
Если волна распространяется в поглощающей среде, то интенсивность волны |
||||
постепенно уменьшается – происходит |
затухание волны. Опыт показывает, |
что |
в |
|
однородной среде затухание происходит по экспоненциальному закону: A A0 e |
x |
, где |
||
|
||||
- коэффициент затухания. Тогда уравнение плоской волны, распространяющейся вдоль оси x , примет вид
(x,t) A0 e |
x |
cos(t k x ) , |
|
где |
A0 |
- амплитуда в плоскости |
x
0
.
(11.9)
Уравнение затухающей волны, распространяющейся в произвольном направлении
|
|
|
|
) |
(11.10) |
(r , t) A e n r |
cos( t k r |
||||
|
0 |
|
|
|
|
Теперь найдем уравнение сферической волны.
Рассмотрим точечный источник ( r d - размеров источника). В однородной и изотропной среде волна, порождаемая точечным источником, будет сферической. Пусть фаза колебаний источника равна ( t ) . Тогда точки, лежащие на волновой поверхности
4

радиуса |
r , будут колебаться с фазой |
|
r |
t |
t |
|
|||
|
|
|
|
|
волне требуется время |
r |
|
). |
|
|||
|
|
|
Амплитуда сферической волны, даже в среде постоянной – она убывает с расстоянием по закону
сферической волны имеет вид
Ar cos( t kr ) ,
kr (чтобы пройти путь r , |
||||
без |
поглощения, не |
остается |
||
1 |
r |
. |
Следовательно, |
уравнение |
|
||||
|
|
|
|
|
|
|
|
|
(11.11) |
где |
A - постоянная величина, численно равная амплитуде на расстоянии от |
источника, равном единице.
Уравнение справедливо только при r d - размеров источника.
3 Волновое уравнение
Волновым уравнением называется линейное однородное дифференциальное уравнение в частных производных, описывающее распространение волн в среде (или в вакууме). Установим вид этого уравнения, исходя из уравнения (11.7) плоской гармонической волны:
(x, y, z,t) Acos(t kx x k y y kz z ) ,. |
||
|
|
k x x k y y k z z . |
где учтено, что k |
r |
|
Вторые частные производные функции (11.12) по
x, y, z
и
t
имеют вид
(11.12)
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
Acos(t k |
|
x k |
|
y k |
|
z ) |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
t |
2 |
|
|
|
x |
|
y |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
k x |
; |
2 |
|
|
k y |
; |
2 |
|
k z |
|
|
|
|
|
|
|
|
|
||||||
x |
|
2 |
y |
|
2 |
z |
|
2 |
|||||
2 |
|
|
2 |
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
Сумма производных по координатам
;
2 |
|
2 |
|
2 |
|
k |
2 |
|||
|
|
|
|
|
||||||
x2 |
|
y 2 |
|
z 2 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
Учитывая, что |
k |
2 |
|
|
|
|||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
|
|
|
2 |
|||||
x2 |
y 2 |
|
|
z 2 |
|
|||||
k y2 kz2 k 2 .
(см. 11.5), будем иметь
|
1 2 |
|
||
2 |
t 2 |
(11.13) |
||
|
||||
Это и есть волновое уравнение. Его можно записать в виде
|
|
1 |
|
2 |
|
|
|
|
|||
2 |
t 2 |
, |
|
|
(11.14) |
||||||
|
|
|
|||||||||
где |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
- оператор Лапласа. |
|
|||||
x 2 |
y 2 |
z 2 |
|
||||||||
Нетрудно показать, что решением этого уравнения будет любая функция вида |
|||||||||||
|
|
|
|
|
|
|
) . |
(11.15) |
|||
f (r , t) f ( t kr |
|||||||||||
Отметим, что для |
плоской волны, распространяющейся вдоль оси |
x , волновое |
|||||||||
уравнение имеет вид:
5
|
|
|
1 |
||
2 |
|
|
|
|
|
x |
2 |
|
|
2 |
|
|
|||||
|
|
|
|
||
|
2 |
|
|
|
|
t |
2 |
|
|
|
|
.
(11.16)
4 Скорость упругих волн
1 Скорость волны в твердой среде Рассмотрим тонкий стержень. Под тонким
имеется в виду стержень, толщина которого мала по сравнению с длиной волны |
. При |
малых продольных деформациях стержня справедлив закон Гука: |
|
E , |
|
|
|
(11.17) |
|
где - механическое напряжение (Н/м2), |
E - модуль Юнга (Па), |
|
- относительная |
||
x |
|||||
|
|
|
|
||
деформация среды. Поясним последнее утверждение. |
|
|
|
||
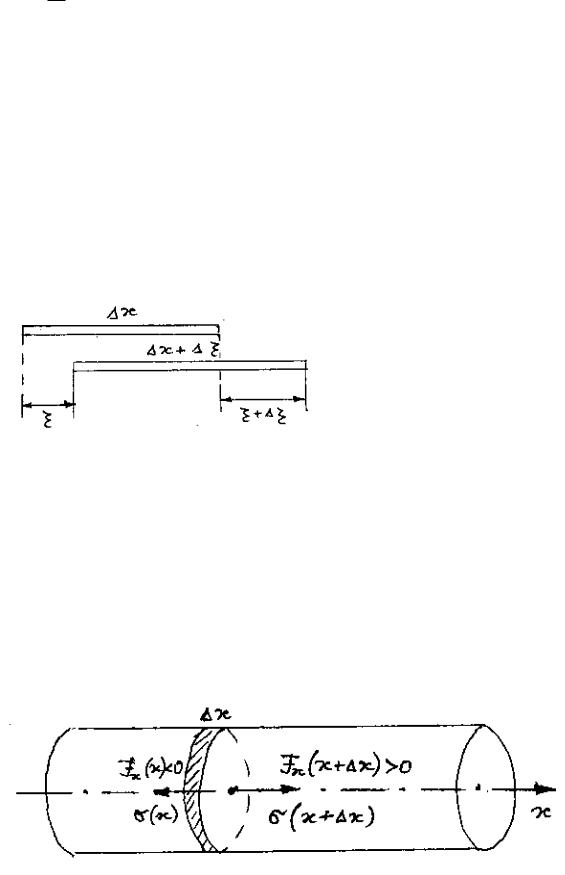
Выделим мысленно малый элемент |
среды x |
в виде цилиндра |
(рис. 4) вдоль |
||
направления распространения волны. При прохождении продольной волны этот элемент
будет смещаться и деформироваться. Например, левый его торец переместится на |
, а |
правый – на ( ) . |
|
Рис. 4
По определению относительная деформация
lim x 0 |
|
|
|
. |
(11.18) |
|||
x |
x |
|||||||
|
|
|
|
|
|
|||
Заметим, что в законе Гука (11.17) и |
- величины алгебраические, и знаки |
|
и |
|||||
всегда одинаковы: при растяжении – положительные, при сжатии – отрицательные. |
|
|
||||||
Рассмотрим малый элемент стержня x в момент, когда при прохождении |
||||||||
волны он оказался, например, в растянутом состоянии (рис. 5). |
|
|
||||||
Запишем II закон Ньютона для элемента |
x : |
|
|
|||||
где
x
|
|
|
|
|
|
|
2 |
|
|
|
|
S |
|
2 |
F |
(x x) F |
(x) |
|
t |
x |
x |
|
|
|
|
|
|
|
- плотность материала стержня, S - площадь его сечения.
Рис. 5
6

В данный момент, как видно из рис. 5, Fx (x x) 0 ; |
Fx (x) 0 . Поэтому |
|
|
||||||||||||||
Fx (x x) Fx |
(x) S (x x) S (x) S |
|
x |
, где учтено, что слева |
Fx |
и |
|||||||||||
x |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
имеют разные знаки. |
|
|
|
|
|
|
|||||||||||
Тогда уравнение движения после сокращения на |
x S примет вид |
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
t |
2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставив E ( см. (11.17)) и учитывая, что |
|
, получим окончательно: |
|||||||||||||||
x |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
t |
2 |
E |
x |
2 |
или |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
||
2 |
|
|
2 |
|
x |
2 |
|
E t |
2 |
|
||||
|
|
|
||
(11.19)
Мы пришли продольная волна,
к волновому уравнению. Итак, в стержне будет распространяться скорость которой равна:
|
E |
|
|
||
|
(11.20)
Можно показать, что скорость поперечных волн в неограниченной изотропной твердой среде
где
|
G |
|
|
|
, |
||
|
|||
|
|
||
G - модуль сдвига среды, - ее плотность. |
|||
(11.21)
2 Скорость звука в жидкостях и газах Формулу (11.20) можно использовать для вычисления скорости продольных волн в
жидкостях и газах. Выясним, что в этом случае играет роль модуля Юнга |
E . |
При продольных волнах в среде возникают сжатия и разряжения отдельных слоев, и закон Гука в данном случае
|
p E |
, |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
где |
p - |
избыточное |
давление |
с относительным |
изменением |
длины |
элемента |
||||||||||
цилиндра |
x , равным |
|
|
. Знак минус связан с тем, что приращение давления p и длины |
|||||||||||||
x |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
противоположны по знаку. |
Умножив числитель |
и знаменатель |
на S - |
площадь |
||||||||||||
поперечного сечения канала, получим |
|
|
|
||||||||||||||
|
p E |
S |
E |
|
V |
, |
|
|
|
(11.22) |
|||||||
|
x S |
V |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где |
V |
- относительное приращение объема. |
|
|
|
||||||||||||
V |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перейдя к пределу, получим |
|
|
|
|
||||||||||||
|
E V |
dp |
. |
|
|
|
|
|
|
|
|
|
(11.23) |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
dV |
|
|
|
|
|
|
|
|
|
|
|||
|
Объем V |
элемента x |
|
и его плотность меняются при прохождении волны, но их |
|||||||||||||
произведение, т.е. масса m |
V const . |
|
|
|
|||||||||||||
7

Отсюда
d |
|
dV |
, значит |
||||
|
V |
||||||
|
|
|
|
||||
dV V |
d |
. |
|||||
|
|
||||||
|
|
|
|
|
|
||
Подставив (11.24) в (11.23), получим |
|||||||
E |
dp |
, и скорость волны – формула (11.20) - примет вид |
|||||
d |
|||||||
|
|
|
|
|
|||
(11.24)
|
dp |
|
d |
||
|
.
(11.25)
Это выражение справедливо для волн в жидкостях и газах.
Опыт показывает, что при распространении звука в газе возникают быстро чередующиеся зоны сжатия и разряжения среды. Эти участки не успевают обмениваться теплом, то есть имеет место термодинамический процесс без теплообмена, и связь между давлением и объемом определяется уравнением адиабаты
pV |
const, где |
(11.26) |
- постоянная адиабаты,
|
C |
p |
|
||
|
|
|
|
C |
|
|
V |
|
, где
C |
p |
|
- теплоемкость газа при постоянном
давлении, а
CV
- при постоянном объеме. Запишем дифференциал натурального
логарифма:
ln V ln |
p ln const |
||||
|
dV |
|
dp |
0 , |
|
V |
p |
||||
|
|
|
|||
откуда
dVdp Vp ,
и формула (11.23) принимает вид
E p
Таким образом, скорость звуковой волны в газе
(11.26)
|
|
p |
|
|
|
|
|
|
|
. |
|
|
|
|
|
(11.27) |
|||
|
|
|
|
|
|
|
|||
Если учесть уравнение состояния идеального газа |
|||||||||
pV m RT , а также |
|
m |
|
p |
, |
то уравнение (11.27) станет таким: |
|||
|
|
||||||||
|
|
|
|
V |
R T |
|
|||
|
RT |
, |
|
|
|
|
|
|
(11.28) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
где R - универсальная газовая постоянная, |
- молярная масса газа. |
||||||||
5 Энергия упругой волны
Прежде всего найдем выражение для плотности упругой (потенциальной) энергии растянутого (или сжатого) стержня на величину x . По закону Гука F (x) kx , где k -
коэффициент упругости. Работа силы F (x) в этом процессе
8

|
x |
|
x |
|
k x |
2 |
|
A |
|
F (x)dx |
|
k xdx |
. |
||
2 |
|||||||
|
|
||||||
|
0 |
|
0 |
|
|
||
|
|
|
|
|
Эта работа идет на увеличение упругой энергии
|
|
k x |
2 |
|
WП |
|
. |
||
2 |
||||
|
|
|
Плотность же упругой энергии
WП
стержня, значит
(11.29)
wП |
|
W |
П |
, |
|
где |
||||
|
|
|
||||||||
S |
l |
|
||||||||
|
|
|
|
|
|
|
|
|||
что |
|
|
|
|
|
|
|
|
|
|
kx F |
S , |
|||||||||
получим |
|
|
|
|
|
|||||
W |
|
|
F x |
|
|
|
||||
П |
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
Отсюда |
|
|
|
|
|
|
|
|||
w |
|
|
E 2 |
|
|
|
||||
П |
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
S |
и |
|
E |
S 2
l
l
- площадь поперечного сечения и длина стержня. Учитывая,
|
и |
x |
, |
|
l |
||||
|
|
|
||
|
E |
|
|
|
|
2 |
|
|
|
|
2 |
S l . |
||
|
|
|
||
(11.30)
При прохождении продольной волны в стержне каждая единица объема обладает как
потенциальной энергией упругой деформации |
wП |
так и кинетической |
энергией wК . |
||||||||||||
Плотность полной энергии |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
E |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
w wП wK |
|
|
|
|
|
|
2 |
|
|
(11.31) |
|||||
|
|
|
|
|
|
2 |
t |
|
|
|
|
|
|
||
Учитывая, что |
E |
2 |
, выражение можно переписать так |
|
|||||||||||
|
|
||||||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
w |
|
|
|
. |
|
|
(11.32) |
||||||||
|
|
t |
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запишем уравнение плоской бегущей волны в виде:
|
|
x |
A cos t |
|
|
|
|
|
тогда |
|
|
|
|
|
t |
A sin |
|
|
|
|
t
,
|
x |
|
|
||
|
,
x
A |
|
sin |
|
t |
|
|
|||
|
|
|
|
|
x |
|
|
||
|
, то есть
|
|
|
|
t |
x |
|
|
|
|
||
Отсюда следует, что в (11.32) |
wП |
||
энергии одинаковы и изменяются синфазно.
|
(11.33) |
wK |
, т.е. плотности кинетической и упругой |
Поэтому мы имеем в результате
w 2w |
|
|
|
K |
|
t |
|
|
|
||
|
|
||
Подставив t
w A2 2 sin
|
2 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
и учитывая, что |
k |
|
, получим |
|
|
|
|
|
|
2 t kx . |
|
|
(11.34) |
|
9

Среднее значение плотности энергии за период равно
|
|
A |
|
|
|
|
|
|
2 |
|
2 |
w |
|
|
2 |
|
|
|
|
|
|
|
|
т.к. |
sin |
2 |
t kx |
|
|
|
|||||
|
|
|
|
|
T |
Плотность энергии
,
1 |
1 |
|
2 |
||
|
||
w |
||
cos 2 t kx |
T |
|
|
|
(11.34) и среднее
(11.35)
1 |
. |
|
2 |
||
|
значение  w
w (11.35) пропорциональны
(11.35) пропорциональны
плотности среды
, квадрату амплитуды |
A |
и квадрату частоты |
Плотность потока энергии
волны.
Энергия доставляется от источника колебаний в различные точки среды самой волной. Следовательно, волна переносит с собой энергию. Потоком энергии называется количество энергии, переносимое волной через определенную поверхность S в единицу времени:
dWdt .
Размерность
|
|
Дж |
|
||
СИ |
|
с |
|
|
(11.36)
Вт .
Поток энергии в разных точках поверхности |
S |
может иметь различную |
интенсивность. Для характеристики этого обстоятельства вводят понятие плотности потока энергии. Эта величина численно равна потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия:
j |
|
|
W |
. |
(11.37) |
|||
S |
|
S |
|
t |
||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
Через площадку S (рис. 6) будет заключенная в объеме цилиндра с основанием
W w V w S t .
перенесена за
S |
и высотой |
время
t :
t
энергия
W
,
Рис. 6
Модуль плотности потока энергии равен
j w
Для определения плотности потока и его направления вводят вектор Умова
|
|
j |
w |
где - вектор скорости волны.
(11.38)
j :
(11.39)
10
