Ряды Фурье

Теорема 1. (О почленном интегрировании ряда Фурье) Пусть функ- ция f непрерывна на и удовлетворяет условию f(-π) = f(π), а - её ряд Фурье. Тогда при всяком справед- ливо равенство

причем ряд сходится равномерно на .

► Рассмотрим интеграл с переменным верхним пределом:

. Эта функция непрерывна на , причем , так как

=

= Функция F имеет на . непрерывную призводную: , причём, очевидно, . В силу теоремы 3 F разлагается на в равномерно сходящийся ряд Фурье:

.

Найдем коэффициенты этого ряда. При натуральных k , интегрируя по частям, получим:

=

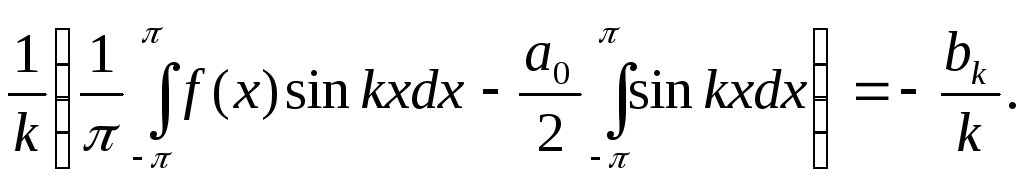= - Аналогично: Таким образом, при всяком х

. Положим здесь х =0 :

0 = . Отсюда: Значит,

Отсюда: ◄

п.5. Ряды Фурье в случае произвольного промежутка

Пусть [a,b], a<b, - некоторый сегмент. Функция , где , возрастает на [a,b] и отображает этот сегмент на . Об- ратная функция возрастает на от a до b.

Пусть функция f (х) абсолютно интегрируема на [a,b]. Тогда функция определена на и абсолютно интегрируема на нем. Пусть ряд Фурье функции φ сходится на , а σ(t) – его сумма:

σ(t) = . Обозначим: S(x) = σ(). Функция S(x) есть сумма тригонометри- ческого ряда, сходящегнося на [a,b]:

S(x) = . Выразим коэфициенты и через функцию f :

;

при всяком натуральном k

;

.

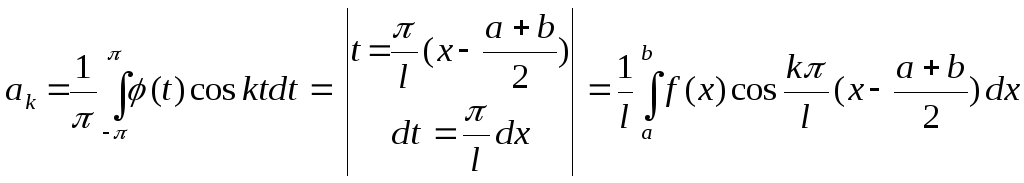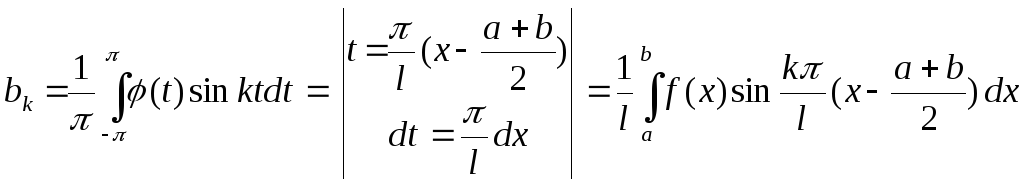Теоремы 1,2, и 3, п.3, описывают поведение суммы ряда Фурье σ(t) в зависимости от свойств функции . Используя замену , не- трудно получить из этих теорем аналогичные утверждения, описывающие поведение суммы S(x) в зависимости от свойств функции f (х). Например, из теоремы Дирихле следует: пусть функция f (х) кусочно- монотонна и кусочно- непрерывна на сегменте [a,b]; тогда

1) для всякого х(a,b) S(x) =

2)

Замечание. Во всякой точке интервала (a,b), в которой f непрерыв- на, имеет место равенство f(х) = S(x).

Отметим особо случай, когда сегмент [a,b] симметричен относи - тельно нуля: Замена отображает [-l,l] на , обратная замена имеет вид Тогда тригонометрический ряд, построенный описанным выше способом для функции f(х), абсолютно интегрируемой на [-l,l], будет выглядеть так: , где , а при всяком натуральном k , .

Заметим ещё, что если f – чётная функция, то , а , так что тригонометрический ряд содержит только косинусы: . Если же f – нечётная функция,то а = , а , и ряд содержит только синусы: .

п.6. Ряд Фурье функции с интегрируемым квадратом

Пусть функция f определена во всех точках сегмента , за исключением, быть может, точек x_j, j=0,1,2,…,l, и удовлетворяет требованию: интеграл существует. Такую функ- цию f будем называть функцией с интегрируемым на квадратом. Заметим, что функция с интегрируемым на квадратом, абсолютно интегрируема на . Действительно, из очевидного неравенства следует: , где , причем существует; по признаку Вейерштрасса f абсолютно интегрируема на . Полеэно ещё заметить, что не всякая абсолютно интегрируемая функция имеет интегрируемый квадрат. Например, : интеграл сходится, а - расходится.

Теорема 1. (Минимальное свойство коэффициентов Фурье)

Пусть f – функция с интегрируемым на квадратом, а

- я частичная сумма ряда Фурье этой функции. Тогда для всякого тригонометрического многочлена порядка не выше n справедливо неравенство

.

► Рассмотрим , где T_n (x). Имеем: = -2 + .

= =

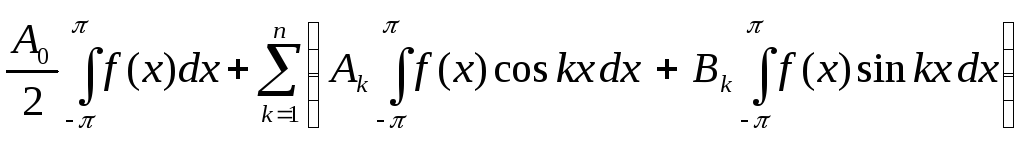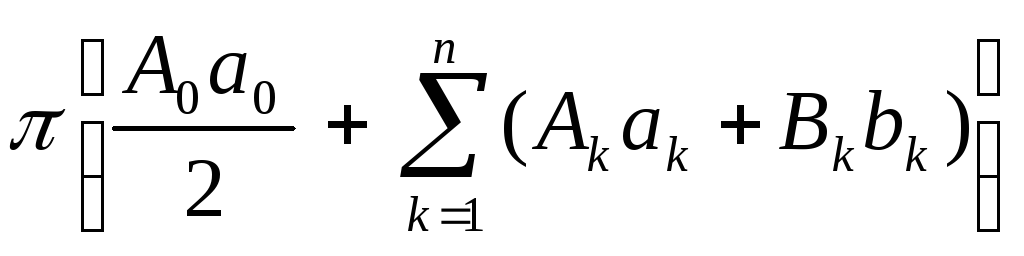= + = . Вычисляя , учитываем равенства леммы п.2:

= .

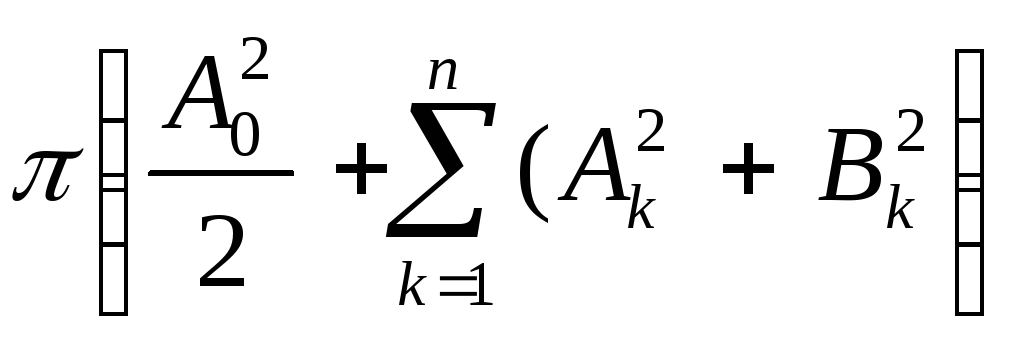Теперь получим:

= - 2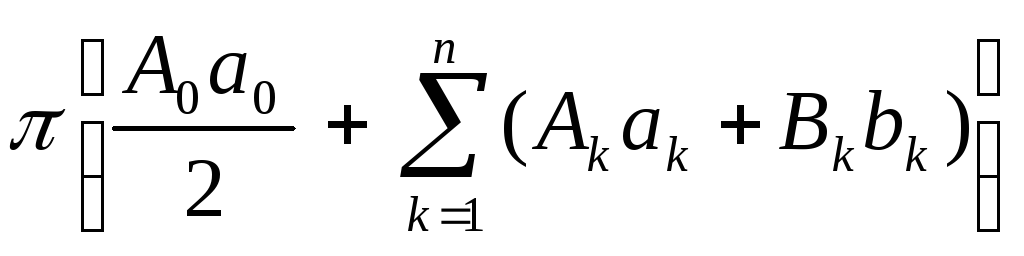 + +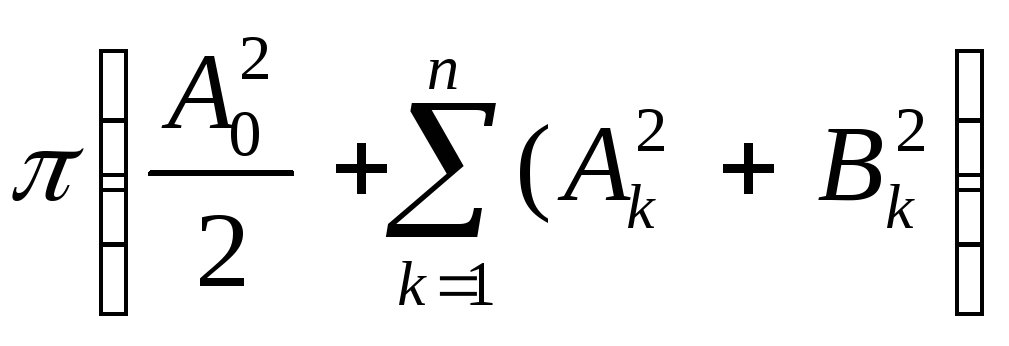= +. Каждую из разностей дополним до полного квадрата:

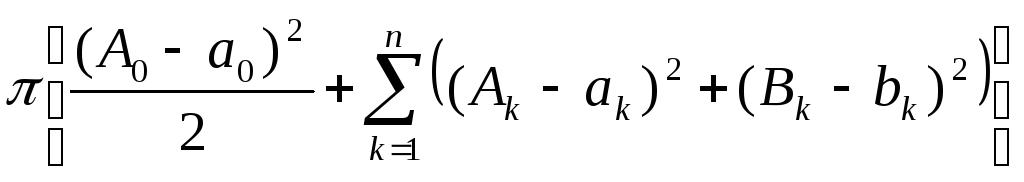= + - . От коэффициентов многочлена зависит только выражение в квадрат- ных скобках; это выражение неотрицательно и обращается в нуль, когда коэффициенты многочлена совпадают с соответствующими коэффициен- тами Фурье функции f : , т.е. в случае =. Значит, =. ◄

Следствие. Если f – функция с интегрируемым на квадратом, то ряд сходится, причем справедливо неравенство (неравенство Бесселя) .

► При всяком натуральном n имеем:

=. Отсюда: всяком натуральном n . Перейдя здесь к пределу при , докажем и сходимость ряда , и неравенство Бесселя. ◄

На самом деле для всякой функции f, квадрат которой интегрируем на , справедливо равенство Парсеваля или уравнение замкнутости:

.

Приведем доказательство этого равенства для функции, непрерыв- ной на .

► Зададим . Так как f непрерывна на , по теореме Вей- ерштрасса (см. п.2) существует последовательность тригономет- рических многочленов , равномерно сходящаяся на к f . Найдется натуральное число такое, что для многочлена из указанной после- довательности на справедливо. Для этого же многочлена имеем (см. доказательство теоремы):

.

Таким образом, . Ввиду произ- вольности отсюда вытекает равенство Парсеваля. ◄

15