Двухшарнирные арки с затяжкой

За основную систему может быть принята криволинейная балка с перерезанной затяжкой(рис. 2,б). Взаимное смещение сечений разреза затяжки для основной системы равно нулю, поэтому каноническое уравнение метода сил имеет вид:

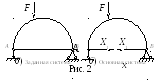
(12)

где δ₁₁ – взаимное смещение сечений разреза по направлению силыХ₁от действия силыХ₁= 1; Δ_1F – то же, от внешней нагрузки.

Выражение для Δ_1Fбу-дет то же, что и для аналогичной двухшарнирной арки (7) или (11). Для перемещенияδ₁₁добавляется влияние удлинения затяжки длинойl в состоянииХ₁= 1:

,

где Е_зА_з– жесткость затяжки на растяжение. Следовательно, будем иметь

(13)

и тогда (14)

Распор в двухшарнирной арке с затяжкой будет всегда меньше, чем распор в двухшарнирной арке, так как знаменатель формулы (14) всегда будет больше знаменателя формулы (2).

Бесшарнирные арки

Бесшарнирная арка – трижды статически неопределима (рис. 3, а). Рассмотрим расчет симметричной арки. За основную систему можно принять любую из показанных на рис. 3,б, в, г. Как будет установлено в дальнейшем, основная система, изображенная на рис. 3,г, является лучшей. В этой системе используется невесомые и абсолютно жесткие консоли длинойс. Так как из условия равновесияХ₁=Н, то неизвестноеХ₁называют распором.

Система канонических уравнений метода сил примет вид:

(15)

Моменты ив произвольном сечении арки можно представить в виде:

(рис. 3, д, е).

Подберем длину консоли стак, чтобыδ₁₂было равно нулю, то есть

где s– вся дина арки. Принимая во внимание симметрию арки, запишем

откуда определяем длину жесткой консоли:

(16)

Таким образом, принимая длину жесткой консоли спо формуле (16), мы будем получатьδ₁₂=δ₂₁=0 и тогда система уравнений (15) еще более упростится и примет вид:

(17)

Влиянием иN_F, Q_F пренебрегаем. Тогда

(18)

(19)

Подставляя выражения (18), (19), определяемые точным или приближенным интегрированием, в канонические уравнения (17), находим лишние неизвестные Х₁,Х₂иХ₃. Затем переходим к вычислению усилий в произвольном сечении арки и построению соответствующих эпюр.

Пример.Рассчитать бесшарнирную круговую арку постоянного поперечного се-чения на гидростатическую нагрузку (рис. 4,а).

Согласно рис. 4, аи рис. 4,вимеем:dy=dssinφ;

dx = dscosφ; x = rsinφ;

y = r – rcosφ; ds = rdφ;

sinα = l/(2r); cosα = (r – f) / r;

q_x = qdssinφ = qdy;

q_y = qdscosφ = qdx.

По формуле (16) находим

.

Формулы (18) дают:

Подставляя полученные параметры в формулы (18), (19), находим необходимые коэффициенты, например,

А затем из формул (17) определяем неизвестные Х₁,Х₂ иХ₃= 0.

Л е к ц и я 15

Неразрезные балки

Неразрезной балкойназывается брус, который перекрывает два или более пролетов (рис. 1).

Число лишних неизвестных подсчитывается по формуле:

Л = –W = C_o – 3D = C_o – 3. (1)

В качестве основной системы выберем совокупность однопролетных шарнирно опертых балок с неизвестными опорными моментами.

Запишем систему канонических уравнений:

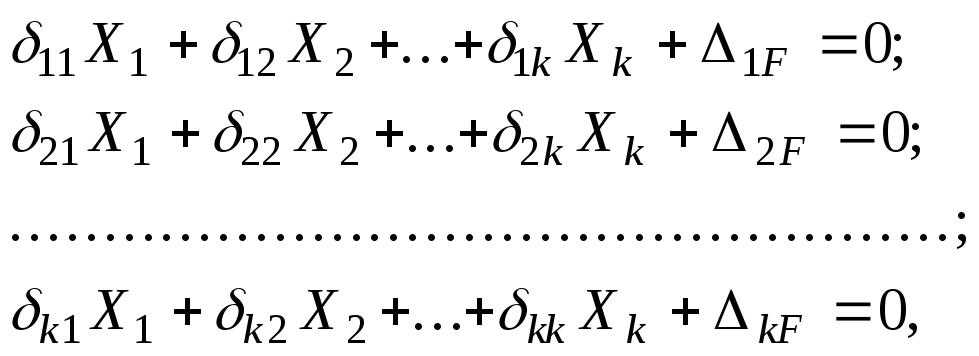(2)

где k– общее число отброшенных связей.

Из рассмотрения единичных эпюр следует, что в каждое из канонических уравнений (2) будет входить по три неизвестных, только в первое и последнее – по два неизвестных:

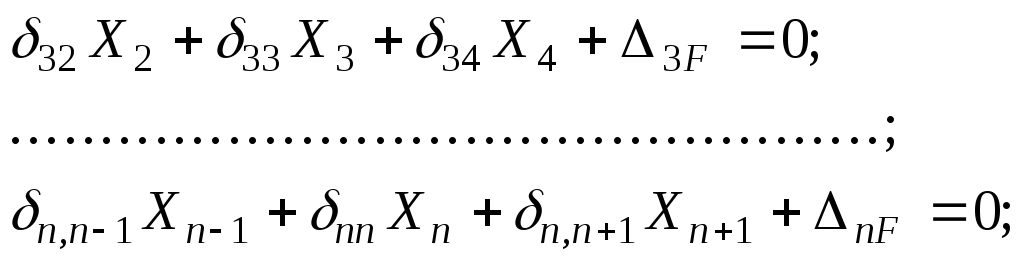
(3)

Перемещения δ_ijбудем подсчитывать по формуле:

(4)

то есть, пользуясь правилом Верещагина, получим

(5)

где Ω_nиΩ_n+1– площади эпюр моментов вn–й и (n + 1)–й однопролетных балках от внешней нагрузки. аa_nиb_n+1– расстояния от центров тяжести этих эпюр до (n– 1)- й и (n+ 1)-й опор соответственно. Параметрпредставляют собой правую фиктивную опорную реакцию вn–м пролете при загружении его распределенной нагрузкой в виде эпюры моментов вn–й однопролетной балке, а– левая фиктивная опорная реакция в (n+1)-м пролете при загрузке его распределенной нагрузкой в виде эпюры моментов этой однопролетной балки.

Подставляя значения коэффициентов (5) в канонические уравнения (3), запишем

(6)

Чтобы подчеркнуть, что за неизвестные Х_i приняты опорные моментыМ_i, в дальнейшем будем вместоХ_iписатьМ_i. Кроме того, умножим уравнение (6) на 6ЕI, тогда

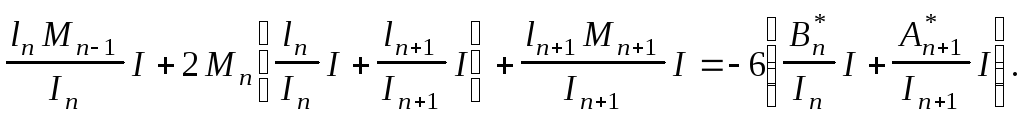
Окончательно запишем:

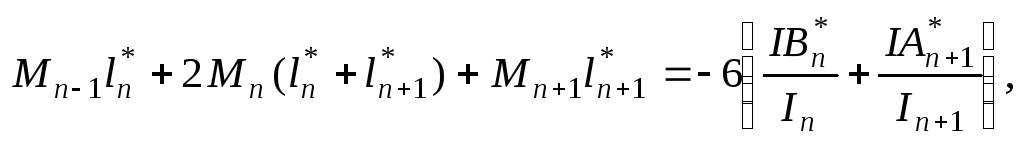(7)

где и- приведенные пролеты,

I– момент инерции поперечного сечения любого пролета.

Уравнение трех моментов(7) илиуравнение Клайперонабыло выведено в 1857 году. Если моменты инерции в пролетах – постоянные, то уравнение (7) принимает вид:

(8)

После определения неизвестных опорных моментов строят эпюры изгибающих моментов и поперечных сил, используя формулы

(9)

Прогибы в неразрезной балке n–го пролета определяют как в однопролетной балке при наличии опорных моментовМ_n–1,М_nи заданной пролетной нагрузки.

Пример 1(рис. 3). Построить эпюры изгибающих моментов и поперечных сил для трехпролетной неразрезной балки постоянного поперечного сечения.

Запишем уравнения трех моментов (8) для рассматриваемой балки:

n= 1:

n= 2:

Учитывая, что М₀=М₃= 0, а также, чтозапишем два вышеприведенных уравнения как

где Окончательно имеем:

Решая полученные два уравнения, находим:

Затем определяем поперечные силы по каждому участку:

Пример 2.Построить эпюры изгибающих моментов и поперечных сил для однопролетной балки, показанной на рис. 4.

Запишем уравнение трех моментов (8) при n= 1:

или где

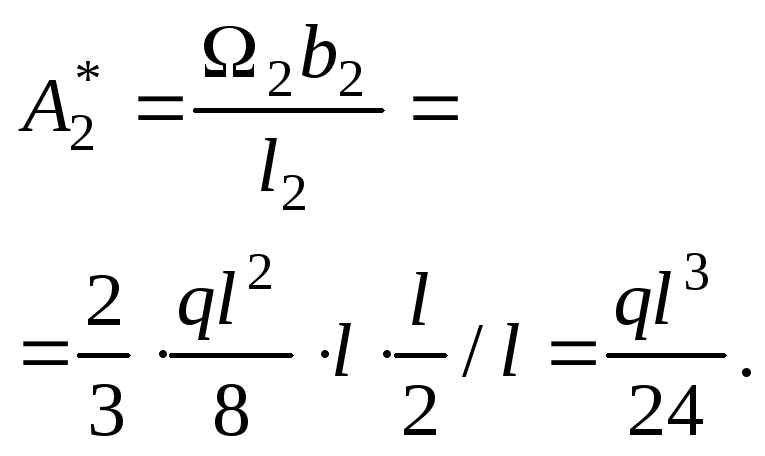
Затем находим

и строим эпюры MиQ(рис. 4).

Л е к ц и я 16