Binder1

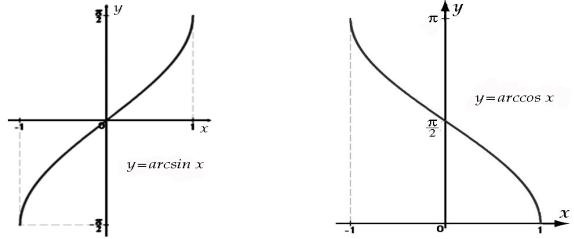
Последние два соотношения позволяют истолковать arcsin т, где -1 т 1,

так: arcsin т – это число взятое в пределах от 2 до 2 и такое, что его синус

равен т.

График функции у=arcsin x изображен на рисунке 29.

получим cos (arccos x) = х. Следовательно для любого х из [-1; 1] имеем: cos (arccos x) = х, 0 arccos x .

Последние два соотношения позволяют истолковать arccos т, где -1 т 1, так: arccos т – это число, взятое в пределах от 0 до и такое, что его косинус равен т.

Отметим, что имеет место следующее тождество: arccos x arccos x .

В его справедливости можно убедиться с помощью графика функции у=arccos x, изображенного на рисунке 30.

45

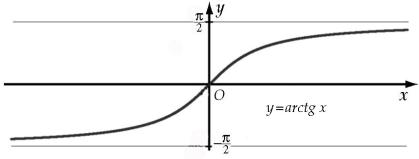
Функция у=arctg x является обратной к функции y=tg x.

1)Область определения – множество всех действительных чисел.

2)Область значений – интервал ; .

2 2

3)Функция нечётная: arctg x arctgx .

4)Функция возрастающая.

что его тангенс равен т.

График функции у=arctg x изображен на рисунке 31.

Рис. 31

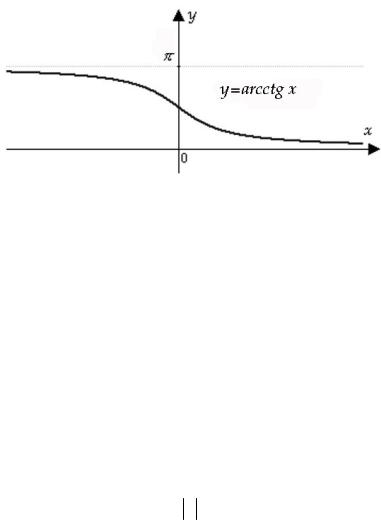
Функция у=arcctg x является обратной к функции y=ctg x.

1)Область определения – множество всех действительных чисел.

2)Область значений – отрезок (0; ).

3)Функция не является ни чётной, ни нечётной.

4)Функция убывающая.

Из сказанного выше следует, что записи у=arcctg x и х = ctg у , 0 < y < , эквивалентны. Для любого x имеем:

ctg (arcctg x) = х , 0 < arcctg x < .

46

Последние соотношения позволяют истолковать arcctg т, так: arcctg т – это число, взятое в пределах от 0 до (исключая сами значения 0 и ) и такое, что его котангенс равен т.

Имеет место тождество: arcctg(-x) = - arcctg x.

График функции у=arcctg x изображен на рисунке 32.

Рис. 32

Преобразование графиков. Пусть известен график функции y f x . Зная

влево, если а < 0.

2. График функции у = f(x)+b получается из исходного графика путем параллельного переноса вдоль оси OY на b единиц вверх, если b > 0, или вниз, если b < 0.

3. График функции у = f(Аx), если А > 0, А 1, получается из исходного графика путем сжатия в А раз вдоль оси 0X , если А>1, или растяжения в 1/А раз вдоль оси OX , если 0<A<1.

Сжатие вдоль оси 0X – это уменьшение абсцисс точек исходного графика без изменения ординат. Растяжение вдоль оси 0X – это увеличение абсцисс точек исходного графика без изменений ординат.

47

4.График функции у = Вf(x), если В > 0, В 1 получается из исходного графика путем сжатия в 1/В раз вдоль оси OY , если 0<В<1, или растяжения в В раз вдоль оси OY , если В>1.

Сжатие вдоль оси OY – это уменьшение ординат точек исходного графика без изменения абсцисс. Растяжение вдоль оси OY – это увеличение ординат точек исходного графика без изменения абсцисс.

5.График функции у=f(-x) получается из исходного путем симметричного отображения относительно оси OY .

6.График функции у=-f(x) получается из исходного путем симметричного отображения относительно оси OX .

Покажем, как применяя эти преобразования, можно построить график

Тогда получим: у b1 x Aa1 .

Согласно правилам преобразования графиков, график функции может быть построен с помощью следующих действий:

1.Построим график функции y 1x .

2. График y Ax получим, сжимая (растягивая) вдоль оси OY гиперболу y 1x , если A 0 , то еще и симметрично отображая относительно оси OX .

48

3.А затем сделаем параллельный перенос предыдущего графика вдоль оси ОХ

предыдущего графика вдоль оси 0Y на b1 единиц вверх или вниз.

Таким образом, графиком дробно-линейной функции является гипербола, центр которой находится в точке О1 (а1, b1) .

Взаключение этого обзора рассмотрим еще две функции:

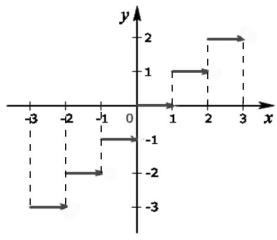
1.Функция y = [x] – целая часть числа. Если 0 х < 1, то у = [x] = 0; если 1 х < 2, то у = [x] = 1; если -1 х < 0, то у = [x] = -1 и т.д. График функции y = [x] изображен на рисунке 33.

Рис. 33.

2.Функция y = {x} – дробная часть числа, т.е. x x x . Построим график функции y = {x}. Заметим, что {x+1} = {x}, поэтому достаточно построить ветвь на любом промежутке длиной 1, например на [0; 1). Если

0 x <1, то [x] =0, а потому {x} = х.

На рисунке 34 изображен график функции y = {x} на промежутке [0; 1) и на всей числовой оси.

49

Рис. 34

Примеры решения задач

доказать.

Пример 3. Доказать, что функция f x sinx3 x является четной функцией.

Решение. Условие четности функции f x f x . Найдем

Пример 4. Найти область определения функций:

50

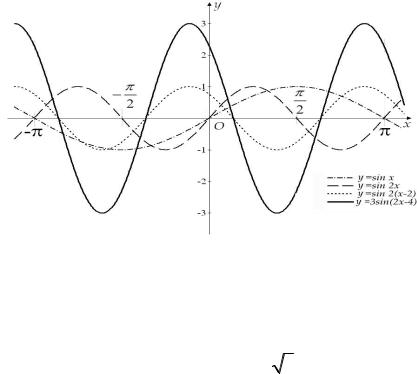
Пример 6. Построить график функции y 3sin 2x 4 .

Решение. Заданную функцию представим в виде y 3sin 2 x 2 и строим график в следующем порядке:

1)На отрезке 0; 2 строим y sin x.

2)Сжимая в 2 раза вдоль оси OX строим y sin 2x

3) График функции y sin 2 x 2 получим путем параллельного переноса графика функции y sin 2x вправо вдоль оси OX на 2 единицы масштаба.

4) Увеличивая ординаты точек графика функции y sin 2 x 2 в три раза, не изменяя абсцисс этих точек получим график функции

y 3sin 2x 4 . (См. рис. 36)

52