
Решение нелинейных уравнений_МУ и варианты
.pdf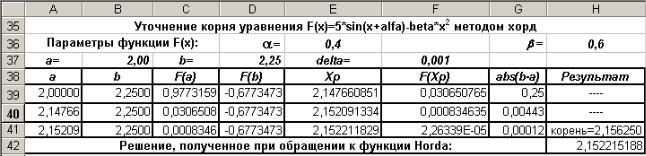
Ниже приводится текст функции VBA, реализующей алгоритм метода хорд.
Public Function Horda(a As Double, b As Double, delta As Double) As Double Dim С As Double, Fa As Double, Fb As Double, Fс As Double, L As Boolean Fa = F(a) ' --- вычисление значения исследуемой функции
Fb = F(b) '--- вычисление значения исследуемой функции
If Fa * Fb > 0 Then
MsgBox ("Интервал [a, b] выбран неправильно")
Exit Function
End If Do
С = a - (b - a) / (Fb - Fa) * Fa
Fс = F (С) '--- вычисление значения исследуемой функции
If Fс * Fa > 0 Then b = С: Fb = Fс Else a = С: Fa = Fс If (Abs(b - a) < delta) and (Abs(Fс) > delta*100) Then _
MsgBox (" Точка С=" & C & " возможно является точкой разрыва") : Exit Function L = (Abs(b - a) < delta) Or (Abs(Fс) < delta)
Loop Until L Horda = С
End Function
Рис. 12. Результаты применения метода хорд для уточнения корня функции
F(x)=5*sin(x+ )- *x2
Метод простых итераций
Витерационных методах, которые иначе называют методами последовательных приближений, многократно повторяется - "итерируется" (от латинского "итерацио" - повторение) некоторый единообразный вычислительный процесс. В результате каждой итерации получаются всё более точные приближения к искомому решению.
Вобщем виде итерационная формула определяется приведением уравнения
(1) к равносильной форме
Х=φ(X). |
(8) |
|
После записи уравнения (1) в виде (8) определяется начальное значение Х0 - "нулевое приближение". Последующие приближения вычисляются по формулам Х1=φ(X0), Х2=φ(X1),…, или в общем виде
Хi+1 =φ(Xi ). |
(9) |
Возможны два варианта поведения итерационного процесса.
11
В первом случае итерационный процесс сходится, последовательные приближения Хi стремятся к некоторому конечному пределу, который и является решением уравнения (1). Во втором варианте процесс расходится, конечного предела приближений не существует. Из расходимости процесса не следует, что решения уравнения (1) не существует, а следует только то, что способ построения итерационного процесса выбран неудачно.
Покажем это на простом примере. Сравним две формы равносильной записи уравнения
X |
X |
1 |
(10) |
||
|
|||||
2 |
|
|
|
|
|
и |
|
||||
X = 2X - 2 |
|
|
(11) |
||
Эти уравнения имеют очевидное решение X 2. |
Определим начальное |
||||
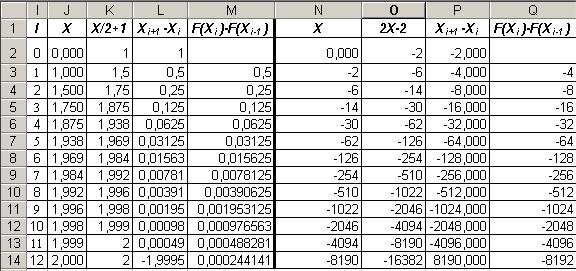
значение Х0 =0 и вычислим последовательные значения Хi для итерационных процессов, определяемых формулами (10) и (11). Результаты итерационных вычислений по формулам (10) и (11) приведены на рис. 14.
Рис. 14. Сравнительная таблица итерационных процессов для двух представлений равносильных уравнений (10) и (11)
Процесс, определяемый уравнением (10) сходится, а процесс (11) - расходится.
В первом случае значения аргумента Х изменяются быстрее, чем значения функции F(X) (сравниваем значения Xi+1-Xi и F(Xi+1)-F(Xi) в левой части таблицы рис. 14). Скорость изменения функции определяется значением её производной. Сходимость итераций, определяемых процессом (9), обеспечивается в тех случаях, когда значения функции φ(X) изменяются медленнее, чем значения аргумента Х. Дифференцируя уравнение (8), определим условие сходимости процесса итераций
| φ'(X) | < | Х' | = 1. |
(12) |
12

Метод Ньютона (метод касательных)
Итерационный процесс в методе Ньютона определяется исходя из формулы разложения функции F(x) в ряд Тейлора
F(X 0 |
h) F(X 0 ) |
h |
F'(X |
0 ) |
h2 |
F"(X 0 ) ... |
(13) |
|
|
||||||
|
1! |
2! |
|
|
|||
Учитывая в этой формуле первые два члена и, функции F(x) в точке X0+h равно 0, получим
F(X0)+hF'(X0)≈0
Из (14) получим значение h:
h F ( X 0 )
F '( X 0 )
предполагая, что значение
(14)
(15)
и далее, положив X1=X0+h, получим итерационную формулу метода Ньютона
X1 |
X 0 |
|
F ( X |
0 ) |
(16) |
||
F '( X |
0 ) |
||||||
|
|
|
|
||||
Рассмотрим графическую иллюстрацию алгоритма метода Ньютона.
Рис. 15. Диаграмма алгоритма метода Ньютона
В методе Ньютона нахождение корня уравнения (1) начинается с выбора точки "нулевого приближения" Х0. Этот выбор обычно осуществляется на основании анализа грубого графика исследуемого процесса.
Отбрасывая в формуле Тейлора члены второго и более высоких порядков, мы фактически заменяем график функции F(X) касательной к нему в точке X0. Проделав аналогичные преобразования с функцией в точке X1, получим значение X2. И далее значение X3 и т.д. Цикл итераций
Xi 1 |
Xi |
|
F ( Xi 1 ) |
(17) |
|
F '( Xi 1 ) |
|||||
|
|||||
|
|
|
|
продолжается до тех пор, пока не будет выполнено условие |
|
| Xi - Xi-1 | < δ. |
(18) |
13
Достаточные условия сходимости итеративного процесса, задаваемого формулой (17), к корню уравнения (1) определяются следующей теоремой
[6]:
Пусть F(X) определена и дважды дифференцируема на интервале [a, b], причём F(a)F(b)<0, а производные F '(x),F"(x) сохраняют знак на отрезке [a, b]. Тогда, исходя из начального приближения х0 выбранного в пределах интервала [a, b] и удовлетворяющего неравенству F(х0)F"(х0) >0, можно построить итеративную последовательность (12) для i=0, 1, 2,…, сходящуюся к единственному на [a, b] решению ξ уравнения F(x)=0.
Метод Ньютона эффективен, если известно хорошее начальное приближение и в окрестности корня график функции F(X) имеет большую крутизну.
Как показано при выводе формулы (17) в методе Ньютона уравнение (1) заменяется равносильной формой [6]
|
|
|
|
|
|
X X |
F ( X ) |
X ( X ) |
|
(19) |
|||
|
|
|
|
|
|
|
|
или |
|
||||
|
|
|
|
|
|
F '( X ) |
|
|
|||||
Производная правой части уравнения (19) |
|
|
|
|
|||||||||
|
F ( X ) |
' |
|
|
F '( X )F '( X ) F ( X )F"( X ) |
|
F ( X )F"( X ) |
|
|||||
X |
|
|
|
1 |
|
|
|
|
|
|
|
|
(20) |
|
|
|
|
2 |
|
|
2 |
||||||
|
|
|
|
|
|
F '( X ) |
|
|
F '( X ) |
||||
|
F '( X ) |
|
|
|
|
|
|
|
|
||||
Условие сходимости итерационного процесса при выборе начальной точки х0 определяется соотношением
F(x0 ) F"(x0 ) |
1 |
(21) |
||
F'(x |
0 )2 |
|
||
|
|
|
||
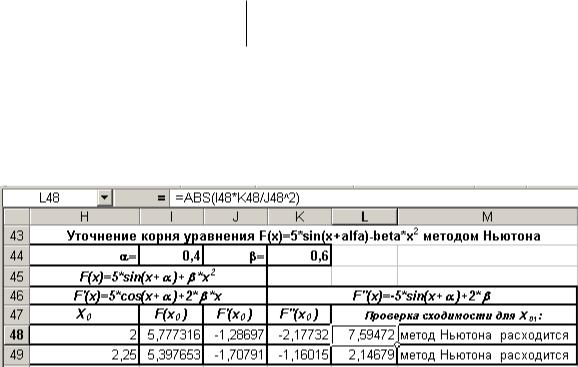
Для проверки условия сходимости метода Ньютона в рассмотренном нами примере, определим её первую и вторую производные функцию F(x)=5*sin(x+ )- *x2 и. Проверка условия сходимости итерационного процесса метода Ньютона, выполняемая по формуле (21) показывает, что для выделенного интервала [2,00; 2,25] метод Ньютона неприменим.
Рис. 16. Проверка возможности применения метода Ньютона для уточнения значения
корня функции F(x)=5 sin(x+ )- x2 при выборе начальной точки на границах интервала [2,00; 2,25]
14
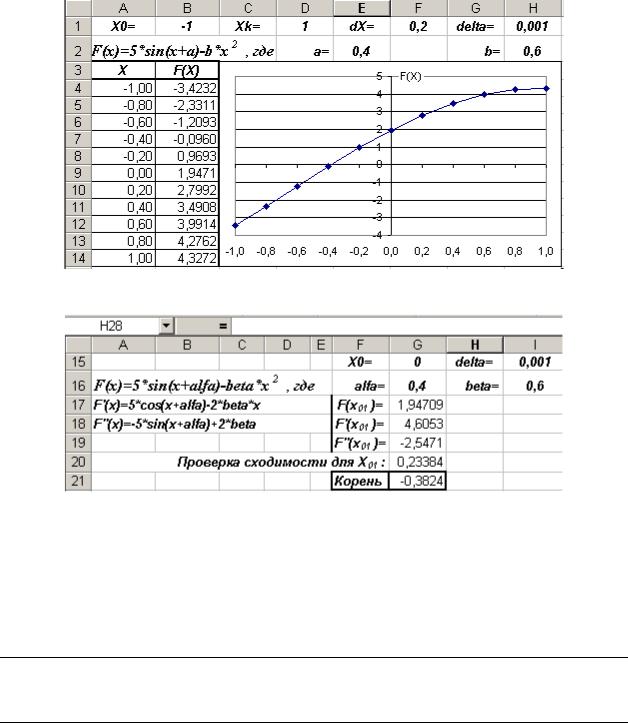
Изменим интервал изменения аргумента х для функции F(x)=5 sin(x+ )- x2. Анализ этого уравнения в диапазоне изменения аргумента Х [-1,0; 1,0] позволяет выделить ещё один подынтервал с одним корнем.
На рис. 17 приведена таблица и диаграмма с результатами выделения корня, выполненного для подынтервала изменения аргумента Х [-1,0; 1,0].
В этом подынтервале находится один корень. Применение метода Ньютона для уточнения корня, находящегося в этом интервале, позволяет получить значение корня равное
Рис. 17 Таблица и диаграмма с результатами выделения корня при изменении аргумента Х в диапазоне [-1,0; 1,0].
Рис. 17. Нахождение корня методом Ньютона
VBA реализация метода Ньютона
1. Запишем функции, реализующие вычисления значений F(x), F'(x) и F"(x).
Public Function Fsin(alfa As Double, beta As Double, x As Double) As Double Fsin = 5 * Sin(x + alfa) - beta * x ^ 2
End Function
Public Function Fsin1(alfa As Double, beta As Double, x As Double) As Double Fsin1 = 5 * Cos(x + alfa) - 2 * beta * x
End Function
Public Function Fsin2(alfa As Double, beta As Double, x As Double) As Double Fsin = -5 * Sin(x + alfa) - beta
End Function
15
2.Блок-схема алгоритма метода Ньютона приведена на рис. 18.
3.Текст функции, реализующей алгоритм метода Ньютона:
Public Function Njuton(X0 As Double, delta As Double, alfa As Double, beta As Double) As Double
Dim FX As Double, F1 As Double, F2 As Double, X1 As Double, dx As Double FX = Fsin(alfa, beta, X0)
F1 = Fsin1(alfa, beta, X0)
F2 = Fsin2(alfa, beta, X0)
If (Abs(FX * F2 / F1 ^ 2) > 1) Then
MsgBox ("X0 выбрана неправильно. Процесс расходится")
Exit Function End If
Do
X1 = X0 - Fsin(alfa, beta, X0) / Fsin1(alfa, beta, X0) dx = Abs(X1 - X0)
X0 = X1
Loop Until dx < delta Njuton = X1
End Function
нет
7
X0=X1
FX=F(X0),
Function Njuton(X0,δ)
1 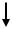
Ввод
параметров
X0,δ
2
FX=F(X0), F1=F'(X0)
F2=F"(X0)
4
3 да Процесс
|FX*F2/F12|>=1?  расходится
расходится
нет
|
5 |
|
|
|
|
|
|
|
|
|
FX |
|
|
||
|
|
|
|
|
Exit |
||
X1 X0 |
|
|
|||||
|
|
|
|||||
F1( X0 ) |
|
|
|||||
|
|
||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
6
|X1-X0|>
да
8
Njuton = X1
конец
16
Рис. 18. Блок-схема алгоритма метода Ньютона
Варианты заданий к лабораторной работе "Решение нелинейных уравнений"
С точностью ε = 0,5•10-3 вычислить наименьшие по модулю корни уравнений.
|
|
Варианты заданий |
|
№ |
Уравнение 1 |
Уравнение 2 |
|
вар. |
|||
|
|
||
1 |
Х3 + 1,3Х2 – 4,7 = 0 |
(Х – 1)2 = 0,5еХ |
|
2 |
Х3 + 13,4Х2 – 3,2 = 0 |
Ln(X)+ X = 0 |
|
3 |
Ln(X)- X-2=0 |
X – cos(X/2) = 0 |
|
4 |
Х3 + 0,86Х – 3,8 = 0 |
2 Ln(X)+ X = 0 |
|
5 |
Х3 + 3,1 Х – 9,4 = 0 |
e-Х = 2- X2 |
|
6 |
ctg(X) - Х2 = 0 |
2 Ln(X) – 0,5 X + 1 = 0 |
|
7 |
1,8 Х2 – sin(10 X) =0 |
e-Х –(X – 1)2 = 0 |
|
8 |
Х3 - 2 Х – 5,2 = 0 |
tg(X) = 1 / (5X) |
|
9 |
Х3 - Х + 1 = 0 |
X Lg(X) = 4,78 |
|
10 |
Х3 + 2,8 Х – 8,3 = 0 |
(7 - X2) = X2 / 3 +1 |
|
11 |
Х3 + 5,8 Х – 23 = 0 |
2 – X = Lg(X) |
|
12 |
Х3 + 2,7 Х – 9,4 = 0 |
eХ/3 = 6 – 0,5 X2 |
|
13 |
Х3 + 0,72 Х – 6,5 = 0 |
4 X – 7 sin(X) = 0 |
|
14 |
Х3 + 0,59 Х2 – 8,1 = 0 |
tg(X) = X |
|
15 |
Х3 + 0,92 Х – 4,6 = 0 |
X Ln(X) = 14 |
|
16 |
Х3 - 2,7 Х – 9,4 = 0 |
sin(X) = 0,8 X |
|
17 |
Х3 + 3 Х + 1 = 0 |
tg(X) =2 / X |
|
18 |
Х3 + 0,86 Х – 3,8 = 0 |
3 sin(X/2) = 2 X2 |
|
19 |
Х3 - Х + 1 = 0 |
X Lg(X) = 4,78 |
|
20 |
Х3 + 2,6 Х – 6,3 = 0 |
(7 - X2) = X2 / 3 +1 |
Список рекомендуемой литературы
1.Конспект лекций.
2.Заварыкин В.М. и др. Численные методы: учеб. пособие для студентов. – М.: Просвещение, 1990.
3.Цыпкин А.Г., Цыпкин Г.Г. Математические формулы: Справочник. – М.: Наука, ГФМЛ, 1985.
4.Фрид Э. и др. Малая математическая энциклопедия. – Изд-во АН Венгрии, Будапешт, 1976.
17
5.Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. - Томск: МП "РАСКО", 1991.
6.Зельдович Я.Б., Мышкис А.Д. Элементы прикладной математики. - М. Наука ГФМЛ, 1967
18
