Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математический анализ в примерах и задачах

.pdf

Скачиваний:

637

Добавлен:

27.03.2015

Размер:

2.2 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1819 / 2119 20 21 > Следующая >>>

7.6. Приближенные методы вычисления…								121
Способ Симпсона.			Отрезок		разделен на		8 частей.	Значит,
2n 8,	n 4. Вычислим множитель перед						скобкой в	формуле
Симпсона:
		b a		1 0	1	0,041667.
		6n			24	0,041667.
		6n		6 4	24

Тогда:

1 y0 y8 1,00000 2,71828 3,71828. 2 y1 y3 y5 y7

1,13315 1,45499 1,86824 2,39888 6,39888. 4 2 27,42104.

3 y2 y4 y6 1,28402 1,64872 2,11700 5,04974. 2 3 10,09948.

В итоге:

I 0,041667( 1 4 2 2 3) 0,041667(3,71828 27,42104 10,09948),

I 0,041667 41,23880 1,71829.

После запятой здесь верны четыре знака, в то время как формула трапеций давала только один верный знак. Погрешность по сравнению с точным значением составила R 1,71829 1,71828 0,00001,

что следует признать хорошей точностью.

Задачи для самостоятельного решения

Вычислить приближенно следующие интегралы с помощью: а) формулы трапеций (It ), б) формулы Симпсона (Is ).

0,8

95. sin xdx,

n 10.

96.

n 10.

97. cosxdx,

n 10.

arctg

98. exdx,

n 8. 99.

dx, n 10.

100. e x2dx,

n 10.

101. lg xdx ,

102.

n 10.

dx,

n 6.

1 x2

122				Г л а в а 7. Определенный интеграл
ОТВЕТЫ К ЗАДАЧАМ ГЛАВЫ 7
1.(b a).	2. v0t gt2 /2.		3. 3. 4. 210 1 /ln2.		5. ln b/a .
6. (b2 a2)/2. 7.		cosa cosb.		8. /2. 9. «+».	10. «+».	11. «–».
12. «+».	13. «–».	14. «–».	15. «1». 1 6. «2».		17. «1».	18. «1».
19. 1/3.	20. 1/2.	21. 20/9.	22. 2ln 6/5 0,365. 23. 2 I					.
							5

24.	2	I			2	.	25.	1	I	2		.
	9
				7			2			2
			1							9
29.				. 30.			2 .		31. ln		.
	8		4							8

26. 2 I 2 . 27. 7 . 28. 16 .

13		7	3		3
32. arctge	.		33.	.	34. 1 cos1.

4			4

																2												/2				dt								ln3
35.				.					36.				2														37.	/6						.			38. dt .
																2						tdt .

	2																													1 sin2 t
	2															1														1 sin2 t										ln2
				f (arctgt)																																	2				1
39.				f (arctgt)									dt .						40. 4 2ln3.									41. 2 /2.					42.				2			arctg	1						.
								1 t2
								1 t2																														5						5
	0
	8						3				.
43.							3			3								44. 7 2ln2.										45. 32/3.						46. 3 /16 .
43.									2									44. 7 2ln2.										45. 32/3.						46. 3 /16 .
									2																				50. 0,5 e 1 .													2
47.						/3.									48. /2 1.												49. 1.												51. 1						.
			3
			3
		1																							1																	e
52.					.						53.															ln2.			54. a2 /4.										55. 6 2e.
52.					.						53.								3							ln2.			54. a2 /4.										55. 6 2e.
	60							2					3							4				2
56.								2				.	57.			2.							58. Сход.					59.				. 60. Расх.							61. 1/k .
56.												.	57.			2.							58. Сход.					59.				. 60. Расх.							61. 1/k .
				e ln10																										3
62.	.							63. a/(a2 b2).																64. Расх.				65. 1 ln2.							66. Расх.
67. 1/2 .									68. 8/3.											69. Расх.							70. 1/3.					71. .	72. 14						4	. 73.			.
67. 1/2 .									68. 8/3.											69. Расх.							70. 1/3.					71. .	72. 14							. 73.			.
													2																								7
74. Расх.									75.					4							.			76. Расх.				77.			Расх.		78.			.	79.									.
																	125
													3																						2
																																									3
																																									3

80.8 . 81. Сход. 82. Сход. 83. Сход. 84. Расх. 85. Расх. 86. Сход. 3


95.	It	0,99794, Is 1,00006.			96. It	0,69377,	Is	0,693152.
97.	It	0,7167, Is		0,7136.	98. It	0,99794,	Is	53,61622.
99.It		0,915728 Is		0,915965.	100.Is	1,0906.	101. It 6,0656.
Is	6,0896.		102. It 0,99794.

Г Л А В А 8

ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА

8.1. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР

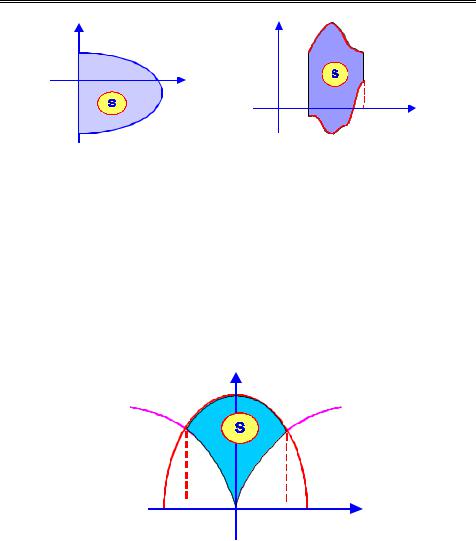
Площадь в прямоугольных координатах. а) Если непрерыв-

ная кривая задана в прямоугольных координатах уравнением y f (x) ( f (x) 0), то площадь криволинейной трапеции, ограниченной этой кривой, двумя вертикальными прямыми x a и x b ,

осью абсцисс (рис. 8.1), определяется формулой S f (x)dx.

Пример. Вычислить площадь плоской фигуры, ограниченной параболой y x2 /2, прямыми x 1 и x 3 и осью абсцисс (рис. 8.2).

Искомая площадь выражается интегралом S x2 dx 41 .

2 3

y = f (x)

		x			x
0	a	b	0	1	3
		Рис. 8.1		Рис. 8.2

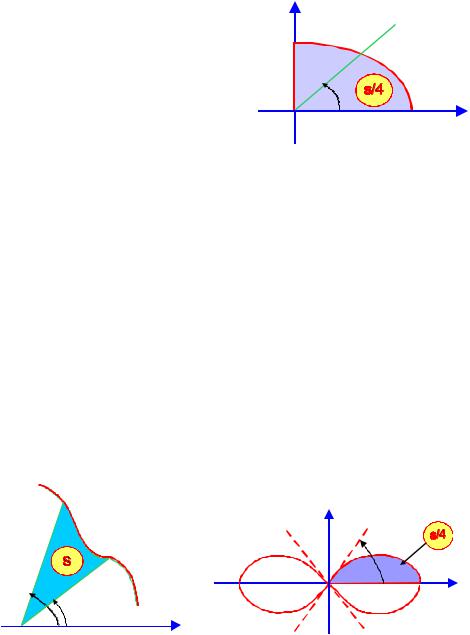
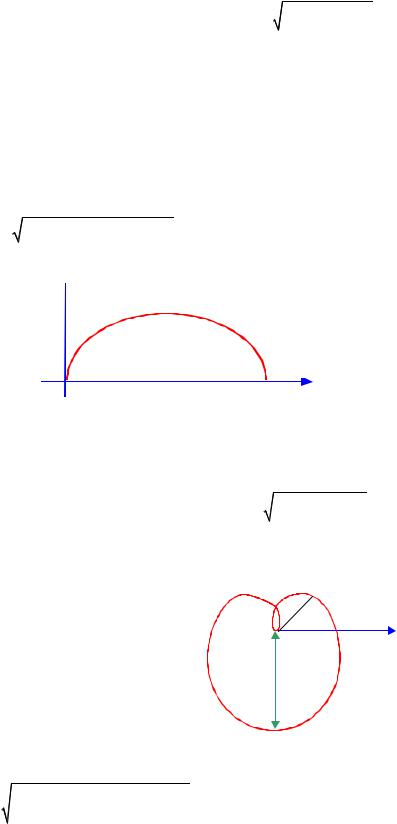
Пример. Вычислить площадь, ограниченную кривой x 2 y y2 и осью ординат (рис. 8.3).

Здесь изменены роли функции и аргумента (x f(y)) и поэто-

му искомая площадь выражается интегралом S (2 y y2)dy 4 1,

где пределы интегрирования y1 2, y2 1 найдены как ординаты точек пересечения данной кривой с осью ординат.

124	Г л а в а 8.		Геометрические и механические приложения
	у			у		у = f2(x)
		x
	0						x
					a		x
				0	a	b
						у = f1(x)
	Рис. 8.3				Рис. 8.4
б) В более общем случае,				если площадь S		ограничена двумя
непрерывными кривыми			y f1(x) и y f2(x) и двумя вертикаль-
ными	прямыми	x a,	x b ,	где	f1(x) f2(x) при		a x b
(рис. 8.4), будем иметь:
			b
		S f2(x) f1(x) dx.					(8.1)
			a
Пример. Вычислить площадь S ,					заключённую между кривы-
ми y 2 x2 и y3		x2 (рис. 8.5).
			у
		a			b


x1		0	x2
x1	Рис. 8.5		x2
	Рис. 8.5

Решая совместно систему уравнений, находим абсциссы точек пересечения данных кривых: x1 1 и x2 1. В силу формулы (8.1) получим:

1	2		2 / 3		x3	3		5 / 3	1		2
S (2 x		x		)dx 2x			x			2		.
S (2 x		x		)dx 2x	3	5	x			2	15	.
1					3	5			1		15

в) Если кривая задана уравнением в параметрической форме х = (t) y (t) , то площадь криволинейной трапеции, ограниченной этой кривой, двумя вертикальными прямыми x a, x b (а < b) и осью абсцисс, выражается интегралом:

	(8.2)
S (t) (t) dt,

8.1. Вычисление площадей плоских фигур

125

где t	1	,	t	2	определяются из уравнений a (t ),	b (t	2	)
	1			2	1		2

(t) 0, t [t , t

] .

Пример. Найти площадь, ограниченную эллипсом, используя

его параметрические уравнения: x acost,

y bsint, t [0, 2 ].

Ввиду симметрии достаточно вычислить площадь

одной

четверти (рис. 8.6). Полагая в уравнении

x acost сначала

x 0,

затем x a,

получим

пределы

интегрирования t

Поэтому

S bsint asint dt

= ab sin2 tdt

Рис. 8.6

и, следовательно,

S ab .

Площадь в полярных координатах. Если непрерывная кри-

вая задана в полярных координатах уравнением ( ), то площадь сектора AOB (рис. 8.7), ограниченного дугой кривой и двумя полярными радиусами OA и OB , соответствующими значениям

	2
	2
1 ,	2 , выразится интегралом: S	1	( ) 2 d .
1 ,	2 , выразится интегралом: S		( ) 2 d .

Пример. Найти площадь, заключённую внутри лемнискаты Бернулли 2 a2 cos2 (рис. 8.8).

В силу симметрии кривой определяем сначала площадь одной четверти искомой площади:


1			1	4					a2 1				a	2

												4
	S				a2 cos2 d						sin2				. Отсюда S a2.
4	S		2		a2 cos2 d				2	2	sin2		4		. Отсюда S a2.
4			2	0					2	2	0		4
				0

		B													y

						= ( )
						= ( )
																	4
																	4

							A
																		x

																0
0																0



								x

Рис. 8.7

Рис. 8.8

126	Г л а в а 8. Геометрические и механические приложения

Задачи для самостоятельного решения

Найти площадь плоской фигуры, ограниченной линиями:

1. y2 2x 1 и x y 1 0. 2. y2 x(x 1)2.					3. x 3t2 , y 3t t3 .
4. x2 y2 2		a2 x2 y2 и часть окружности				x2 y2 a2 /2, рас-
положенной внутри лемнискаты.
5. x t2 1, y t3 t . 6. asin2 . 7. y 4x2 3x,							y 9x .
8.	acos5 . 9.		tg ,	.	10.	y sin x ,	y cosx,

			4			y2 1 x2 3 .
часть оси абсцисс от 0 до /2.					11.
12.	y 1/(1 x2) и y x2 /2. 13. xy 6,				x y 7 0.
14.	y x2 6x 9,		x/3 y/12 1. 15.		y x3, y 2x, y x.
16.	y ex ,	y e x,	x 1. 17. y2 9x, x2			9y.
18. a(1 cos ).			19. 2 cos .

20.(x2 y2)2 a2(4x2 y2) .

8.2.ВЫЧИСЛЕНИЕ ДЛИНЫ ДУГИ ПЛОСКОЙ КРИВОЙ

Длина дуги кривой в прямоугольных координатах. Длина l

дуги гладкой кривой y y(x), содержащейся между двумя точка-

ми с абсциссами x a и x b , (а < b), равна l 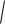1 (y/)2dx.

Пример.Найти длинудуги астроиды x2/3 y2/3 a2/3 (рис. 8.9).

y1/3

Дифференцируя уравнение астроиды, получаем: y/ x1/3 .

Поэтому для длины дуги одной чет-

верти астроиды имеем:

a a1/3

y2/3

1/4l

x2/3

x1/3

Отсюда l 6a .

Длина дуги кривой, заданной

параметрически. Если кривая задана

параметрически

уравнениями:

Рис. 8.9

x x(t)

и y y(t), t [t1, t2] ( x(t) и

y(t) –

непрерывно дифференцируе-

8.2. Вычисление длины дуги плоской кривой			127
t2
t2	x/2	(t) y/2
мые функции), то длина дуги кривой равна l	x/2	(t) y/2	(t) dt ,
t1

где t1, t2 – значения параметра, соответствующие концам дуги.

Пример. Найти длину одной арки циклоиды (рис. 8.10)

xa(t sint), y a(1 cost).

Одной арке циклоиды соответствует изменение параметра t

от 0 до 2 . Имеем x/		dx	a(1 cost) и	y/	dy		asint . Поэтому
		dt			dt
2				2		t
l	a2(1 cost)2		a2 sin2 tdt 2a sin			t	dt 8a . #
l	a2(1 cost)2		a2 sin2 tdt 2a sin			2	dt 8a . #
0				0

0	2 а
	2 а
	Рис. 8.10

Длина дуги кривой, заданной в полярной системе координат.

Если кривая задана уравнением ( ),

[ , ] в полярных ко-

2( ) /2

ординатах,

то длина дуги кривой l

равна l

( )

d ,

где , – значения полярного угла в крайних точках дуги.

Пример.

Найти

длину

кривой,

( , )

заданной

уравнением

a sin3

(рис. 8.11).

Вся кривая описывается дви-

жением

точки

( , )

при

измене-

нии

от

0 до 3 . Имеем

( )=

asin2

cos

поэтому длина всей

Рис. 8.11

дуги кривой равна

3 a

a2 sin6

a2 sin4

cos2

d a sin2

128	Г л а в а 8. Геометрические и механические приложения

Задачи для самостоятельного решения

21. Вычислить длину дуги полукубической параболы y2 2(x 1)3,

заключенной внутри параболы y2 x . 3

22. На циклоиде x a(t sint), y a(1 cost) найти точку, ко-

торая делит длины дуг первой арки циклоиды в отношении 1:3. 23. Найти длину дуги кардиоиды: a(1 cos ) .

24. Найти длину дуги полукубической параболы 5y3 x2 , за-

ключенной внутри окружности x2 y2 6.

25. Найти длину петли линии x t2 ,

y t t3 /3.

26. Найти длину дуги кривой y ex , содержащейся между точ-

ками M1(0; 1) M2(1; e).

27. Вычислить длину замкнутой части кривой 9ay2 x(x 3a)2.

28. Вычислить длину первого витка спирали Архимеда a

(a > 0).
29. Найти длину дуги кривой	1		1
		1		от 1 до			3.

2

30. Найти длину дуги линии y		x x2 arcsin				.
					x
8.3. ВЫЧИСЛЕНИЕ ОБЪЕМОВ ПРОСТРАНСТВЕННЫХ ТЕЛ
Объем тел вращения. а) Объем тела, образованного							враще-

нием вокруг оси Ox криволинейной трапеции, ограниченной кривой, заданной уравнением y y(x), где y(x)–непрерывная одно-

значная функция на [a, b] Ox (или кривой, заданной уравнением

x x(y), где	x(y)– строго монотонная функция на[c, d] Oy , при
этом x(c) a,	x(d) b), осью Ox и	прямыми x a,	x b	вычис-
ляется по одной из формул:
	b
	Vx y2(x)dx			(8.3)
	a

или

d
Vx	y2 x/ (y)dy .	(8.4)
c

б) Объем тела, образованного вращением вокруг оси Oy криволинейной трапеции, ограниченной кривой, заданной уравнением

8.3. Вычисление объемов пространственных тел					129
x x(y), где х(у) – однозначная			непрерывная функция на [c, d] Oy
(или кривой, заданной уравнением				y y(x),	где y(x)– строго мо-
нотонная	функция на	[a, b] Ox,		при этом	y(a) c , y(b) d ),
осью Oy	и прямыми	y c, y d , вычисляется по одной из фор-
мул:
		d
		Vy	x2(y)dy		(8.5)
или		c
или
		b
		Vy	x2 y/ (x)dx.		(8.6)
		a

Если кривая, ограничивающая трапецию, задана в иной форме (параметрически, в полярных координатах и т.п.), то в приведенных выше формулах (8.3)–(8.6) необходимо сделать соответствующую

замену переменной интегрирования.
		Пример. Вычислить объемы тел, полученных вращением фи-
гуры, ограниченной линиями							y sin x						x [0; /2], x /2, осью
Ox	вокруг:
		а) оси Ox ; б) оси Oy .
							/ 2									/ 2				2
	а) По формуле (8.3) V										sin2		dx					(1 cos 2x)dx			.
	а) По формуле (8.3) V										sin2		dx					(1 cos 2x)dx			.
						x							2							4
						x
									0								0
		б)	Так как функция y(x) sin x – строго монотонная на отрез-

ке	[0; /2],			то по формуле (8.6)						имеем Vy x2 cosx dx (ин-
																	0
															/	2			/ 2
															/	2			/ 2
тегрируем по частям дважды)							(x2 sin x)										2			x sin xdx
															0			0
					/ 2	/ 2								( 2		8)
					/ 2	/ 2

			2	x cos x			cos xdx												.
			2	x cos x			cos xdx												.
	4												4
					0	0														y(x) sin x,
					0	0
Заметим, что в силу строгой монотононости функции
x [0; /2]				можно записать			x(y) arcsin y,										y [0; 1], тогда по
формуле (8.5) получим:
				1			(	2		8)
			Vy arcsin2 ydy				(			8)		,	V Vцил Vy
			Vy arcsin2 ydy					4				,	V Vцил Vy
				0				4
				0

(подстановкой arcsin y x последний интеграл приводится к вы-

численному ранее).

130 Г л а в а 8. Геометрические и механические приложения

в) В более общем случае объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной осью Ox и линиями x a,

x b, y y1(x),

y y2(x) , где y1(x), y2(x) – непрерывные неотри-

цательные функции ( y1(x) y2(x)

x [a; b]),

равен

Vx y2 (x) y1

(x) dx.

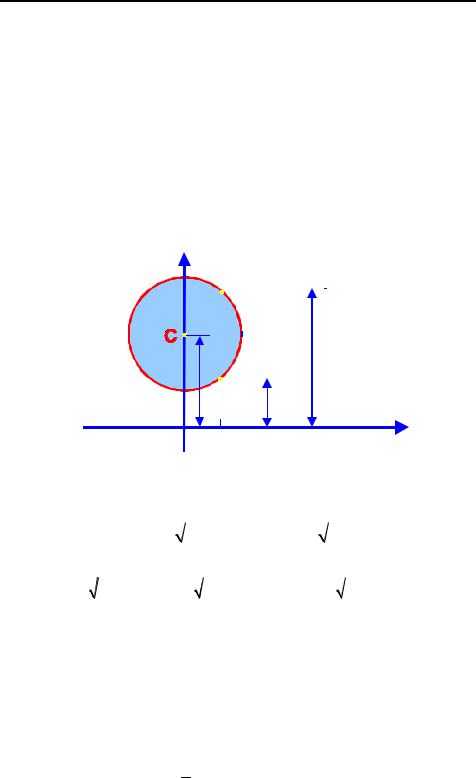
Пример. Найти объем тора,

образованного вращением круга

x2 (y b)2 a2

(a b)

вокруг оси Ox (рис. 8. 12).

у2

у1

-a

Рис. 8.12

Имеем:

y1 b

a2 x2

y2 b

x2 . Поэтому

a2 x2dx 2 2a2b

b a2 x2

dx 4 b

(последний интеграл берется подстановкой x asint ).

Объем тела, полученного при вращении сектора, ограни-

ченного дугой кривой ( ) и двумя полярными радиусами, вокруг полярной оси, может быть вычислен по формуле:

V 2 3( ) sin d . 3

Пример. Определить объем, образованный вращением кривойasin2 вокруг полярной оси

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1819 / 2119 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
26.08.20191.86 Mб12Матем.-1.doc
#
14.08.20191.26 Mб7Матем.-1.doc
#
27.03.20154.27 Mб66Матем.-6.doc
#
27.03.20151.18 Mб18Матем.-7.doc
#
27.03.2015183.74 Кб25Математическая логика.docx
#
27.03.20152.2 Mб637Математический анализ в примерах и задачах.pdf
#
21.07.2019598.66 Кб8материалка.docx
#
27.03.20153.32 Mб57Материаловедение.pdf
#
27.03.20151.79 Mб43Материаловедение_Лаб_раб.doc
#
16.09.2019712.19 Кб6Материаловедение_ММ.doc
#
21.08.2019153.09 Кб4Материалы к семинару.doc