
2012_МА_часть_1_методические рекомендации
.pdf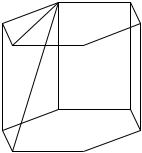
верным ответом без приведения сколько-нибудь развернутых вычислений. Приведем конкретный пример из ЕГЭ–2011.
В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , |
|
E1 |
|
D1 |
|||||
стороны основания которой равны 5, а боковые ребра |
|
|
|||||||
F1 |
|
C1 |
|||||||
равны 11, |
найдите расстояние от точки |
A до прямой |
|
A1 |
B1 |
||||
E1 D1 . |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
Это расстояние, см. рис., равно AE1 |
=14 . |
|
|
|
|
|
|
||
Ответ: 14. |
|
|
|
|
|
|
E |
|
D |
По |
критериям |
двух предыдущих |
лет |
– это |
F |
|
|
C |
|
A |
B |
||||||||
0 баллов, |
так как |
решение не |
содержит |
никакого |
|
|
|
|
|
обоснованного перехода куда-либо, а по критериям ЕГЭ–2012 – это 1 балл именно из-за дополнения «… или при правильном ответе решение недостаточно обосновано».
Конечно, это довольно экзотическая в процентном отношении ситуация, но при переходе к количеству реальных участников ЕГЭ речь идет о десятках тысяч работ.
Еще раз повторим, дополнение «… или при правильном ответе решение недостаточно обосновано» введено не для того, чтобы «зарубить» двухбалльные решения, массово выставив за них 1 балл, а, наоборот, для того, чтобы иметь в некоторых случаях возможность повысить оценку с 0 до 1 балла.
Необходимо отметить еще одно существенное обстоятельство, связанное с использованием в решении заданий С2 элементов аналитической геометрии (координаты точек, уравнения плоскостей и прямых т.п.). Так как получение формул, скажем, для тех или иных расстояний основано, в конечном счете, на сведении к соответствующей планиметрической задаче, то верное использование этих формул автоматически подразумевает обоснованное сведение к планиметрической задаче. Тем самым, критерий на 1 балл нормально работает и в применении к тем случаям, когда правильно используется верная формула аналитической стереометрии, но в вычислениях содержится арифметическая ошибка.
21

Примеры оценивания выполнения заданий С2
Задача С2 – 1.
Ребро куба ABCDA1 B1C1 D1 равно |
1. Найдите расстояние от вершины В до |
|||||||||||||||
плоскости ACD1 . |
|
|
|
|
|
|
|
|
||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Прямая AC перпендикулярна плоскости BDD1 , |
|
|
||||||||||||
так как она перпендикулярна прямым BD и DD1 . |
|
|
||||||||||||||
Плоскость ACD1 содержит прямую AC , следовательно, |
|
|
||||||||||||||
плоскости BDD1 и ACD1 перпендикулярны. Тогда |
|
|
||||||||||||||
расстояние от точки B до плоскости ACD1 |
есть высота |
|
|
|||||||||||||
треугольника BOD1 , проведенная из вершины B . |
|
|
|
|
||||||||||||
|
|
В треугольнике BOD1 : BD1 = |
3 , BO = |
|
2 |
, OD1 = |
6 |
. |
|
|
||||||
|
2 |
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Из |
треугольников |
BHO |
|
и |
BHD1 : |
|
|
|||||||
BH 2 = BO2 −OH 2 = BD12 −(OD1 +OH )2 , |
откуда |
|
получаем: |
|
|
|||||||||||
OH = |
6 |
, тогда получаем: BH = |
3 |
. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||
6 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||
Ответ: |
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Содержание критерия |
|
|
Баллы |
|||||||
|
Обоснованно получен верный ответ |
|
|
|
|
2 |
|
|||||||||
|
Решение содержит обоснованный переход к планиметрической |
1 |
|
|||||||||||||
|
задаче, но получен неверный ответ или решение не закончено, |
|
||||||||||||||
|
Или при правильном ответе решение недостаточно обосновано |
|
|
|||||||||||||
|
Решение |
не соответствует |
ни одному |
из критериев, |
0 |
|
||||||||||
|
перечисленных выше |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Максимальный балл |
2 |
|
||
22

Пример 1.
Ребро куба ABCDA1B1C1D1 равно 1. Найдите расстояние от вершины В до плоскости ACD1 .
Ответ:  33 .
33 .
Комментарий. Работа не пустая, и ответ верен. Тем не менее в работе не прослеживается правильного геометрического представления о происходящем. На самом деле, основание перпендикуляра попадает не на сторону D1O , а на ее продолжение. В тексте имеется явно неверное
утверждение. А именно, если «H – точка пересечения медиан …», то
неверно, что BH AD1C .
Оценка эксперта: 0 баллов.
23
Пример 2.
Ребро куба ABCDA1B1C1D1 равно 1. Найдите расстояние от вершины В до плоскости ACD1 .
Ответ:  33 .
33 .
Комментарий.
Как и в предыдущем примере, рисунок не соответствует действительности. Но, и это существенно, в тексте решения отсутствуют неверные утверждения, а ссылок на неверный рисунок – нет.
Оценка эксперта: 2 балла.
24
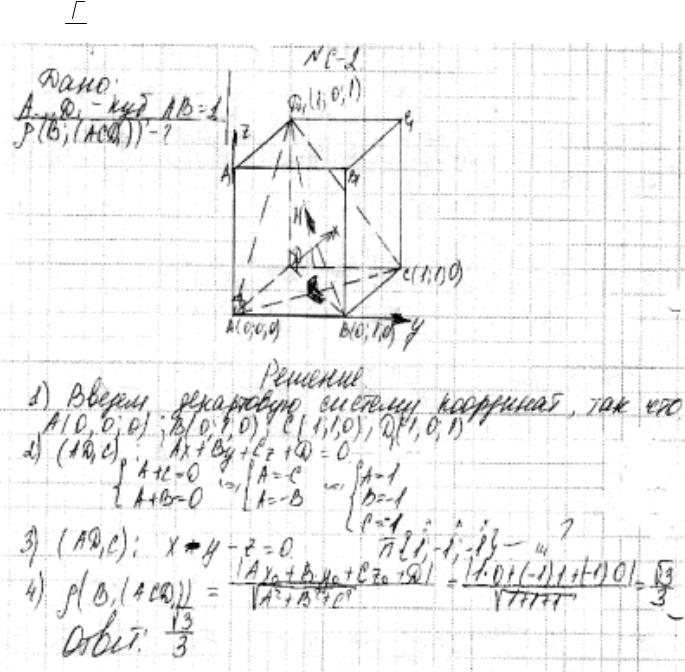
Пример 3.
Ребро куба ABCDA1B1C1D1 равно 1. Найдите расстояние от вершины В до плоскости ACD1 .
Ответ:  33 .
33 .
Комментарий.
В работе всюду написано не про расстояние от точки до плоскости, а про расстояние от плоскости до точки, но в остальном – верно.
Оценка эксперта: 2 балла.
25
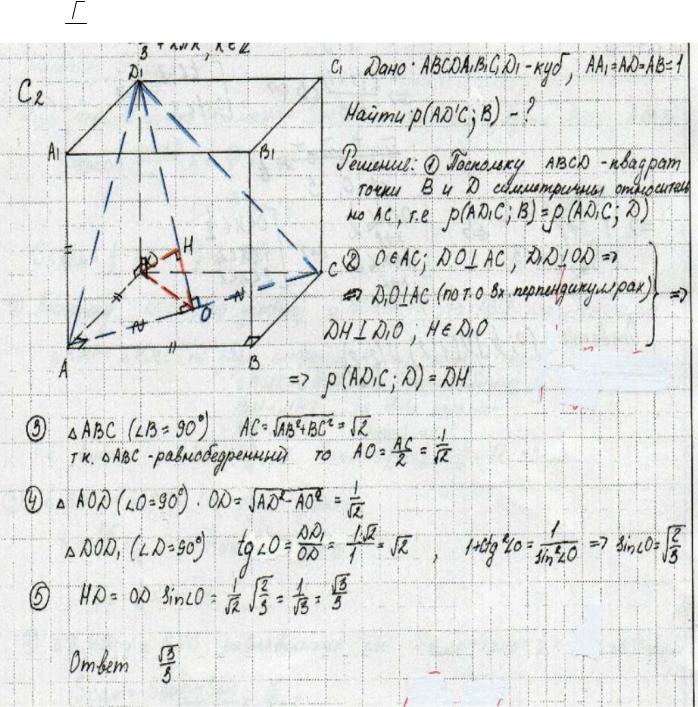
Пример 4.
Дан куб ABCDA1B1C1D1 . Длина ребра куба равна 1. Найдите расстояние от середины отрезка BC1 до плоскости AB1D1 .
Ответ:  33 .
33 .
Комментарий. Утверждение MB1 AD1D1 неверно: AB1M – не прямой угол. Подсчеты верны, но вычисляется не то, что нужно.
Оценка эксперта: 0 баллов.
26

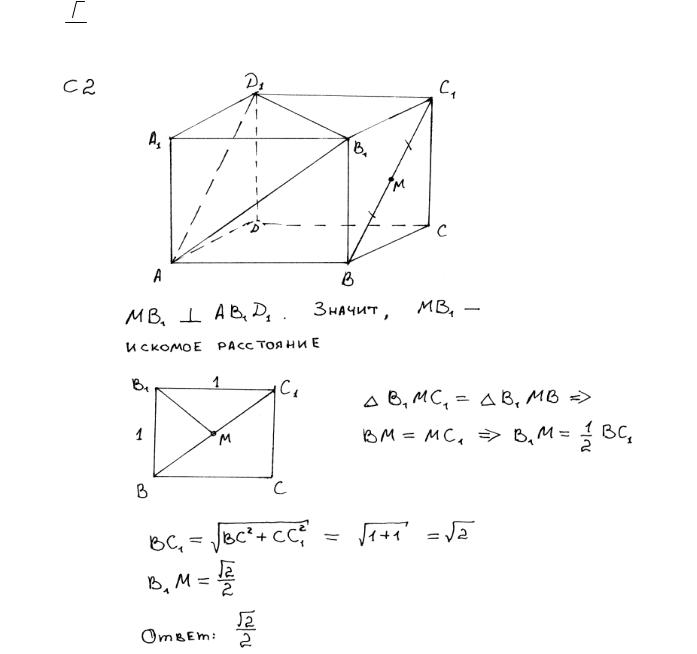
Пример 5.
Дан куб ABCDA1B1C1D1 . Длина ребра куба равна 1. Найдите расстояние от середины отрезка BC1 до плоскости AB1D1 .
Ответ:  33 .
33 .
Комментарий. Что-то есть, но неверно, что «искомое расстояние = MN».
Оценка эксперта: 0 баллов.
27
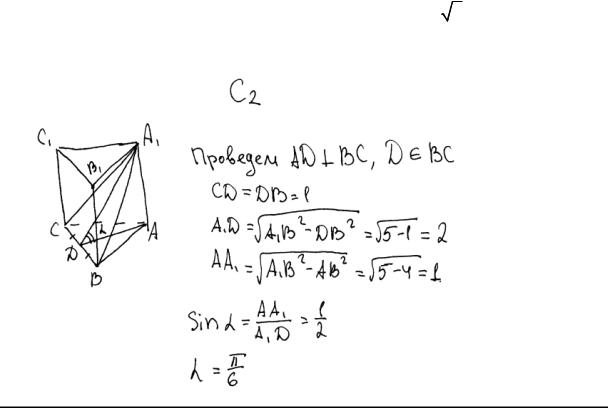
Пример 6. Сторона основания правильной треугольной призмы ABCA1B1C1
равна 2 , а диагональ боковой грани равна 5 . Найдите угол между плоскостью A1BC и плоскостью основания призмы.
Ответ: 30.
Комментарий. Типичный случай, когда нет «идеальной» проверки того, чтоA1DA – искомый линейный угол, но все построения и вычисления верны.
Оценка эксперта: 2 балла.
28

Пример 7. Найти угол между прямой, проходящей через середины скрещивающихся ребер правильной треугольной пирамиды и плоскостью ее основания. Боковое ребро равно 29, сторона основания 20 3 .
3 .
Ответ: arctg 4021 .
Комментарий. Прямо по критериям: «Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ…»
Оценка эксперта: 1 балл.
29
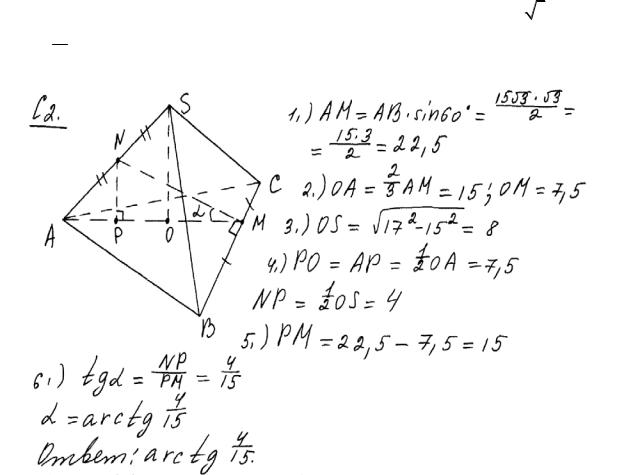
Пример 8. Найти угол между прямой, проходящей через середины скрещивающихся ребер правильной треугольной пирамиды, и плоскостью ее
основания. Боковое ребро равно 17, сторона основания равна 15 3 .
Ответ: arctg 154 .
Комментарий.
В целом – похоже на предыдущий пример. Но, в отличие от него, здесь вычисления логичны, выбран разумный способ подсчета через тангенс и, самое главное, вычисления не содержат ошибок.
Оценка эксперта: 2 балла.
30
