
ПриклТеорияКолеб
.pdf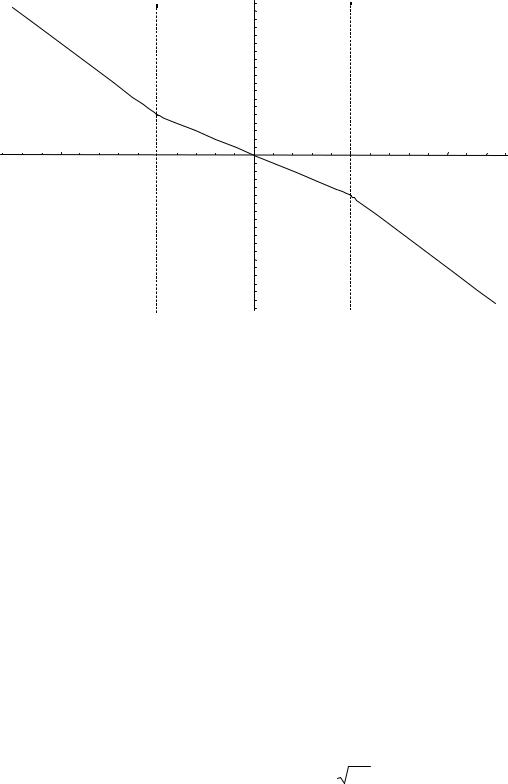
14
|
|
|
Q |
|
|
|
|
7.5 |
|
|
|
|
III |
5 |
II |
I |
|
|
|
|
|
|
|
|
|
2.5 |
|
|
|
0.2 |
0.1 |
|
0.1 |
0.2 |
q |
|
|
|
|
|
|
|
|
2.5 |
|
|
|
|
|
|
|
|
|
5
7.5
Рис. 5
2.2.Интегрирование уравнения движения по методу припасовывания
Вначальном положении система находится на участке I (q0>s/a). Следовательно, начинаем интегрирование уравнения движения с этого участка.
Участок I (q>s/a). |
|
Дифференциальное уравнение движения |
|
q + k 2q = −σ. |
(4) |
1 |
|
Это линейное неоднородное дифференциальное уравнение второго порядка. Для упрощения его решения воспользуемся заменой переменных q=q1-d, где d определим из условия, чтобы новое уравнение стало однородным:
q |
+ k |
2q = 0. |
|
(5) |
1 |
1 |
1 |
|
|
Для этого необходимо принять d = σ/ k 2 |
= 0.0445рад. |
|||
|
|
1 |
|
|
Начальные условия |
|
|
||
q10 = q0 + d = 0,2445 рад, q10 = q0 = 0. |
(6) |
|||
Для решения уравнения (5) составим характеристическое уравнение |
||||
z 2 + k 2 = 0. |
|
|
||
|
|
1 |
|
|
Корни этого уравнения мнимые (z1,2 = ±k1i, i = |
−1) , и решение записыва- |
|||
ется через тригонометрические функции |
|
|
||
q1 = α1 cos(k1t + δ1). |
|
(7) |
||
Для определения произвольных постоянных интегрирования α1 и δ1 нахо-
дим скорость движения.

15
q1 = −α1k1 sin(k1t + δ1).
Полагая, что в начальный момент t0 = 0 , и используя условия (6), получим систему двух уравнений
q10 = α1 cos δ1,
0 = −α1k1 sin δ1.
Второе из этих уравнений показывает, что можно принять δ1 = 0.Тогда из первого уравнения находим α1 = q10.Переходя к исходной переменной q,
запишем частное решение дифференциального уравнения на участке I:
q = α1 cos k1t − d, q = −k1α1 sin k1t.
Исключая из системы этих двух уравнений время, приходим к интегральной кривой, которая в данном случае совпадает с фазовой траекторией
(q + d )2 |
+ |
|
q2 |
=1. |
|
α 2 |
k 2α 2 |
||||
|
|
||||
1 |
|
1 |
1 |
|
|
Получили уравнение эллипса, центр которого смещен от начала координат на расстояние d влево вдоль оси q. Естественно, только часть эллипса, лежащая в зоне I, изображена как часть фазовой траектории (см. рис. 6).
Определим время движения t1 в зоне I, учитывая, что для т. А1 q=s/a. По уравнению движения запишем
s / a = α1 cos k1t1 − d,
откуда
|
1 |
|
1 |
s |
|
|
|||
t = |
|
arccos |
|
|
|
|
|
+ d |
. |
k |
α |
|
|
||||||
1 |
|
1 |
a |
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
Находим численное значение t1=0,0885 c. |
|
Значения координаты и скорости в этот момент |
|
q20 = s / a = 0.1 рад, q20 = −2.09 рад/с |
(8) |
являются начальными значениями для построения решения дифференциального уравнения движения на участке II. Этот переход от участка I к участку II и составляет суть метода припасовывания или сшивки решений.
Участок II (q < s / a).
Согласно (3), уравнение движения на этом участке имеет вид
q + k2q = 0 |
(9) |
при начальных условиях вида (8). Это уравнение следует решать так же, как и уравнение (5). Поэтому запишем его общее решение в виде (7):
q = α2 cos(k2t + δ2 ).
Для определения α2 и δ2 запишем систему уравнений

|
|
|
|
|
|
|
|
|
|
|
16 |
q |
20 |
= α |
2 |
cos δ |
2 |
, |
|
(10) |
|||
|
|
|
|
|
|
|
|||||
q20 |
= −α2k2 sin δ2 . |
|
|||||||||
Разделив второе уравнение на первое, находим |
|||||||||||
|
|
|
|
|
|
q |
20 |
|
|
||
δ2 |
|
|
|
|
− |
|
|
δ2 =1.21 рад. |
|||
|
|
|
|
|
|||||||
|
= arctg |
k2 q20 |
, |
||||||||
|
|
|
|
|
|
|
|
||||
Из второго из записанных уравнений (10) получим α2 = 0.283 рад.
Частное решение на участке II приобретает вид q = 0.283cos(7.9t +1.21).
Отметим, что время отсчитывается от момента, когда угол q был равен s/a. Находим время прохождения положения равновесия
7,9t2 +1,21 = π2 , t2 = 0.0455 c .
Следовательно, период колебаний составит
T = 4(t1 + t2 )= 0.536 c.
Скорость движения системы
q = −2.24sin(7.9t +1.21).
Фазовая траектория является участком эллипса
q2 + q2 =1. 0.2832 2.242
На остальных участках фазовую траекторию строим, используя свойства симметрии (рис.6).
q
2
1
|
|
0.1 |
0.2 |
|
0.2 |
0.1 |
q |
||
|
|
|
|
1
2
Рис. 6
17
При решении задачи в соответствии с заданным вариантом использовать следующие числовые значения:
m1 = 4 кг, m2 = 2 кг, c = c1 =8 Н/см, c2 =12 Н/см, s=2 см, r=0,2 м, R=0,4 м, α = 20°, β = 20° (для рис. 3 и 22 β = 70°), d=0,1 м, b=0,2 м, l=0,3 м (для рис.
1 и 2 b=0,3 м, l=0,2 м). Радиусы цилиндров равны 0,1 м (рис. 8, 12, 13, 17, 18, 30) или 0,2 м (рис. 9, 23, 25, 28). Если на рисунке изображено одно подвижное тело, массу принять равной m1.
Пружины в положении равновесия сжаты на 2 см (рис. 3, 4, 9, 10, 11, 16, 21, 22, 29). На рис. 14 в изображенном положении пружина не напряжена и связь между телом и пружиной не удерживающая (т.е., при движении тела вверх пружина не растягивается).
Радиусы инерции вращающихся тел на рис. 8, 12, 17, 30 и катков на рис. 20, 21, 24, 29 принять равными 0,1 м. Радиус инерции тела на рис. 2 равен 0,25м. В остальных случаях стержни и цилиндры считать однородными.
Механизмы считать расположенными в горизонтальной плоскости. Начальные условия:
для рис. 1, 2, 5, 7, 8, 9, 12, 13, 14, 15, 18, 20, 23, 24, 25, 26, 28, 29, 30 Тип А: q0 = 0,15 рад, q0 = 0 ;
Тип Б: q0 = 0, q0 = 4 рад/с;
Тип В: q0 = 0,1 рад, q0 = 2 рад/с;
для рис. 3, 4, 6, 10, 11, 16, 17, 19, 21, 22, 27
Тип А: q0 = 0,05 м, q0 = 0 ;
Тип Б: q0 = 0, q0 = 0,4 м/с;
Тип В: q0 = 0,03 м, q0 = 0,2 м/с.
18
ЗАДАЧА 3
Исследование свободных и вынужденных колебаний механической системы с двумя степенями свободы
Условие задачи.
Механическая система с двумя степенями свободы состоит из нескольких тел с массами mi. На схемах (см. рисунки на с. 33–36) указаны радиусы колес Ri, коэффициенты жесткости пружин или валов ci. Кинетической энергией скручиваемых валов и потенциальной энергией сил тяжести пренебречь. Колеса и стержни – сплошные однородные тела. Необходимо:
1)составить уравнения движения механической системы;
2)определить частоты свободных колебаний;
3)найти формы главных колебаний системы;
4)найти закон движения механической системы, если известно, что в начальный момент времени тела 1 и 2 были отклонены от положения равновесия
на углы ϕ10 и ϕ20 (или смещены на расстояния x10 и x20 ), соответственно, и имели угловые скорости ϕ10 и ϕ20 (или линейные скорости x10 и x20 );
5)пренебрегая сопротивлением, исследовать вынужденные колебания сис-
|
темы |
под действием гармонического |
|
возмущения |
в |
|
|
виде |
|
|
момента |
|||||||||||||||||||||||||||||||||||
|
M = M0 sin ωt; рисунки на стр. 40–43. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
Варианты условий для рис. 1, 4, 5, 9, 16, 21, 24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
№ |
|
|
m1, |
|
m2, |
|
c1, |
|
c2, |
|
c3, |
, м |
|
ϕ10, |
|
ϕ20, |
|
ϕ |
|
|
, |
|
|
|
ϕ |
20 |
, |
|
ϕ1стат, |
||||||||||||||||
|
|
|
|
кг |
|
|
|
|
кг |
|
Н/см |
|
Н/см |
Н/см |
|
|
|
рад |
|
рад |
|
10 |
|
|
|
|
|
|
|
|
|
|
рад |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рад/с |
|
|
|
рад/с |
|||||||||||||||||||||||||||
|
1 |
|
|
1 |
|
|
|
2 |
|
40 |
|
30 |
|
|
20 |
0,5 |
|
|
0 |
|
|
0,01 |
|
0,1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
0,03 |
|
||||||||
|
2 |
|
|
2 |
|
|
|
1,5 |
|
30 |
|
40 |
|
|
20 |
0,4 |
|
|
0,02 |
|
0 |
|
|
0,15 |
|
|
|
|
|
|
0 |
|
|
|
|
0,02 |
|
|||||||||
|
3 |
|
|
1,2 |
|
|
1 |
|
25 |
|
30 |
|
|
40 |
0,6 |
|
|
0 |
|
|
0,02 |
|
|
0 |
|
|
|
|
|
0,1 |
|
|
|
|
0,01 |
|
||||||||||
|
4 |
|
|
1 |
|
|
|
1,5 |
|
35 |
|
20 |
|
|
30 |
0,5 |
|
|
0,01 |
|
0 |
|
|
|
0 |
|
|
|
|
|
0,2 |
|
|
|
|
0,03 |
|
|||||||||
|
5 |
|
|
1,2 |
|
|
1,8 |
|
40 |
|
25 |
|
|
35 |
0,4 |
|
|
0 |
|
|
0,01 |
|
0,1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
0,02 |
|
|||||||||
|
Варианты условий для рис. 2 (рамка состоит из 3 одинаковых стержней) |
|||||||||||||||||||||||||||||||||||||||||||||
|
№ |
m1, |
|
m2, |
|
m3, |
|
c1, |
|
c2, |
, |
R, |
|
ϕ10, |
|
ϕ20, |
|
|
ϕ |
|
, |
|
|
|
ϕ |
20 |
, |
|
|
|
|
ϕ1стат, |
||||||||||||||
|
|
|
кг |
|
кг |
|
кг |
|
Н/см |
|
Нм/рад |
м |
м |
|
рад |
|
рад |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
рад |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
рад/с |
|
|
|
рад/с |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
5 |
|
2 |
|
1 |
|
|
400 |
|
|
3 103 |
1,0 |
0,1 |
|
0 |
|
0,01 |
|
0,1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0,03 |
|
|||||||||||
2 |
4 |
|
1,5 |
|
2 |
|
|
300 |
|
|
4 103 |
0,8 |
0,2 |
|
0,02 |
|
0 |
|
0,15 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0,02 |
|
||||||||||||
3 |
5 |
|
1 |
|
1,2 |
|
|
250 |
|
|
3 103 |
0,8 |
0,1 |
|
0 |
|
0,02 |
|
0 |
|
|
|
|
0,1 |
|
|
|
|
|
0,01 |
|
|||||||||||||||
4 |
4 |
|
1,5 |
|
1 |
|
|
350 |
|
|
2 103 |
1,0 |
0,2 |
|
0,01 |
|
0 |
|
0 |
|
|
|
|
0,2 |
|
|
|
|
|
0,03 |
|
|||||||||||||||
5 |
5 |
|
1,8 |
|
1,2 |
|
|
400 |
|
|
2 103 |
0,9 |
0,1 |
|
0 |
|
0,01 |
|
0,1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0,02 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Варианты условий для рис. 3, 20, 23, 25, 26 |
|||||||||||||||||||||||||||
|
№ |
|
|
m1, |
|
|
|
m2, |
|
|
c1, |
|
|
c2, |
|
c3, |
, м |
|
ϕ10, |
|
x20, |
|
ϕ |
|
|
, |
|
|
|
|
x |
20 |
, |
|
|
ϕ1стат, |
|
|||||||||
|
|
|
|
кг |
|
|
|
кг |
|
|
Н/см |
|
|
Н/см |
Н/см |
|
|
|
рад |
|
см |
10 |
|
|
|
|
|
|
|
|
|
|
рад |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рад/с |
|
|
|
см/с |
|
|
|
|
||||||||||||||||||||||
|
1 |
|
1 |
|
|
|
|
2 |
|
40 |
|
30 |
|
|
20 |
0,5 |
|
0 |
|
0,3 |
|
0,1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
0,03 |
|
||||||||||
|
2 |
|
2 |
|
|
|
|
1,5 |
|
30 |
|
40 |
|
|
20 |
0,4 |
|
0,02 |
|
0 |
|
0,15 |
|
|
|
|
|
|
0 |
|
|
|
|
|
0,02 |
|
||||||||||
|
3 |
|
1,2 |
|
|
|
1 |
|
25 |
|
30 |
|
|
40 |
0,6 |
|
0 |
|
0,2 |
|
0 |
|
|
|
|
|
0,1 |
|
|
|
|
0,01 |
|
|||||||||||||
|
4 |
|
1 |
|
|
|
|
1,5 |
|
35 |
|
20 |
|
|
30 |
0,5 |
|
0,01 |
|
0 |
|
0 |
|
|
|
|
|
0,2 |
|
|
|
|
0,03 |
|
||||||||||||
|
5 |
|
1,2 |
|
|
|
1,8 |
|
40 |
|
25 |
|
|
35 |
0,4 |
|
0 |
|
0,5 |
|
0,1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
0,02 |
|
|||||||||||
19
Варианты условий для рис. 6, 12, 15, 18, 27 – 29 (для рис. 18: m3 = m2= m1)
|
|
№ |
|
|
|
m1, кг |
|
m2, кг |
|
c1, |
|
|
c2, |
|
|
|
c3, |
|
|
|
|
x10, |
|
|
x20, |
|
|
x10 , |
|
|
|
x20 , |
|
|
x1стат, |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н/см |
|
|
Н/см |
|
|
Н/см |
|
|
|
см |
|
|
|
см |
|
см/с |
|
|
|
см/с |
|
|
см |
|
|
||||||||||||||||||
|
|
1 |
|
|
|
|
|
6 |
|
|
2 |
|
|
|
|
|
40 |
|
|
|
30 |
|
|
20 |
|
|
|
0 |
|
|
0,3 |
|
|
0,1 |
|
|
|
|
0 |
|
|
|
|
0,3 |
|
|
||||||||||||||||
|
|
2 |
|
|
|
|
|
5 |
|
|
1,5 |
|
|
|
30 |
|
|
|
40 |
|
|
20 |
|
|
|
0,2 |
|
|
0 |
|
|
0,15 |
|
|
|
|
0 |
|
|
|
|
0,2 |
|
|
||||||||||||||||||
|
|
3 |
|
|
|
|
|
4 |
|
|
1 |
|
|
|
|
|
25 |
|
|
|
30 |
|
|
40 |
|
|
|
0 |
|
|
0,2 |
|
|
0 |
|
|
|
0,1 |
|
|
0,1 |
|
|
|||||||||||||||||||
|
|
4 |
|
|
|
|
|
6 |
|
|
1,5 |
|
|
|
35 |
|
|
|
20 |
|
|
25 |
|
|
|
0,1 |
|
|
0 |
|
|
0 |
|
|
|
0,2 |
|
|
0,3 |
|
|
|||||||||||||||||||||
|
|
5 |
|
|
|
|
|
5 |
|
|
1,8 |
|
|
|
40 |
|
|
|
25 |
|
|
30 |
|
|
|
0 |
|
|
0,5 |
|
|
0,1 |
|
|
|
|
0 |
|
|
|
|
0,2 |
|
|
||||||||||||||||||
|
|
|
|
|
Варианты условий для рис. 7, 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
№ |
|
|
|
m1, |
|
|
m2, |
|
|
c1, |
|
|
|
c2, |
|
c3, |
|
|
|
, м |
|
|
x10, |
|
|
ϕ20, |
|
x |
, |
|
|
|
ϕ |
20 |
, |
|
|
x1стат, |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
кг |
|
|
кг |
|
|
Н/см |
|
|
Н/см |
Н/см |
|
|
|
|
|
|
|
|
см |
|
|
|
рад |
|
|
10 |
|
|
|
|
|
|
|
|
см |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
см/с |
|
|
рад/с |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
6 |
|
|
|
2 |
|
|
40 |
|
|
|
30 |
|
20 |
|
|
0,5 |
|
|
0,3 |
|
|
0 |
|
|
0 |
|
|
|
0,1 |
|
|
0,3 |
|
|
||||||||||||||||||||
|
|
2 |
|
|
|
|
|
5 |
|
|
|
1,5 |
|
|
30 |
|
|
|
40 |
|
20 |
|
|
0,4 |
|
|
0 |
|
|
0,02 |
|
|
0 |
|
|
|
0,15 |
|
|
0,2 |
|
|
||||||||||||||||||||
|
|
3 |
|
|
|
|
|
4 |
|
|
|
1 |
|
|
25 |
|
|
|
30 |
|
40 |
|
|
0,6 |
|
|
0,2 |
|
|
0 |
|
|
0,1 |
|
|
|
|
|
0 |
|
|
|
|
0,1 |
|
|
||||||||||||||||
|
|
4 |
|
|
|
|
|
6 |
|
|
|
1,5 |
|
|
35 |
|
|
|
20 |
|
30 |
|
|
0,5 |
|
|
0 |
|
|
0,01 |
|
|
0,2 |
|
|
|
|
|
0 |
|
|
|
|
0,3 |
|
|
||||||||||||||||
|
|
5 |
|
|
|
|
|
5 |
|
|
|
1,8 |
|
|
40 |
|
|
|
25 |
|
35 |
|
|
0,4 |
|
|
0,5 |
|
|
0 |
|
|
0 |
|
|
|
0,1 |
|
|
0,2 |
|
|
||||||||||||||||||||
|
|
|
|
|
Варианты условий для рис. 10, 13 (для рис. 10: m4 = m2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
№ |
m1, |
|
m2, |
|
m3, |
|
|
|
c1, |
|
|
|
|
|
c2, |
|
c3, |
|
|
|
R, |
|
|
x10, |
|
|
ϕ20, |
|
x |
|
, |
|
|
ϕ |
20 |
, |
|
x1стат, |
|
|
||||||||||||||||||||
|
|
|
|
кг |
|
кг |
|
кг |
|
|
Нм/рад |
|
Нм/рад |
|
Н/см |
|
|
|
м |
|
|
см |
|
|
рад |
|
10 |
|
|
|
|
|
|
|
|
см |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
см/с |
|
рад/с |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
5 |
|
|
2 |
|
|
1 |
|
|
|
1 104 |
|
|
2 104 |
|
100 |
|
|
|
0,1 |
|
|
0,3 |
|
|
0,01 |
|
0,1 |
|
|
|
|
|
|
0 |
|
|
0,3 |
|
|
|||||||||||||||||||
|
|
2 |
|
4 |
|
|
1,5 |
|
|
2 |
|
|
|
2 104 |
|
|
3 104 |
|
200 |
|
|
|
0,2 |
|
|
0 |
|
|
0 |
|
|
|
0,2 |
|
|
|
|
|
|
0 |
|
|
0,2 |
|
|
|||||||||||||||||
|
|
3 |
|
5 |
|
|
1 |
|
|
1,2 |
|
|
|
3 104 |
|
|
1 104 |
|
150 |
|
|
|
0,3 |
|
|
0,2 |
|
|
0,02 |
|
|
0 |
|
|
|
|
0,1 |
|
|
0,1 |
|
|
||||||||||||||||||||
|
|
4 |
|
4 |
|
|
1,5 |
|
|
1 |
|
|
|
2 104 |
|
|
1 104 |
|
100 |
|
|
|
0,2 |
|
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
0,2 |
|
|
0,3 |
|
|
||||||||||||||||||
|
|
5 |
|
5 |
|
|
1,8 |
|
|
1,2 |
|
2 104 |
|
|
1 104 |
|
100 |
|
|
|
0,1 |
|
|
0,5 |
|
|
0,01 |
|
0,3 |
|
|
|
|
|
|
0 |
|
|
0,2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
Варианты условий для рис. 11, 17, 19, 22 (для рис. 17: m4 = m1) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
№ |
|
m1, |
|
m2, |
|
m3, |
|
|
|
c1, |
|
|
|
|
|
c2, |
|
|
c3, |
|
|
|
R, |
|
|
ϕ10, |
|
|
ϕ20, |
|
ϕ |
|
, |
|
|
ϕ |
20 |
, |
|
ϕ1стат, |
|
|
||||||||||||||||||
|
|
|
|
кг |
|
кг |
|
кг |
|
|
Нм/рад |
|
Нм/рад |
|
Нм/рад |
м |
|
|
рад |
|
|
рад |
|
10 |
|
|
|
|
|
|
|
|
рад |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рад/с |
|
рад/с |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
5 |
|
|
2 |
|
|
1 |
|
|
|
1 104 |
|
|
2 104 |
|
1,5 104 |
0,1 |
|
|
0 |
|
|
|
|
0,01 |
|
0,1 |
|
|
|
|
|
|
0 |
|
|
0,03 |
|
|
||||||||||||||||||||
|
|
2 |
|
4 |
|
|
1,5 |
|
|
2 |
|
|
|
2 104 |
|
|
3 104 |
|
1 104 |
|
|
|
0,2 |
|
|
0,02 |
|
|
0 |
|
|
|
0,15 |
|
|
|
|
|
0 |
|
|
0,02 |
|
|
||||||||||||||||||
|
|
3 |
|
5 |
|
|
1 |
|
|
1,2 |
|
|
|
3 104 |
|
|
1 104 |
|
2 104 |
|
|
|
0,3 |
|
|
0 |
|
|
|
|
0,02 |
|
0 |
|
|
|
|
0,1 |
|
|
0,01 |
|
|
|||||||||||||||||||
|
|
4 |
|
4 |
|
|
1,5 |
|
|
1 |
|
|
|
2 104 |
|
|
1 104 |
|
1 104 |
|
|
|
0,2 |
|
|
0,01 |
|
|
0 |
|
|
|
0 |
|
|
|
|
0,2 |
|
|
0,03 |
|
|
|||||||||||||||||||
|
|
5 |
|
5 |
|
|
1,8 |
|
|
1,2 |
|
2 104 |
|
|
1 104 |
|
1 104 |
|
|
|
0,1 |
|
|
0 |
|
|
|
|
0,01 |
|
0,1 |
|
|
|
|
|
|
0 |
|
|
0,02 |
|
|
|||||||||||||||||||
|
|
|
|
|
Варианты условий для рис. 14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
№ |
|
|
m1, |
m2, |
|
m3, |
|
|
c1, |
|
|
c2, |
|
|
c3, |
|
|
|
R, |
|
|
ϕ10, |
|
|
x20, |
|
ϕ |
|
, |
|
|
|
x |
20 |
, |
|
ϕ1стат, |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
кг |
|
кг |
|
кг |
|
Нм/рад |
|
|
Н/см |
|
Н/см |
|
|
|
м |
|
|
рад |
|
|
см |
10 |
|
|
|
|
|
|
|
рад |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рад/с |
|
|
см/с |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
5 |
|
|
2 |
|
|
1 |
|
|
|
|
3 103 |
|
40 |
|
|
30 |
|
|
|
|
0,1 |
|
0 |
|
|
|
0,3 |
|
|
0,1 |
|
|
|
|
|
0 |
|
|
0,03 |
|
|
||||||||||||||||
|
|
2 |
|
|
4 |
|
|
1,5 |
|
2 |
|
|
|
|
4 103 |
|
30 |
|
|
20 |
|
|
|
|
0,2 |
|
0,02 |
|
|
0 |
|
|
0,15 |
|
|
|
|
|
0 |
|
|
0,02 |
|
|
||||||||||||||||||
|
|
3 |
|
|
5 |
|
|
1 |
|
|
1,2 |
|
|
3 103 |
|
25 |
|
|
30 |
|
|
|
|
0,1 |
|
0 |
|
|
|
0,2 |
|
|
0 |
|
|
|
|
0,1 |
|
|
0,01 |
|
|
|||||||||||||||||||
|
|
4 |
|
|
4 |
|
|
1,5 |
|
1 |
|
|
|
|
2 103 |
|
35 |
|
|
20 |
|
|
|
|
0,2 |
|
0,01 |
|
|
0 |
|
|
0 |
|
|
|
|
0,2 |
|
|
0,03 |
|
|
|||||||||||||||||||
|
|
5 |
|
|
5 |
|
|
1,8 |
|
1,2 |
|
|
2 103 |
|
30 |
|
|
40 |
|
|
|
|
0,1 |
|
0 |
|
|
|
0,5 |
|
|
0,1 |
|
|
|
|
|
0 |
|
|
0,02 |
|
|
|||||||||||||||||||

20
Варианты условий для рис. 30
№ |
m1, кг |
m2, кг |
c1, |
c2, |
c3, |
ϕ10, |
ϕ20, |
ϕ , |
ϕ |
20 |
, |
ϕ1стат, |
|
|
|
Нм/рад |
Н/см |
Н/см |
рад |
рад |
10 |
|
|
рад |
|
|
|
|
рад/с |
рад/с |
||||||||
1 |
30 |
30 |
2 104 |
80 |
100 |
0 |
0,01 |
0,1 |
|
0 |
|
0,03 |
2 |
25 |
25 |
1,5 104 |
100 |
90 |
0,02 |
0 |
0,15 |
|
0 |
|
0,02 |
3 |
30 |
30 |
1,5 104 |
90 |
80 |
0 |
0,02 |
0 |
0,1 |
|
0,01 |
|
4 |
25 |
25 |
2 104 |
90 |
100 |
0,01 |
0 |
0 |
0,2 |
|
0,03 |
|
5 |
30 |
30 |
2 104 |
80 |
90 |
0 |
0,01 |
0,1 |
|
0 |
|
0,02 |
или силы F = F0 sin ωt, приложенных к телу 1 в плоскости его колебаний. Угловое (линейное) смещение тела 1 при M = M0 (F = F0) равно ϕ1стат
(x1стат).
Методические указания и пример решения задачи
Дано: m1 = 40 кг, m2 = 60 кг,
R1 = R; R2 = 1,2R, R = 0,4 м, c1 = 1 104 Н м/рад,
c2 = 3 104 Н м/рад, c = 6 104 Н/м, ϕ10 = 0, ϕ10 = 0,1 рад/с, ϕ20 = 0,01 рад, ϕ20 = 0, ϕ1стат = 0,03 рад.
Необходимо: исследовать свободные и вынужденные колебания систе-
мы.
Рис. 7
Решение.
3.1.Уравнения движения механической системы
Предположим, что в состоянии покоя системы (состоянии равновесия) пружина с коэффициентом жесткости c деформирована на величину λст, а валы с коэффициентами жесткости c1 и c2 закручены на углы ϕст1 и ϕст2 соответственно.
Для решения задачи составим систему уравнений Лагранжа второго рода |
|
||||||||
|
d |
|
∂T |
|
|
∂T |
|
|
|
|
|
|
− |
=Qi , |
i = 1, 2. |
(1) |
|||
|
|
∂q |
∂q |
||||||
|
dt |
|
|||||||
|
|
|
i |
|
i |
|
|
|
|
Так как в задаче рассматриваются малые колебания вблизи положения равновесия консервативной механической системы со стационарными связями, то кинетическая и потенциалная энергии системы записываются в форме
T = |
1 |
T |
€ |
q€= |
1 |
2 |
|
2 |
+ 2m12q1q2 ) , |
|
|
2 q€ |
M |
2 |
(m11q1 |
|
+ m22q2 |
|
|||||
Π = |
1 |
T |
€ |
q€= |
1 |
2 |
|
2 |
+ 2c12q1q2 ) , |
(2) |
|
2 |
q€ |
C |
2 |
(c11q1 |
+ c22q2 |
||||||
|
|
|
|
|
|
|
|
|
|
||
21
€ |
− вектор-столбец |
€ |
− вектор-столбец |
|
где q |
обобщенных координат; q |
|||
|
€ |
|
€ |
− |
обобщенных скоростей; M |
− 2×2 матрица коэффициентов инерции; C |
|||
2×2 матрица обобщенных коэффициентов жесткости. Верхний индекс “Т” означает операцию транспонирования. В уравнениях (2) учтено, что
матрицы € и € являются симметричными, то есть m = m и c = c .
M C 12 21 12 21
Тогда систему уравнений Лагранжа (1) можно записать как систему линей-
ных однородных дифференциальных уравнений движения: |
|
|
€ |
€ |
(3) |
M q€ |
+ C q€= 0 , |
|
или |
|
|
m11q1 + c11q1 + c12q2 = 0 , |
|
|
m22q2 + c21q1 + c22q2 = 0 , |
(4) |
|
€€
исоставление уравнений движения сводится к нахождению матриц M и C . В качестве обобщенных координат выберем: ϕ1 и ϕ2 − углы поворота колес 1
и2 от их равновесных положений соответственно (рис. 7). Сформируем век- тор-столбец обобщенных координат:
|
ϕ |
|
(5) |
q€= |
1 |
. |
|
|
ϕ2 |
|
|
|
|
|
Кинетическая энергия системы состоит из кинетической энергии двух колес:
|
I ϕ2 |
|
I |
2 |
ϕ2 |
|
|
T = |
1 1 |
+ |
|
2 |
. |
(6) |
|
2 |
|
2 |
|||||
|
|
|
|
|
|||
Сравнивая соотношения (2) и (6) для кинетической энергии системы, легко получить выражение для матрицы коэффициентов инерции:
€ |
m |
m |
|
I |
1 |
0 |
|
|
0,5m R |
2 |
0 |
|
|
|
3,2 |
0 |
|
|
||
|
11 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
M |
= |
|
|
|
= |
|
|
|
= |
|
|
|
|
2 |
|
= |
|
|
. |
(7) |
|
|
|
|
|
|
0 |
|
|
0 |
|
0,72m2 R |
|
0 |
6,912 |
|
|
||||
|
m21 |
m22 |
|
I2 |
|
|
|
|
|
|
|
|
||||||||
В данном случае были учтены явные выражения для моментов инерции I1 и I2 колес, представляемых однородными дисками.
Если механическая система имеет более сложную структуру, следует воспользоваться кинематическими соотношениями, выразить ее кинетическую энергию через обобщенные скорости и привести к виду (6), что позволит найти приведенные моменты инерции или массы.
Потенциальную энергию системы вычислим как сумму
Π = Πтяж + Πупр,
где Πтяж — потенциальная энергия тел в поле сил тяжести; Πупр потенциальная энергия деформированных валов и пружины.
Так как при движении системы положение центров масс колес не изменяет-
ся, то принимаем Πтяж = 0.
Потенциальную энергию пружин и валов найдем, выбрав в качестве нулевого значение потенциальной энергии системы в положении покоя
22
Πравн = 12 c1ϕст2 1 + 12 c2ϕст2 2 + 12 cλ2ст . |
|
|
|
|
|
|
|
(9) |
|||||||
Тогда потенциальная энергия системы принимает вид |
|
|
|
|
|
|
|||||||||
Π = 1 c (ϕ + ϕ |
ст1 |
)2 + 1 c |
2 |
(ϕ |
2 |
+ ϕ |
ст2 |
)2 + 1 c(ϕ R + ϕ |
R + λ |
ст |
)2 |
− Π |
равн |
= |
|
2 1 1 |
2 |
|
|
2 |
1 1 |
2 2 |
|
|
|
||||||
=12 c1ϕ12 + 12 c2ϕ22 + 12 c(ϕ1R1 + ϕ2 R2 )2 +
+c1ϕст1ϕ1 + c2ϕст2ϕ2 + cλст(ϕ1R1 + ϕ2 R2 ).
Сучетом условий равновесия рассматриваемой системы, находящейся под действием потенциальных сил,
|
∂Π |
|
|
|
|
|
|
|
|
|
|
∂Π |
|
|
|
|
|
|
|
|
|
|
ϕ =0 = (c1ϕст1 |
+ cλстR1) = 0 , |
|
|
|
|
|
ϕ =0 = (c2ϕст2 + cλстR2 ) = 0 , |
|||||||||
∂ϕ |
∂ϕ |
|
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||
|
1 |
|
ϕ12 =0 |
|
|
|
|
|
|
|
|
2 |
|
|
ϕ12 =0 |
|
|||
перепишем потенциальную энергию в виде |
|
|
|
|
|
|
|
||||||||||||
Π = 1 (c |
+ cR2 )ϕ2 + |
1 |
(c |
2 |
+ cR2 )ϕ2 |
+ cR R ϕ ϕ |
2 |
. |
(10) |
||||||||||
|
2 |
1 |
1 |
1 |
2 |
|
2 |
2 |
1 |
2 |
|
1 |
|
|
|
||||
Отметим, что в данном случае система двух уравнений равновесия включает три неизвестные статические деформации ϕст1, ϕст2 , λст, и, следовательно,
имеет бесчисленное множество решений. Одно из них соответствует случаю, когда в состоянии равновесия ни один из упругих элементов не напряжен и все статические деформации равны нулю. Если задать предварительный натяг одного из упругих элементов, уравнения равновесия позволяют найти значения статических деформаций двух остальных.
Сравнивая соотношения (2) и (10) для потенциальной энергии системы, получаем выражение для матрицы обобщенных коэффициентов жесткости:
€ |
|
|
|
|
|
2 |
|
|
cR1R2 |
|
|
1,96 |
|
1,152 |
|
|
4 |
|
|
||||||||
|
c1 |
+ cR1 |
|
|
|
|
|
10 |
Н м/(рад с). |
(11) |
|||||||||||||||||
C |
= |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
cR R |
|
c |
|
|
+ cR2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
1,152 |
|
4,3824 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
€ |
€ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в уравнения движения системы (3) и |
||||||
Подставим найденные матрицы C и M |
|||||||||||||||||||||||||||
получим систему двух дифференциальных уравнений движения системы |
|||||||||||||||||||||||||||
m ϕ + |
(c + cR2 )ϕ + cR R ϕ |
2 |
= 0, |
|
|
|
|
(12а) |
|||||||||||||||||||
m |
11 |
1 |
|
1 |
|
1 |
|
1 |
|
|
1 |
2 |
|
|
= |
0 |
|
|
|
|
|||||||
22 |
ϕ |
2 |
+ cR R ϕ + (c |
2 |
+ cR2 )ϕ |
2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
1 |
2 |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
или после деления первого уравнения на m11, а второго − на m22 |
|
||||||||||||||||||||||||||
ϕ1 |
+ a11ϕ1 |
+ a12ϕ2 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
(12б) |
|||||||||||
ϕ2 |
+ a21ϕ1 |
+ a22ϕ2 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
где элементы матрицы |
€ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
€ |
|
a11 |
a12 |
|
= |
|
6125 |
|
3600 |
|
|
|
|
|
|
|
|
|
(13) |
||||||||
A |
= |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
a22 |
|
|
|
|
|
|
|
6340 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
a21 |
|
|
|
1667 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Здесь деление на m11 и m22 выполнено с целью упрощения последующих вычислений. Этого можно не делать и все вычисления выполнить для уравнений движения в форме (12а).

23
3.2.Частоты свободных колебаний механической системы
Для определения частот свободных колебаний составим характеристическое уравнение, соответствующее уравнениям движения (12б). С этой целью будем искать общее решение указанных уравнений в виде
ϕ1 = α1 sin(kt + δ) , ϕ2 = α2 sin(kt + δ) , (14)
где α1 и α2 − амплитуды изменений обобщенных координат; δ − начальная фаза колебаний; k − собственная частота колебаний системы. После подста-
новки (14) в (12б) и сокращения на sin(kt + δ) |
получаем для системы с дву- |
||||||||
мя степенями свободы |
|
||||||||
(a |
− k 2 )α |
+ a |
|
α |
2 |
= 0 , |
(15а) |
||
11 |
|
1 |
12 |
|
|
|
|||
a α + (a |
22 |
− k |
2 )α |
2 |
= 0 . |
(15б) |
|||
21 |
1 |
|
|
|
|
|
|
||
Чтобы полученная система уравнений для амплитуд α1 и α2 имела нетривиальное решение (не все амплитуды равны нулю), ее определитель должен быть равен нулю, что приводит к характеристическому уравнению
a − k 2 |
a |
= 0 , |
11 |
12 |
|
a21 |
a22 − k 2 |
|
которое после раскрытия определителя принимает вид биквадратного уравнения относительно k:
k 4 −(a |
+a |
22 |
)k 2 + a a |
22 |
−a a |
21 |
= 0 . |
(16) |
11 |
|
11 |
12 |
|
|
Это биквадратное уравнение после подстановки числовых значений имеет вид
(k 2 )2 −12465,3k 2 + 32834200 = 0 .
Решая это уравнение, находим спектр собственных частот рассматриваемой механической системы:
k1 = 61,5 рад/с, k2 = 93,2 рад/с. (17)
3.3.Формы главных колебаний системы
Двум частотам свободных колебаний соответствуют два линейно независимых решения системы дифференциальных уравнений (13):
ϕ(1) |
= α(1) sin(k t + δ ) , |
ϕ(1) |
= α(1) sin(k t + δ ) |
|
(18а) |
|||||||||
1 |
1 |
1 |
1 |
|
|
2 |
2 |
1 |
1 |
|
|
|
||
ϕ(2) |
= α(2) sin(k |
2 |
t + δ |
2 |
) , |
ϕ(2) |
= α(2) sin(k |
2 |
t + δ |
2 |
) . |
(18б) |
||
1 |
1 |
|
|
|
2 |
2 |
|
|
|
|
||||
Здесь уравнения (18а) представляют собой первую форму колебаний, а (18б) − вторую. Уравнения (15а) и (15б), которые при k = k1 и k = k2 тождествен-
ны друг другу, позволяют записать соотношения между амплитудами обобщенных координат
α(1) |
= − |
a11 − k12 |
α(1) |
= − |
|
a21 |
α(1) |
, |
(19а) |
|
a12 |
a |
|
||||||||
2 |
|
1 |
|
22 |
− k 2 |
1 |
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
