
pechat_33
.pdf
10.Единственность и устойчивость решения задачи Коши для волнового уравнения.
(1)
Теорема. Задача Коши для волнового уравнения имеет не более одного решения.
Док-во. Допустим противное. Пусть
|
различные решения (1).Обозначим |
|
их разность через |
. Тогда |
решение задачи: |
|
|
(2). Очевидно, что задача |
(2) имеет нулевое решение. Нам нужно показать, что других решений эта задача не имеет. В пр-ве  возьмем т.
возьмем т.
и через нее как через вершину проведем конус
.
Воспользуемся тождеством:
Проинтегрируем это тождество по объему усеченного конуса . Тогда
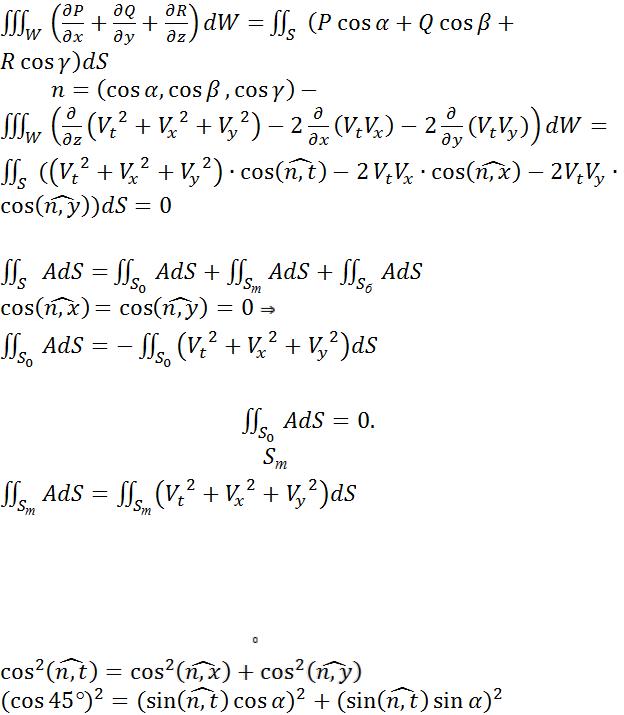
Если функция 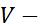 решение задачи (2), то в левой части последнего равенства подынтегральное выражение равно нулю,
решение задачи (2), то в левой части последнего равенства подынтегральное выражение равно нулю, сумма интегралов, стоящих в правой части обращается в нуль.
сумма интегралов, стоящих в правой части обращается в нуль.
, где |
вектор нормали. Тогда |
.Но на нижнем основании согласно нач. условиям (2):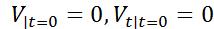
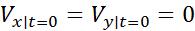 и
и 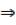 Рассмотрим поверхность :
Рассмотрим поверхность :
(3)
На боковой поверхности направляющие косинусы вектора нормали удовлетворяют соотношению: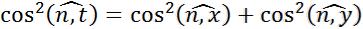
Образующие усеченного конуса наклонены к плоскости основания под углом 45 .
(4)
С учетом равенства (4) преобразуем выражение стоящее под знаком интеграла по боковой поверхности:

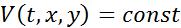 .Но
.Но 
Покажем, что решение задачи Коши
устойчиво, т.е.
Обозначим через |
. Тогда |
решение задачи: |
|
|
(5) |
11.Элементарное (фундаментальное) решение уравнения теплопроводности.
Рассмотрим сначала одномерное уравнение теплопроводности Ut a2U xx . Среди всех решений свёртка этого решения с единицей должна давать единицу, т.е.
E(t, )d 1.Воспользуемся преобразованием Фурье, и
|
|
|
|
|
|
|
|
|
|
|
будем искать решение E(t, x) V (t, y)eixy dy .Найдём его: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
e |
x2 |
|
Et (t, x) Vt (t, y)eitxdy |
И |
E(t, x) |
|
|
|
|
4a2t |
– |
||
2a |
|
|
|
|
||||||
|
|
|
|
|||||||
|
|
|
|
t |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
фундаментальное решение уравнения теплопроводности. Заметим, что чаще используется не это решение, а функция
|
|
1 |
|
|
|
|
( x )2 |
|
E(t, x ) |
|
|
|
|
e |
4a2t |
|
|
|
|
|
|
|
, которая называется функцией |
|||
|
2a |
|
t |
|
||||
|
|
|
|
|||||
Грина (функцией источника).
Определим теперь фундаментальное решение уравнение теплопроводности в случае произвольного числа
n |
2 |
пространственных решение, т.е. Ut a2 U , U U2 . |
|
i 1 |
x |
i |
|
Рассмотрим уравнение Ut a2 (Uxx Uyy ) . Покажем, что функция E(t, x, y) E(t, x)E(t, y) является фундаментальным решением этого уравнения и покажем,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что |
E(t, , )d d 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x2 |
|
1 |
|
|
|
y2 |
|
|
1 |
2 |
|
x2 y2 |
|
||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
||||||||||||
E(t, x, y) |
|
|
|
|
e |
4a |
t |
|
|
|
|
e |
4a |
t |
|
|
|
|
|
|
e |
4a |
t |
– |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2a |
t |
|
|
|
2a t |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2a |
t |
|
|
|
|
|
|||||||||
фундаментальное решение для двух пространственных переменных.
|
|
1 |
|
|
|
|
( x )2 |
( y )2 |
|
|
E(t, x , y ) |
|
2 e |
4a2t |
. |
||||||
|
|
|||||||||
|
|
|
|
) |
|
|
|
|
|
|
|
(2a |
|
t |
|
|
|
|
|
|
|

12.Задача Коши для уравнения теплопроводности. Формула Пуассона.
Ut
Пусть имеем задачу U
a2 U f (t, x) |
t 0 |
|
|
|
(x) |
x |
(1) |
t 0 |
|
||
|
|
|
|
Решение задачи (1) есть сумма решения двух задач:
|
U a |
U |
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
Ut |
|
2 |
U f (t, x) |
|
|
|
t |
|
|
|
|
a |
|
|||||
UО |
: |
|
|
(x) (2) |
UН |
: |
|
|
|
0 |
(3) |
|
|
|
|
|
|||||||||
|
U |
|
|
|
U |
|
|
|||||
|
|
|
t 0 |
|
|
|
|
|
t 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение задачи (2) есть свёртка начального условия и соответствующей функции источника (функции Грина).
|
|
|
|
|
1 |
|
|
e |
|
x |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
UО |
( )E(t, x )d |
... ( 1,..., n )E(t, x1 1,..., xn n )d 1...d n |
|
|
|
|
|
4a2t |
|||||||
|
|
|
|
n |
|||||||||||
(2a |
|
t ) |
|
|
|
|
|
||||||||
n |
|
|
|
|
|
n |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
-формула Пуассона.Покажем, что UО удовлетворяет уравнению задачи (2) и для него выполняется начальное условие этой задачи.
( )d
Uоt ( )Et (t, x )d |
Uо ( ) E(t, x )d |
n |
n |
( )[Et (t, x ) a2 E(t, x )]d 0
n
Начальное условие выполняется формула Пуассона остаётся верной.
Для решения задачи (3) воспользуемся принципом Дюамеля, согласно которому, если V (t, , x) – решение
|
|
|
|
|
V |
|
|
a2 |
V |
|
|
|
||
|
|
|
|
|
tt |
|
|
|
(4) x |
n . То |
||||
вспомогательной задачи |
|
|
|
|
f ( , x) |
|||||||||
|
|
|
||||||||||||
|
|
|
|
|
V |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
t 0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
решение задачи (3) определяется формулой |
|
|
||||||||||||
|
t |
|
|
|
|
t |
V (t, , x)d V (t,t, x) |
|
|
|||||
UН (t, x) |
|
V (t, , x)d |
(5). |
U |
|
; |
|
|||||||
|
|
|
Нt |
|
t |
|
|
|
||||||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
t
UН V (t, , x)d . Если подставить решение задачи (3)
0
получим:
t |
V |
|
|
|
|
t |
a2 V d f (t, x) f (t, x) . Функция U |
удовлетворяет |
|
0 |
|
|
|
|
0
решению уравнения (3). И решение (3) UН t 0 Vd 0 .
0
Для нахождения функции V (t, , x) во вспомогательной
задаче сделаем замену S t .
задачи Коши можно определить
|
|
1 |
|
|
f ( , )e |
|
x |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
V |
|
|
|
|
4a2S dS [S t |
||||||||
|
|
|
|
n |
|||||||||
2a |
|
S |
|||||||||||
|
|
|
n |
|
|
|
|
|
|
||||
V V |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
V |
|
|
f ( , x) |
(6). Решение |
|||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
с помощью формулы: |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
|
|
|
x |
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
] |
|
|
|
|
|
|
|
f ( , x)e 4a |
(t ) d |
||||||||
|
|
|
|
|
|
n |
|||||||||||
|
2a |
(t ) |
|||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||
13.Принцип экстремума для уравнений теплопроводности.
При рассмотрении процесса распространения тепла в областях, ограниченных необходимо учитывать не только начальное распределение температуры, но и те процессы, которые происходят на границе этой области. Границу области в пространстве любой размерности будем обозначать через Γ, а саму область Ω. В
зависимости от задания условий на границе различают три типа граничных (смешанных) задач.
1) |
U |
|
Г |
g(t, x) – первая граничная задача. |
|
|
||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
2) |
U |
|
|
|
|
|
U |
– |
||
n |
|
|
g(t, x) – вторая граничная задача. Где |
|
||||||
|
|
|
Г |
|
|
n |
|
|||
|
|
|
||||||||
нормаль в точках границы. |
|
|
||||||||
3) |
U |
|
|
g(t, x) – третья краевая задача. |
|
|
||||
|
|
|
||||||||
|
|
|
|
|
U |
|
|
|
||
|
n |
|
|
Г |
|
|
||||
|
|
|
|
|||||||
|
U |
t |
a2 U f (t, x) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
(x) |
|
|
|
|
Рассмотрим задачу: |
U |
|
t 0 |
, где x |
n |
. |
||
|
|
|
|
|||||
|
|
|
|
|
|
|
||
|
U |
|
|
g(t, x) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
||
Обозначим через |
Q R |
, |
R [0;T ] |
. |
T |
|
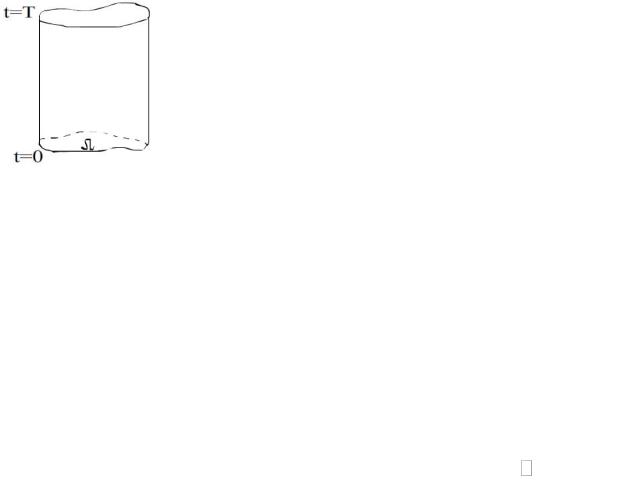
Принцип: Функция U (t, x) удовлетворяющая уравнению
Ut a2 U в цилиндре и непрерывна вплоть до его границы QT принимает своё наибольшее и наименьшее значение либо на нижнем основании цилиндра (область Ω ), либо на его боковой поверхности.
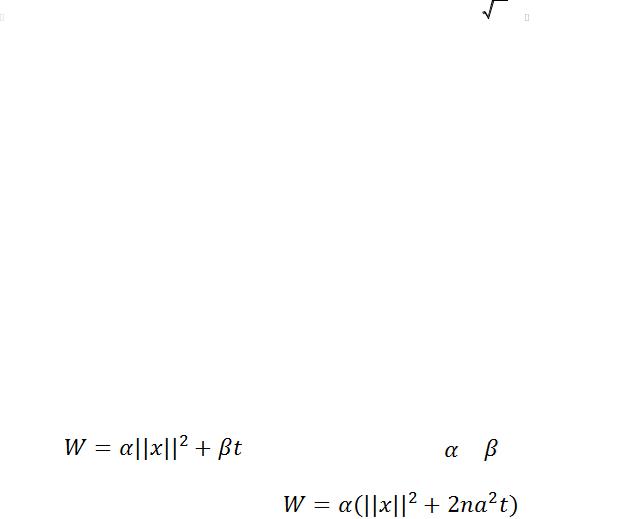
14.Единственность и устойчивость решения задачи Коши для уравнения теплопроводности.
Утверждение: Задача Коши для уравнения теплороводности не может иметь более одного ограниченного решения.
U |
t |
a2 U f (t, x) |
|
|
|
|
|
|
|
Пусть имеем задачу |
|
|
(x) |
(1) |
|
|
|||
U |
|
|
|
|
|
|
t 0 |
|
|
|
|
|
||
Решение задачи (1) есть сумма решения двух задач:
|
U |
t |
a2 |
U |
|
|
|
|
|
|
|
|
|
UО |
: |
|
|
(x) |
(2) |
|
|
|
|||||
|
U |
|
|
|
||
|
|
|
t 0 |
|
|
|
|
|
|
|
|
||
|
U |
t |
a2 U f (t, x) |
|
||
|
|
|
|
|
|
|
UН |
: |
|
|
|
0 |
(3) |
|
|
|||||
|
U |
|
|
|
||
|
|
|
t 0 |
|
|
|
|
|
|
|
|
||
Решение задачи (2) есть свёртка начального условия и соответствующей функции источника (функции Грина).
|
|
|
|
|
1 |
|
|
e |
|
x |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
UО |
( )E(t, x )d |
... ( 1,..., n )E(t, x1 1,..., xn n )d 1...d n |
|
|
|
|
|
4a2t ( )d |
||||||||
|
|
|
|
n |
||||||||||||
(2a |
|
t ) |
||||||||||||||
n |
|
|
|
|
|
n |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теорема: Решение задачи Коши устойчиво т.е. малое изменения начальных условий влечёт за собой малое изменение решений.
Единственность решения задачи Коши для уравнения теплопроводности.
U |
a2 U f (t, x) |
(t,x)=[0,T]×Ω Rn |
Рассмотрим задачу t |
|
|
U |t 0 (x) |
|
|
Эта задача имеет бесконечное множество решений. Рассмотрит подмножество решений, будем рассматривать |V(t,x)| M (т.е. будем рассматривать ограниченные
|
|
V a2 |
U |
|
решения). |
Рассмотрим задачу |
t |
|
(2).Задача |
|
|
V |t 0 |
0 |
|
(2) имеет нулевое решение. Докажем, что других решений нет. Для этого рассмотрим вспомогательную
функцию: |
и подберём теперь и |
таким |
образом, чтобы ф-я W удовлетворяла однородному |
|
|
уравнению теплопроводности: |
. |
|

Теорема:Задача Коши имеет не более одного ограниченного решения.
16. *Формулы Грина. Формулы Грина для оператора
Лапласа
При изучении решения смешанных задач мы ввели в
рассмотрение линейный оператор: L[U ] div(kgradU) qU. При доказательстве самосопряженности этого оператора была получена первая формула Грина:
Меняя местами функции U и V запишем еще одну формулу:
Вторая формула Грина:
.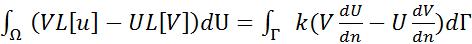 U=V: Третья формула Грина
U=V: Третья формула Грина
L[U ] div(k, gradU ) qAU . k(x)=1, q=0
L[U ] div(gradU) div( U ,..., U ) U
x1 xn
Формулы Грина для оператора Лапласа 1 рода
