
Инф. безопасность
.pdfSAUNA AND HEALTH. Так как шифруемые блоки состоят из 10 разрядов, то делениенаблокинашегоисходноготекстадаст:
SA UN АпробелAN DпробелНЕAL ТН Соответствующие8 двоичныхпоследовательностей:
1001100001 ,
1010101110 ,
0000100000 ,
0000101110 , 0010000000, 0100000101 , 0000101100 , 1010001000 .
являются аргументами значений рассмотренной выше функции, следовательно, криптотекстомбудетнабор
(2942, 3584, 903, 3326, 215, 2817, 2629, 819) .
Определенная таким образом на основе функции рюкзака f(x) криптосистема еще не является системой с открытым ключом. Действительно, мы можем использовать ее как классическую систему. Тогда криптоаналитик находит n-набор А и после этого решает еще и задачуорюкзаке.
Если криптоаналитик может использовать в качестве условия анализа «избранный исходный текст», то криптоаналитик использует исходные сообщения с ровно одним появлением единицы и легко находит вектор А.
Но для расшифрования легальный получатель также должен решать задачу о рюкзаке. Это означает, что расшифрование одинаково трудно и для криптоаналитика, и для легального получателя. Такая ситуация нежелательна: она показывает, что криптосистема очень несовершенна. В хороших криптосистемах расшифрование значительно труднее для криптоаналитика, чем для легального получателя.
Прежде чем улучшить данную криптосистему и преобразовать ее в систему с открытым ключом, сделаем один вывод. Никогда нельзя получить два различных исходных сообщения из одного и того же криптотекста. Это означает, что не существует двух равных сумм, по-разному сформированных из элементов набора А. Суммы могут иметь одинаковое или разное число слагаемых, но каждый элемент из А может быть
51
использован только один раз.
Теперь преобразуем криптосистему, основанную на n- наборе А, в систему с открытым ключом. Сначала сделаем несколько замечаний, а затем вернемся к нашей числовой иллюстрации.
Существуют подклассы легких задач укладки рюкзака. Один из них получается из сверхрастущих n-наборов А. n-Набор
A= (a1, a2,...,an)
называется сверхрастущим, если каждое следующее число в нем большесуммывсехпредыдущих, т.е.
j−1
a j > ∑ai для j = 2,..., n
i=1
Нет необходимости в полном переборе при решении соответствующей задачи о рюкзаке — достаточно просмотреть А один раз справо налево. Для заданного k (размера рюкзака) мы сначала проверяем k ≥ а. Если ответом будет «нет», аn не может входить в искомую сумму. Если же ответом будет «да», то аn должно входить в сумму. Это следует из того факта, что все оставшиеся аi -e в сумме дают число, меньшее k. Определим,
k1 |
k, |
если k < an , |
= |
= k − an , если k ≥ a |
|
|
k |
и повторим ту же самую процедуру для k1 и аn-1 . Так можно дойти до а1. Алгоритм также показывает, что для любого k задача рюкзака имеет не более одного решения, при условии, что А является сверхрастущим.
Если мы раскрываем сверхрастущий набор А как основу криптосистемы, то расшифрование будет одинаково легким для криптоаналитика и легального получателя. Чтобы избежать этого, мы «взболтаем» А таким образом, чтобы результирующий набор В не являлся сверхрастущим и выглядел как произвольный вектор рюкзака. В действительности он только выглядит как произвольный, потому что очень немногие векторы рюкзака могут быть получены таким способом: используемое нами взбалтывание является модульным умножением.
Выберем целое m > ∑ai . Так как А сверхрастущий, то m
велико по сравнению со всеми числами из А. Выберем другое целое t, не имеющее общих множетелёй c m. m и t являются
52
модулем и множителем. Такой выбор t гарантирует, что найдется другое целое t-1, такое, что tt −1 ≡1(mod m). Целое t-1 можно назвать обратным к t. Обратный элемент сможет быть легко вычислен по m
и t.
Теперь образуем произведения tai , i =1,..., n , и сведем их по
модулю m: пусть bi — наименьший положительный остаток tai по модулю m. Результирующий вектор
В = (b1, b2, ... ,bn„)
открывается как ключ зашифрования. Алгоритм зашифрования для n-разрядных блоков исходного сообщения описан выше.
Числа t, t-1 и m хранятся как секретная лазейка. Перед сравнением ситуации с точки зрения криптоаналитика и легального получателя вернемся к уже рассмотренному примеру.
Легко видеть, что наш предыдущий набор (обозначенный теперь через В)
В = (43, 129, 215, 473, 903, 302, 561, 1165, 697, 1523)
получается с помощью модульного умножения с m = 1590 и t = 43 из сверхрастущего вектора рюкзака
А = (1, 3, 5, 11, 21, 44, 87, 175, 349, 701) .
Проверим это более подробно.
Первые пять чисел в В получаются из соответствующих чисел в А простым умножением на 43 — сведение по модулю не нужно. (В реальных ситуациях даже первые числа не должны быть очень маленькими, иначе легко обнаружить множитель.) Следующие вычисления позволяют получить оставшиеся пять чисел в В.
43·44 = 1892 = 1590 + 302, 43·87 = 3741=2·1590 + 561 , 43·175= 7525=4·1590 + 1165 , 43·349=15007=9·1590 + 697 , 43·701=30143=18·1590 +1523 .
Заметим далее, что t и m взаимно просты. Действительно, 43·37= 1591 ≡ 1 (mod 1590) .
Следовательно, t-1 = 37.
Теперь отыщем легкий алгоритм расшифрования для легального получателя. Рассмотрим сначала основной случай, где А является сверхрастущим вектором, а В получается из А
53
умножением каждого числа в A на t (mod m). Так как легальный получатель знает t-1 и m, он в состоянии найти А из открытого ключа В. После получения блока с' криптотекста легальный получатель вычисляет t-1c' и его наименьший положительный остаток с (mod m). При расшифровании он решает легкую задачу укладки рюкзака, определяемую A и с. Решением является единственная последовательность р из n битов. Оно также является и правильным блоком исходного сообщения, так как любое решение р' задачи укладки рюкзака, определяемой В и с', должно равняться р. Действительно,
c ≡ t −1c' = t −1 B p' ≡ t −1 A p' ≡ A p' (mod m).
Отметим, что Ар' < m, так как m > a1 + a2 + ...+an. Это означает, что указанное выше сравнение может быть переписано в виде уравнения с == Ар', Так как задача укладки рюкзака, определяемая А и с не может иметь несколько решений,то_р’=р.
Итак, каким образом легальный получатель может вручную расшифровать криптотекст
(2942, 3584, 903, 3326, 215, 2817, 2629, 819)
полученный ранее? Умножая на t-1 = 37, он/она получает первое число
37·2942 = 108854 = 68·1590+734 ≡ 734 (mod 1590).
Произведя аналогичные вычисления, он получает восьмерку
(734, 638, 21, 632, 5, 879, 283, 93).
Число 734 и сверхрастущий набор А дают. 10-разрядную последовательность 1001100001. Действительно, так как 734 > 701, то последний бит должен быть равен 1. Числа из А теперь сравниваются с разностью 734 - 701 = 33. Первое число, справа налево, меньшее чем 33, есть 21. Следующее число 11 меньше разности 33 — 21 = 12. Наконец, первое число 1 равно разности 12 — 11. Позиции 1, 11, 21 и 701 в А есть соответственно 1, 4, 5 и 10.
Таким же образом числа 638, ..., 93 дают другие семь 10разрядных вышеупомянутых последовательностей. Декодируя все восемь последовательностей, легальный получатель вычисляет исходное сообщение SAUNA AND HEALTH.
5.1Упражнения
1.Получить исходный текст с использованием латинского
54
алфавита из криптотекста: (674, 2421, 1181). Открытый ключ найти, решая легкую задачу укладки ранца на основе сверхрастущего набора и закрытого ключа t-1=43, m=2020.
2.Получить исходный текст с использованием латинского алфавита из криптотекста: (2277, 2617, 4737). Открытый
ключ найти, решая легкую задачу укладки ранца на основе сверхрастущего набора и закрытого ключа t-1=49, m=1910.
3.Получить исходный текст с использованием кириллицы из криптотекста: (7608, 9622, 9710) Открытый ключ найти,
решая легкую задачу укладки ранца на основе сверхрастущего набора и закрытого ключа t-1=53, m=4610.
6Общие сведения об асимметричных криптоалгоритмах
Симметричные криптосистемы обладают одним серьезным недостатком. Связан он с ситуацией, когда общение между собой производят не три-четыре человека, а сотни и тысячи людей. В этом случае для каждой пары, переписывающейся между собой, необходимо создавать свой секретный симметричный ключ. Это в итоге приводит к существованию в системе из N пользователей N2/2 ключей. А это уже очень «приличное» число. Кроме того, при нарушении конфиденциальности какой-либо рабочей станции злоумышленник получает доступ ко всем ключам этого пользователя и может отправлять, якобы от его имени, сообщения всем абонентам, с которыми «жертва» вела переписку.
Своеобразным решением этой проблемы явилось появление асимметричной криптографии. Эта область криптографии очень молода по сравнению с другими представителями. Первая схема, имевшая прикладную значимость, была предложена всего около 20 лет назад. Но за это время асимметричная криптография превратилась в одно из основных направлений криптологии, и используется в современном мире также часто, как и симметричные схемы.
Асимметричная криптография изначально задумана как средство передачи сообщений от одного объекта к другому (а не для конфиденциального хранения информации, которое обеспечивают только симметричные алгоритмы). Поэтому
55
дальнейшее объяснение мы будем вести в терминах «отправитель» – лицо, шифруюшее, а затем отпраляющее информацию по незащищенному каналу и «получатель» – лицо, принимающее и восстанавливающее информацию в ее исходном виде. Основная идея асимметричных криптоалгоритмов состоит в том, что для шифрования сообщения используется один ключ, а при дешифровании – другой. [6]
Кроме того, процедура шифрования выбрана так, что она необратима даже по известному ключу шифрования – это второе необходимое условие асимметричной криптографии. То есть, зная ключ шифрования и зашифрованный текст, невозможно восстановить исходное сообщение – прочесть его можно только с помощью второго ключа – ключа дешифрования. А раз так, то ключ шифрования для отправки писем какому-либо лицу можно вообще не скрывать – зная его все равно невозможно прочесть зашифрованное сообщение. Поэтому, ключ шифрования называют в асимметричных системах «открытым ключом», а вот ключ дешифрования получателю сообщений необходимо держать в секрете – он называется «закрытым ключом».
В целом система переписки при использовании асимметричного шифрования выглядит следующим образом. Для каждого из N абонентов, ведущих переписку, выбрана своя пара ключей: «открытый» Ej и «закрытый» Dj, где j – номер абонента. Все открытые ключи известны всем пользователям сети, каждый закрытый ключ, наоборот, хранится только у того абонента, которому он принадлежит.
Как мы видим, во-первых, в асимметричных системах количество существующих ключей связано с количеством абонентов линейно (в системе из N пользователей используются 2*N ключей), а не квадратично, как в симметричных системах. Во-вторых, при нарушении конфиденциальности k-ой рабочей станции злоумышленник узнает только ключ Dk: это позволяет ему читать все сообщения, приходящие абоненту k, но не позволяет выдавать себя за него при отправке писем. (рисунок
11)
56
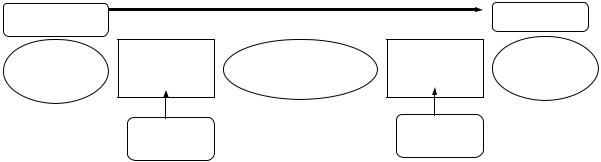
Отправитель |
|
|
|
Адресат |
исходный |
Система |
шифрованный |
Система |
исходный |
с открытым |
с открытым |
|||
текст |
ключом |
текст |
ключом |
текст |
|
Открытый |
|
Закрытый |
|
|
ключ |
|
ключ |
|
Рисунок 11 — Криптографическая система с открытым ключом
Криптографические системы с открытым ключом используют так называемые необратимые или односторонние функции, которые обладают следующим свойством: при заданном значении x относительно просто вычислить значение f(x), однако если y=f(x), то нет простого пути для вычисления значения x.
Чтобы гарантировать надежную защиту информации, к системам с открытым ключом предъявляются два важных и очевидных требования:
1.Преобразование исходного текста должно быть необратимым и исключать его восстановление на основе открытого ключа.
2.Определение закрытого ключа на основе открытого также должно быть невозможным на современном
технологическом уровне.
Вообще же все предлагаемые сегодня криптосистемы с открытым ключом опираются на один из следующих типов необратимых преобразований:
9Разложение больших чисел на простые множители.
9Вычисление логарифма в конечном поле.
9Вычисление корней алгебраических уравнений.
Здесь же следует отметить, что алгоритмы криптосистемы с открытым ключом можно использовать в трех назначениях.
1.Как самостоятельные средства защиты передаваемых и хранимых данных.
2.Как средства для распределения ключей. Алгоритмы более трудоемки, чем традиционные криптосистемы. Поэтому часто на практике рационально с помощью распределять
57
ключи, объем которых как информации незначителен. А потом с помощью обычных алгоритмов осуществлять обмен большими информационными потоками.
3.Средства аутентификации пользователей.
6.1Алгоритм RSA
Алгоритм RSA стоит у истоков асимметричной криптографии. Он был предложен тремя исседователямиматематиками Рональдом Ривестом (R.Rivest), Ади Шамиром
(A.Shamir) и Леонардом Адльманом (L.Adleman) в 1977-1978
годах. [7] Первым этапом любого асимметричного алгоритма является
создание пары ключей: открытого и закрытого и распространение открытого ключа «по всему миру». Для алгоритма RSA этап создания ключей состоит из следующих операций:
1.Выбираются два простых числа p и q
2.Вычисляется их произведение n = p*q
3.Выбирается произвольное число e (e<n), такое, что НОД(e,(p-1)(q-1)) = 1, то есть e должно быть взаимно простым с числом (p-1)(q-1).
4.Методом Евклида решается в целых числах уравнение e*d+(p-1)(q-1)*y=1. Здесь неизвестными являются переменные d и y – метод Евклида как раз и находит множество пар (d,y), каждая из которых является решением уравнения в целых числах.
5.Два числа (e,n) – публикуются как открытый ключ.
6.Число d хранится в строжайшем секрете – это и есть закрытый ключ, который позволит читать все послания,
зашифрованные с помощью пары чисел (e,n).
Как же производится собственно шифрование с помощью этих чисел?
Отправитель разбивает свое сообщение на блоки, равные k=[log2(n)] бит, где квадратные скобки обозначают взятие целой части от дробного числа.
Подобный блок, как Вы знаете, может быть интерпретирован как число из диапазона (0;2k-1). Для каждого такого числа (назовем его mi) вычисляется выражение
58
ci=((mi)e)mod n. Блоки ci и есть зашифрованное сообщение Их можно спокойно передавать по открытому каналу, поскольку операция возведения в степень по модулю простого числа, является необратимой математической задачей. Обратная ей задача носит название «логарифмирование в конечном поле» и является на несколько порядков более сложной задачей. То есть даже если злоумышленник знает числа e и n, то по ci прочесть исходные сообщения mi он не может никак, кроме как полным перебором mi.
А вот на приемной стороне процесс дешифрования все же возможен, и поможет нам в этом хранимое в секрете число d. Достаточно давно была доказана теорема Эйлера, частный случай которой утверждает, что если число n представимо в виде двух
простых чисел p и q, то для любого x имеет место равенство (x(p- 1)(q-1))mod n = 1.
Для дешифрования RSA-сообщений воспользуемся этой формулой. Возведем обе ее части в степень (-y): (x(-y)(p-1)(q-1))mod n
=1(-y) = 1. Теперь умножим обе ее части на x: (x(-y)(p-1)(q-1)+1)mod n
=1*x = x.
Атеперь вспомним как мы создавали открытый и закрытый ключи. Мы подбирали с помощью алгоритма Евклида d такое,
что e*d+(p-1)(q-1)*y=1, то есть e*d=(-y)(p-1)(q-1)+1. А
следовательно, в последнем выражении предыдущего абзаца мы
можем заменить показатель степени на число (e*d). Получаем (xe*d)mod n = x. То есть для того чтобы прочесть сообщение
ci=((mi)e)mod n достаточно возвести его в степень d по модулю m: ((ci)d)mod n = ((mi)e*d)mod n = mi.
На самом деле операции возведения в степень больших чисел достаточно трудоемки для современных процессоров, даже если они производятся по оптимизированным по времени алгоритмам. Поэтому обычно весь текст сообщения кодируется обычным блочным шифром (намного более быстрым), но с использованием ключа сеанса, а вот сам ключ сеанса шифруется как раз асимметричным алгоритмом с помощью открытого ключа получателя и помещается в начало файла.
Пример 17. Зашифруем сообщение “САВ”. Для простоты будем использовать маленькие числа (на практике применяются гораздо большие).
59
1.Выберем p=3 и q=11.
2.Определим n=3*11=33.
3.Найдем (p-1)(q-1)=20. Следовательно, в качестве d, взаимно простое с 20, например, d=3.
4.Выберем число е. В качестве такого числа может быть взято любое число, для которого удовлетворяется соотношение
(е*3) (mod 20) = 1, например 7.
5.Представим шифруемое сообщение как последовательность целых чисел с помощью отображения: А→1, В→2, С→3. Тогда сообщение принимает вид (3,1,2).
6.Зашифруем сообщение с помощью ключа {7,33}.
ШТ1 = (37) (mod 33) = 2187 (mod 33) = 9, ШТ2 = (17) (mod 33) = 1 (mod 33) = 1, ШТ3 = (27) (mod 33) = 128 (mod 33) = 29.
Расшифруем полученное зашифрованное сообщение (9,1,29) на основе закрытого ключа {3,33}:
ИТ1 = (93) (mod 33) = 729 (mod 33) = 3, ИТ2= (13) (mod 33) = 1 (mod 33) = 1,
ИТ3 = (293) (mod 33) = 24389 (mod 33) = 2.
6.2 Однонаправленные хэш-функции
Центральным понятием в теории асимметричных криптографических криптографических систем является понятие односторонней функции.
У однонаправленной хэш-функции может быть множество имен: функция сжатия, функция сокращения contraction function, краткое изложение, характерный признак, криптографическая контрольнаясумма, кодцелостности сообщения. [2]
Хэш-функции, долгое время использующиеся в компьютерных науках, представляют собой функции, математические или иные, которые получают на вход строку переменной длины (называемую прообразом) и преобразуют ее в строку фиксированной, обычно меньшей, длины (называемую значением хэш — функции). В качестве простой хэш-функции можно рассматривать функцию, которая получает прообраз и возвращает байт, представляющий собойXOR всехвходныхбайтов.
Смысл хэш-функции состоит в получении характерного признака прообраза - значения, по которому анализируются
60
