Методы оптимизации ПИ 202з Тихонов РГР v2

В результате получился вот такой план:

	B1 0	B2 0	B3 0	B4 0	B5 0
A1 0	X11 40 7	X12 0 9	X13 0 10	X14 30 6	X15 50 5
A2 0	X21 0 12	X22 0 8	X23 20 6	X24 40 5	X25 0 13
A3 0	X31 0 6	X32 60 2	X33 0 8	X34 10 2	X35 0 4

Посчитаем кол-во ед. затрат:

Итого у меня получилось три плана:

1. План северо-западного угла с 1380 ед. затрат

2. План минимального элемента с 1230 ед. затрат

3. План аппроксимации Фогеля с 1170 ед. затрат.

Самый эффективный метод – это план аппроксимации Фогеля:

	B1	B2	B3	B4	B5
A1	X11 40 7	X12 0 9	X13 0 10	X14 30 6	X15 50 5
A2	X21 0 12	X22 0 8	X23 20 6	X24 40 5	X25 0 13
A3	X31 0 6	X32 60 2	X33 0 8	X34 10 2	X35 0 4

Задача №4. Решить задачу линейного программирования двумя (графическим и

симплекс-методом) методами.

Для изготовления двух видов продукции используется три вида сырья . При производстве единицы продукции первого вида затрачивается А1 кг сырья первого вида , А2 кг сырья второго вида и А3 кг сырья третьего вида . При производстве единицы продукции второго вида затрачивается Б1 кг сырья первого вида , Б2 кг сырья второго вида и Б3 кг сырья третьего вида . Запасы сырья первого вида составляют Запасы 1 кг , второго – Запасы 2 кг , третьего – Запасы 3 кг . Прибыль от реализации единицы продукции первого вида составляет С1 ден . ед ., прибыль от реализации единицы продукции второго вида составляет С2 ден . ед . Определить оптимальный план выпуска продукции , чтобы прибыль от реализации была максимальной .

Вариант	A1	A2	A3	Б1	Б2	Б3	Запасы1	Запасы2	Запасы3	С1	С2
19	15	22,5	25	7,5	30	20	575	525	625	45	50

Вид сырья	Продукция A	Продукция B	Запас сырья
1	15	7,5	575
2	22,5	30	525
3	25	20	625
Стоимость реализации	45	60

Решение.

Пусть х₁ и х₂ - это количество единиц продукции соответственно А и В, запланированных к производству. Для их изготовления потребуется

(15х₁ +7,5 х₂) единиц ресурса 1,

(22,5х₁ +30х₂) единиц ресурса II,

(25х₁ +20х₂) единиц ресурса III.

Так как, потребление ресурсов I, II, III не должно превышать их запасов, то связь между потреблением ресурсов и их запасами выразится системой неравенств:

 15х₁ +7,5х₂ ≤ 575;              

 22,5х₁ +30х₂ ≤ 525;          

25х₁ +20х₂ ≤ 625.               

По смыслу задачи переменные х₁ ≥ 0, х₂ ≥0.

Конечную цель решаемой задачи – получение максимальной прибыли при реализации продукции – выразим как функцию двух переменных х₁ и х₂.

Суммарная прибыль А составит 45х₁ от реализации продукции А и 50х ₂ от реализации продукции В, то есть : F = 45х₁ +50х _2. 

Изобразим многоугольник решений данной задачи.

В ограничениях задачи поменяем знаки неравенства на знаки равенства.

Проведем оси: на горизонтальной будут указываться значения переменной х₁, а на вертикальной — х₂ .Далее рассмотрим условие неотрицательности переменных: x₁ ≥ 0 и х₂ ≥ 0. Эти два ограничения показывают, что пространство допустимых решений будет лежать в первом квадранте (т.е выше оси x₁ и правее оси х₂).

Чтобы учесть оставшиеся ограничения, проще всего заменить неравенства на равенства, в результате чего получится система уравнений прямых:

 15х₁ +7,5х₂ = 575;     y1         

 22,5х₁ +30х₂ = 525;     y2     

25х₁ +20х₂ = 625.            y3   

а затем на плоскости провести эти прямые.

Теперь добавим вектор f = 45х₁ +50х₂max

По графику видно, что вектор f пересекается с функцией y1 в самом верхнем правом углу, значит для максимума необходимо найти x1 и x2 при пересечении вектора и этой функции.

15х₁ +7,5х₂ = 575

45х₁ +50х ₂=0

максимальное значение линейной функции равно :

F_max = 30*16,09 + 40*19,64 = 1232,80.

Итак, F_max = 1232,80 при оптимальном решении х₁ = 16,09, х₂ = 19,64, т. е. максимальная прибыль в 1232,80 ден. ед. может быть достигнута при производстве 16,09 единиц продукции А и 19,64 единиц продукции В.

Ответ: F_max = 1232,80 при х₁ = 16,09, х₂ = 19,64 .

Задача №5.

Пусть функция полезности имеет вид U=a₀x₁^a1x₂^a2

Даны коэффициенты:

а₀=1,25,

а₁=0,61,

а₂=0,46,

бюджет: B=320

цены: P₁=21,

P₂=26.

Составить математическую модель и найти оптимальный набор благ и его полезность с помощью метода множителей Лагранжа .

Построим функцию Лагранжа:

L= a₀x₁^a1x₂^a2+(B-P₁x₁-P₂x₂)

Возьмем частные производные по всем переменным и приравняем их нулю:

Преобразуем систему:

Разделим первое уравнение на второе:

Решим полученную систему:

Подставив численные значения x₁ и x₂, получим оптимальный набор благ:

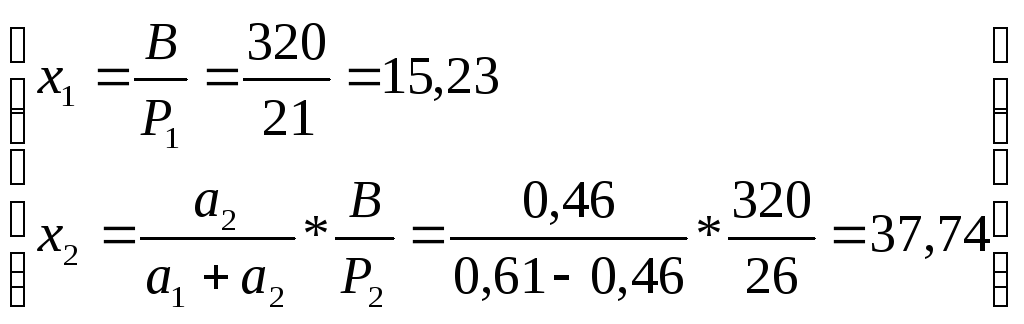
Вычислим полезность оптимального набора:

U=a₀x₁^a1x₂^a2=1,25*15,23^0,61*37,74^0,46=34,97

Ответ: x₁=15,23; x₂=37,74; U=34,97

33 из 33