
Методичка для тех.спец. математика
.PDF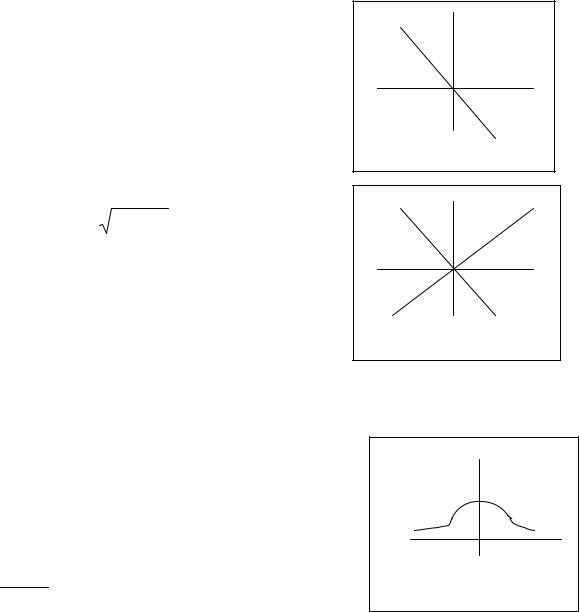
|
|
|
|
|
|
59 |
|
|
|
|
В прямоугольной декартовой системе координат указанные окрестности |
||||||||||
определяется соответственно условиями: (x − a )2 + (y − b)2 < δ2 , |
где M(a, b) |
|||||||||
(x − a)2 + (y − b)2 + (z − c)2 |
< δ2 , где M(a, b, c). |
|
|
|
||||||
ОПРЕДЕЛЕНИЕ 2. |
|
Точка |
M T называется внутренней точкой |
|||||||
множества T, если δ − окрестность т. M , принадлежащая T. |
|
|||||||||
ОПРЕДЕЛЕНИЕ 3. |
Множество T на плоскости (в пространстве) назы- |
|||||||||
вается открытым, если т. M T ее δ − окрестность, входящая в множе- |
||||||||||
ство T, то есть все точки T должны быть внутренними. |
|
|
|
|||||||
Множество T называется связным, если две точки этого множества |
||||||||||
можно соединить непрерывной линией, состоящей из точек множества T. |
||||||||||
Связное открытое множество называется областью. |
|
|
|
|||||||
2. ПРИМЕР 1. Найти область определения |
|
y |
|
|||||||
функции z = ln(− x − y) и изобразить ее. |
|
|
|
|||||||
Решение. |
− x − y > 0 , |
x + y < 0 . Рассмат- |
− x |
|
x |
|||||
риваем прямую x + y = 0 , y = −x y < −x . |
|
0 |
||||||||
Ответ: Множество точек плоскости, |
нахо- |
x |
|
x + y = 0 |
||||||
дящихся ниже прямой y = −x (прямая, содержа- |
|
|
|
|||||||
щая биссектрисы 2-го и 4-го координатных уг- |
|
Рис. 1 |
||||||||
лов). |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
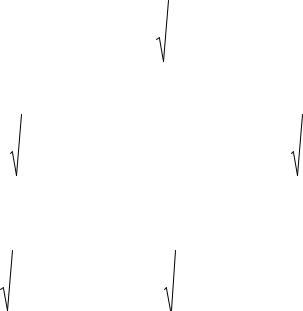
ПРИМЕР |
2. |
Найти |
область |
определения |
|
y |
|
|||
функции f(r,ϕ) = r |
cos 2ϕ и изобразить ее. |
|
|
|||||||
|
|
|
||||||||
Решение. |
cos2ϕ ≥ 0. Период функции ра- |
|
|
0 |
||||||
|
− π ≤ 2(ϕ + kπ) ≤ π , |
|
|
|
|
|
|
|||
вен π . |
|
|
|
|
|
|
x |
|||
|
2 |
|
2 |
|
|
|
|
|
|
|
− π − kπ ≤ ϕ ≤ π − kπ . |
В |
силу |
этого |
|
Рис. 2 |
|||||
|
4 |
|
4 |
|
|
|
|
|
||
− π ≤ ϕ + kπ ≤ π , k Z . |
|
|
|
|
|
|
|
|||
4 |
4 |
|
|
|
|
|
|
|
|
|
Ответ: Множество точек, ограниченное прямыми y = x и y = −x и со- |
||||||||||
держащее ось ox . |
|
|
|
|
|
|
|
y |
||
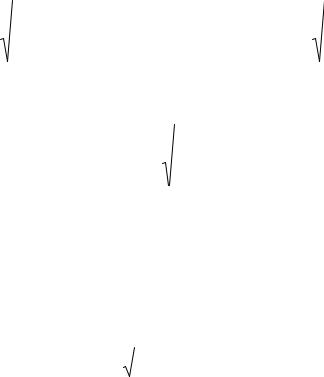
ПРИМЕР 3. Найти область определения |
|
|
||||||||
|
|
|
||||||||
функции z = arcsin[2y + (1 + x 2 )−1] и изобразить ее. |
|
|
|
|||||||
Решение. |
|
|
|
|
|
|
|
|
0 |
|
−1 ≤ 2y(1 + x 2 )−1 < 1, 0 ≤ 2y(1 + x 2 )≤ 2 , |
|
|
|
|||||||
|
|
|
x |
|||||||
0 ≤ y ≤ |
1 |
|
|
|
|
|
|
|
|
|
1 + x 2 . |
|
|
|
|
|
|
|
Рис. 3 |
||
Ответ: Множество точек, ограниченное ли- |
|
|
|
|||||||
ниями y = 0 |
и y = |
1 |
. (Рис. 3). |
1 + x2 |
60
§2. Частные производные и дифференциалы функций многих переменных. Касательная плоскость и нормаль поверхности
1. ОПРЕДЕЛЕНИЕ 1. Если для функции |
|
||
z = f (x, y) |
|
|
(1) |
точки M(x, y) и M* (x + |
x, y + |
y) D(z) − область определения функции |
|
(1), то |
|
|
|
z(x, y) = f (x + |
x, y + |
y) − f (x, y) |
(2) |
- полное приращение функции (1) в т. M(x, y) , которое соответствует прира-
щению |
x, |
|
y независимых переменных x, y ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
x z(x, y) = f (x + |
x, y) − f (x, y); |
y z(x, y) = f (x, y + |
y) − f (x, y) |
(3) |
|
||||||||||||||||||||||||||||||||
- частные приращения соответственно по независимым переменным x и y ; |
|
|||||||||||||||||||||||||||||||||||||
|
|
z′′(x, y) = lim |
|
x z = lim |
f (x + x, y) − f (x, y) |
|
|
|
|
|
(4) |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
x |
|
|
|
|
x→0 |
|
x |
|
x→0 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
- частная производная функции (1) по x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
z′′ |
(x, y) = lim |
|
y z(x, y) |
|
= lim |
f (x, y + |
x) − f (x, y) |
|
|
(5) |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
y |
|
|
|
|
x→0 |
|
|
y |
|
|
|
|
y→0 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
- частная производная функции (1) по y . Вместо z′x (x, y) |
употребляются обо- |
|||||||||||||||||||||||||||||||||||||
|
|
|
f |
x |
|
|
∂z(x, y), ∂f (x, y) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z′y |
: |
||||||||||||
значения |
′ (x, y), |
|
То |
же |
|
|
|
|
самое |
вместо |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f ′ (x, y), |
∂z(x, y), ∂f (x, y) . Из (4), (5) следует, чтобы найти частную производ- |
|||||||||||||||||||||||||||||||||||||
y |
∂y |
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ную z′x (zy′), |
надо дифференцировать функцию f (x, y) по x , считая y(x) по- |
|||||||||||||||||||||||||||||||||||||
стоянной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
x + y 2 |
|
|
|
|
|
x + y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Например, для z = |
|
1 − |
|
|
|
|
|
+ arcsin |
|
|
, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
x − y |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
x + y 2 ′ |
|
|
|
|
|
1 |
|
|
|
|
x + y |
′ |
|
|
|
|||||||||||||
z′ = |
|
|
|
|
|
|
|
|
1 |
− |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x + y |
2 |
|
|
xy |
|
|
|
|
|
x + y |
2 |
|
xy |
x |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x + y x + y ′ |
|
|
|
|
|
|
||||||||
|
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
xy |
|
|
|
|
|
1 |
|
|||||
= |
xy |
|
|
x |
+ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x + y 2 |
|
|
x + y 2 |
||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
1 − |
|
|
|
|
|
|
|
|
1 − |
|
|
||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
xy |
||||
x + y ′ |
|
||
|
|
|
= |
|
|||
|
|
|
|
|
xy x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
61 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
x + y x + y |
′ |
|
|
|
1 |
|
|
|
|
x + y |
|
|||||||||||||
= |
|
|
|
|
|
|
|
|
1 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
1 |
− |
|
|
× |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
x + y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + y 2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
xy xy |
|
|
x |
|
|
|
|
|
xy |
|
||||||||||||||||||
|
|
1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + y |
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|||||
|
xy − (x + y)y |
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
× |
= − |
|
|
|
|
xy |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
( xy) |
|
|
|
|
|
|
2 |
|
|
|
|
x + y 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
1 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. ОПРЕДЕЛЕНИЕ 2. Функция (1) называется дифференцируемой в т. M0 (x 0 , y0 ), если ее полное приращение (в т. M 0 ) представимо в виде
z(x0 , y 0 ) = f (x0 + x0 , y 0 + y 0 ) − f (x0 , y 0 ) = |
(6) |
||||||
= A(x0 , y 0 ) x0 + B(x0 , y 0 ) y 0 + |
0( ρ), |
||||||
|
|||||||
где |
|
|
|
||||
ρ = |
|
; lim |
0( |
ρ) |
= 0 , |
|
|
( x0 )2 + ( y 0 )2 |
(7) |
||||||
|
|
||||||
|
|
p→0 |
ρ |
|
|||
то есть в виде двух слагаемых: |
|
|
|
||||
I = A(x0 , y 0 ) x + B(x0 , y 0 ) y 0 ; |
II = 0( ρ), |
(8) |
|||||
где первое слагаемое I линейно относительно приращений x 0 , |
y0 независи- |
||||||
мых временных x и y в т. M 0 , а второе слагаемое II - БМ величина более высокого порядка малости, чем Δρ.
ОПРЕДЕЛЕНИЕ 3. Если функция (1) дифференцируема в т. M0 (x 0 , y0 ), то I слагаемое - главная часть полного приращения и функции -
называется дифференциалом (полным дифференциалом) функции |
(1) в |
т. |
M0 (x 0 , y0 ) и обозначается одним из символов dz(x 0 , y0 ), df (x 0 , y0 ). |
|
|
Итак, по определению, |
|
|
dz(x0 , y 0 ) = A(x0 , y 0 ) x0 + B(x0 , y 0 ) y 0 . |
(9) |
|
Справедливы равенства |
|
|
A(x0 , y 0 ) = fx′ (x0 , y 0 ) = fx′ (M 0 ); |
(10) |
|
B(x0 , y 0 ) = fy′′(x0 , y 0 ) = fy′′(M 0 ). |
|
|
|
|
|
Из (9), (10) следует |
|
|
dz(x0 , y 0 ) = df (x0 , y 0 ) = fx′ (x0 , y 0 ) x0 + fy′ (x0 , y 0 ) y 0 = |
|
|
= fx′ (M 0 ) x0 + fy′ (M 0 ) y 0 |
(11) |
|
При достаточно малом Δρ слагаемым II в (6) можно пренебречь. Это да- |
||
ет формулу приближенного вычисления значения функции z = f (x, y) |
в |
|
т. M(x 0 + x 0 , y0 + y0 ): |
|
|
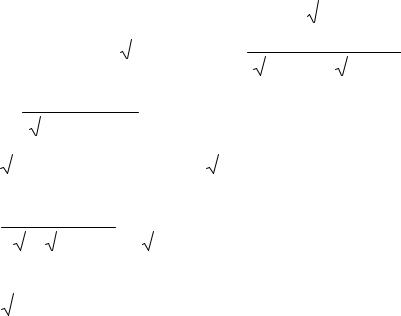
62
f (x0 + |
|
x0 , y 0 + y 0 ) ≈ f (x0 , y 0 )+ fx′ (x0 , y 0 ) |
x0 + fy′ (x0 , y 0 ) y 0 |
(12) |
||||||||||||||||||||||||||||||||||||||||||||||
ПРИМЕР 1. Вычислить приближенно lg( |
|
|
|
|
|
+ 2,033 ). |
|
|||||||||||||||||||||||||||||||||||||||||||
|
3,99 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = lg( |
x + y3 ), |
z′x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Решение. |
|
= |
( |
|
+ y3 )2 |
|
|
|
ln10 |
; |
|
|
||||||||||||||||||||||||||||||||||||||
x |
x |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
z′y = |
|
|
|
|
|
|
|
3y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
( |
|
|
|
|
+ y3 )ln10 |
; x 0 |
= 4; y0 |
= 2; x 0 |
|
= −0,01; |
y = 0,03 . |
|
||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
lg[ |
|
|
|
|
|
|
|
|
+ (y + y)3 ]≈ lg( |
|
+ y3 )+ |
1 |
× |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
x + x |
x |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln10 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
3y2 |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
× |
2 |
|
|
|
( |
|
|
|
|
+ y3 )+ |
|
( |
|
|
|
|
|
+ y |
3 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x |
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для нашего случая имеем |
|
|
|
|
− 0,01 |
|
|
|
12 0,03 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
lg( |
|
3,99 + 2,033 )≈ lg10 + |
|
|
|
+ |
= |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
40 |
|
|
|
10 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= 1 + |
|
|
1 |
|
|
|
|
(− 0,01 +1,44) = 1 + |
1,43 |
|
|
≈ 1,0155 . |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
40 ln10 |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
40 ln10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Ответ: 1,0155 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ПРИМЕР 2. Найти дифференциал функции u = x yz . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Решение. |
Находим частные производные |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
(ln u)′ |
= |
|
|
(yz ln x)′ |
|
|
= |
|
yz |
; u′ |
= x yz −1 y z ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(ln u)′y |
|
= |
u′y |
= (yz ln x)′y = (ln x)(yz )′y = zyz−1 ln x . |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
u′ |
= x yz zy z−1 ln x = y z x yz |
ln x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
y |
|
|
|
|
|
= (yz ln x)′z ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
(ln u)′z |
|
u′z |
= (ln x)yz ln y ; u′z = x yz (ln x)y z ln y . |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Согласно (3) имеем |
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
du(x, y, z) = x y−1 y z dx + yz x yz |
ln xdy + x yz (ln x)y z ln ydz . |
|
||||||||||||||||||||||||||||||||||||||||||||||||
Ответ: |
x y−1 y z dx + y z x yz |
ln xdy + x yz (ln x)y z ln ydz . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
3. ОПРЕДЕЛЕНИЕ 4. |
|
|
Касательной плоскостью |
α поверхности ω: |
||||||||||||||||||||||||||||||||||||||||||||||
F(x, y, z) = 0 в т. M0 ω называется плоскость, в которой |
содержатся все ка- |
|||||||||||||||||||||||||||||||||||||||||||||||||
сательные к линиям ω и проходящим через т. M 0 . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
ОПРЕДЕЛЕНИЕ 5. |
|
|
|
|
Нормалью к ω в т. |
M0 ω , |
называется прямая, |
|||||||||||||||||||||||||||||||||||||||||||
проходящая через т. M0 |
|
касательной плоскости α . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
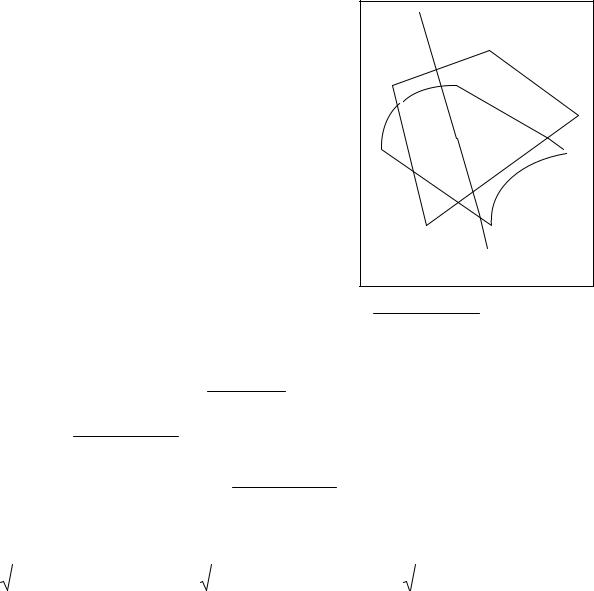
63 |
|
Если поверхность ωзадана общим уравнением |
|
ω : F(x, y, z) = 0 |
(13) |
иM0 (x 0 , y0 , z0 ) ω : F(x 0 , y0 , z0 ) = 0 , то уравнение касательной плоскости
αимеет вид
α : Fx′ (M0 )(x − x0 ) + Fy′ (M0 )(y − y0 ) + Fz′(M0 )(z − z0 ) = 0 , |
(14) |
где x, y, z − |
координаты |
текущей |
точки |
T(x, y, z) касательной плоскости; |
|
||
x 0 , y 0 , z 0 − |
координаты |
точки |
касания |
M 0 (x 0 , y0 , z0 ) (см. рис. 3). |
|
|
|
Уравнение нормали к ω в т. M0 (x 0 , y0 , z0 ) есть
|
x − x |
0 |
|
y − y |
0 |
|
z − z |
|
|
l : |
|
= |
|
= |
0 |
, |
(15) |
||
F′′(M |
) |
F′′(M |
) |
F′′(M ) |
|||||
|
x |
0 |
|
y |
0 |
|
z 0 |
|
|
где P(x, y, z) − текущая точка нормали l (см.
рис. 4).
ПРИМЕР 3. Найти уравнение касательной
l
P •
•T
•M 0
Рис. 4
плоскости и нормали к поверхности ω : 4 + 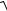
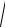 x 2 + y 2 + z 2 = x + y + z в
x 2 + y 2 + z 2 = x + y + z в
т. M0 (2,3,6).
Решение. M 0 ω : 4 + 
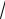 4 + 9 + 36 = 2 + 3 + 6; 11 = 11.
4 + 9 + 36 = 2 + 3 + 6; 11 = 11.
ω : 4 + 
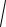 x 2 + y 2 + z 2 − x − y − z = 0
x 2 + y 2 + z 2 − x − y − z = 0
(см. 13) F(x, y, z) = 4 + 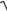
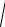 x 2 + y2 + z 2 − x − y − z ;
x 2 + y2 + z 2 − x − y − z ;
F′ |
= |
|
|
|
|
|
x |
−1; F′ = |
|
|
|
|
y |
|
−1; F′ |
= |
|
|
|
|
|
z |
|
−1. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x |
|
|
|
|
x 2 + y2 + z 2 |
y |
|
|
|
x |
2 + y2 + z 2 |
|
|
|
|
z |
|
|
|
x 2 + y2 + z 2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
F′ |
(M |
|
) = |
2 |
−1 = − |
5 |
; F′ (M |
|
) = |
3 |
−1 = − |
4 |
; F′(M |
|
) = − |
1 |
. |
|
|
|
|||||||||||||||
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
||||||||||||||||||||||||
x |
|
|
7 |
7 |
y |
|
|
|
7 |
7 |
|
|
z |
|
|
|
7 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Согласно (14) и (15) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
α : 5(x − 2) + 4(y − 3) + (z − 6) = 0; l : |
x − 2 |
= |
y − 3 |
= |
z − 6 |
. |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
4 |
|
|
1 |
|
|
|
||||
64
Ответ: |
|
5(x − 2) + 4(y − 3) + (z − 6) = 0; |
x − 2 |
= |
y − 3 |
|
= z − 6 . |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
4 |
|
|
|
|
|
|
||||
§3. Производная функции, заданной неявно. Экстремум функций |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
двух переменных |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1. Если функция z от двух независимых переменных x и y задана неяв- |
||||||||||||||||||||||||||||||||||||||||||||
но: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω : F(x, y, z) = 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
||||||||||||||||
то ее первые частные производные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
′′(x, y) = − |
F′′(x, y, z) |
|
|
z′′(x, y) = − |
Fy′ (x, y, z) |
|
|
|
|||||||||||||||||||||||||||||||||||
z |
|
x |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
. |
|
(2) |
||||||||||||||||||||||||
Fz′′(x, y, z) |
Fz′′(x, y, z) |
|
||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
К формулам (2) можно придти, дифференцируя почленно (1) частным об- |
||||||||||||||||||||||||||||||||||||||||||||
разом по x и по y и учитывая зависимость z = z(x, y). |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
ПРИМЕР 1. |
z = x + arctg |
|
y |
|
, z′x |
= ?, |
|
z′y |
= ?. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
z |
− x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
I способ. z − x − arctg |
|
y |
|
|
= 0 . Согласно (1) и (2) |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
z − x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
y |
|
′ |
|||||||||||||||
F = z − x − arctg |
|
|
|
|
|
|
|
|
; |
F′ |
= −1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
z − x |
|
x |
|
|
|
|
|
|
|
|
|
y |
|
2 |
|
|
z − x x |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 + |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
− x |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|||||
= − 1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − 1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
(z |
− x)2 + y2 |
|
|
|
|||||||||||||||||||||||
|
|
|
y |
|
|
|
|
(z − x)2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
z − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
y |
′ |
|
|
|
|
|
z − x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
F′ = − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
)2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
y |
|
|
|
y |
|
2 |
|
|
|
z − x |
|
y |
|
|
|
|
|
|
|
+ y |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z − x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
z − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
′ |
|
|
|
|
|
(z − x)2 |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|||||||||||||||
Fz′ = |
1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z − x)2 + y2 |
|
|
(z − x)2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
1 + |
|
|
|
2 |
z − x |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
z |
− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= 1 + |
|
|
|
|
|
y |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
(z − x)2 + y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
z′ = 1; z′ |
= |
|
|
|
|
|
z − x |
|
|
|
|
|
|
|
(z − x)2 + y2 |
|
|
|
= |
|
|
|
|
|
|
|
z − x |
|
. |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x |
|
|
|
|
y |
|
|
|
(z |
− x)2 + y2 (z − x)2 + y2 + y (z |
|
|
− x)2 + y2 + y |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
Ответ: −1; |
|
|
|
|
|
z − x |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
(z − x)2 + y2+y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
y ′ |
|
|
|
||||||
II способ. Согласно замечанию z′x |
= 1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + |
|
|
|
|
y |
|
|
|
|
z − x |
x |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
(z′x −1) |
|
|
|
|
|
|
|
y(z′x |
|
−1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
||||||||||||||||||
= 1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 + |
|
|
|
|
|
|
|
|
|
|
|
|
; z |
′x 1 |
− |
|
|
|
|
|
|
|
|
= |
|||||||||||||||
|
|
|
|
y |
|
|
|
|
|
(z |
− x)2 |
|
|
|
|
|
|
|
|
|
|
|
(z |
− x)2 |
+ y2 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
(z − x)2 + y2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
z − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= 1 − |
|
|
|
|
|
y |
|
|
|
|
|
|
|
; z′x = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
(z − x)2 + y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Аналогично, z′ |
= |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
y ′ |
= |
(z − x) − y(z′y ) |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
)2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
2 z |
− x |
y |
|
− x |
+ y |
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 + |
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z − x |
|
|
|
|
|
|
|
|
|
|||||||||||
z′y 1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
; z′y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||||
(z − x)2 |
|
+ y2 |
|
|
(z − x)2 + y2 |
|
(z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− x)2 + y2 + y |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Получаем тот же результат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
2. Напомним, |
что δ − окрестностью т. M0 (x 0 , y0 ) называется открытый |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
круг с центром в т. M 0 |
и радиуса δ : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
(x − x0 )2 + (y − y 0 )2 < δ2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
||||||||||||||||||||||||||||||
|
66 |
|
|
|
ОПРЕДЕЛЕНИЕ 1. Говорят, что функция |
|
|
|
|
z = f (x, y) достигает локального максимума (ло- |
y |
|
|
|
кального минимума) в |
т. M0 (x 0 , y0 ), если |
|
M |
• δ |
δ − окрестность т. M 0 , |
что для всех ее точек |
|
||
|
|
|||
M(x, y) имеет место |
|
|
|
|
f (x 0 , y0 ) ≥ f (x, y) |
(f (x 0 , y0 ) ≤ f (x, y)) |
0 |
|
x |
|
Рис. 1 |
|||
|
|
|
|
|
Локальный минимум и локальный максимум функции принято называть локальными экстремумами.
Теорема 1. (Необходимое условие локального экстремума). Если функция z = f (x, y) достигает локального экстремума в т. M0 (x 0 , y0 ) и в этой точке
частные производные, то
|
∂f |
(M |
0 ) = 0 |
|
∂x |
||
|
|
|
|
|
∂f (M 0 ) = 0 |
||
|
|
|
(4) |
∂y
В случае (4) т. M 0 (x 0 , y0 ) называется стационарной точкой функции z = f (x, y).
Теорема 2. (Достаточное условие локального экстремума). При выполнении условия (4)
A = f ′′ |
(M |
0 |
), B = f ′′ |
(M |
0 |
), C = f ′′ |
(M |
0 |
). |
xx |
|
xy |
|
yy |
|
|
=A B , B C
(5)
(6)
если > 0 , то функция z = f (x, y) имеет в точке M 0 локальный экстремум, а именно: локальный максимум при A < 0 (или C < 0 ) и локальный минимум при A > 0 (или C > 0 ); если < 0 , то в т. M 0 локального экстремума нет; если же = 0, то вопрос остается открытым.
ПРИМЕР 2. Найти экстремум функции z = −x 2 + 3x − xy − y2 + 6y .
Решение. z′x = −2x + 3 − y; z′y = −x − 2y + 6

67
|
|
|
xx |
|
= − |
xy = − |
1; |
yy |
= − |
2. |
|
|
|
|
|
|
|
|
(4): |
|
||||
|
|
|
z′′ |
2; |
z′′ |
z′′ |
|
|
|
|
Составляем |
систему |
2x + y = 3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 2y = 6 |
= |
|
2 |
1 |
|
= 3; |
x = |
|
3 |
1 |
|
= 0; |
y |
= |
|
2 |
3 |
|
= 9; |
x 0 = 0; y0 |
= 3; |
M0 (0,3). |
|||
|
|
|
|
|
|
|||||||||||||||||||
|
|
1 |
2 |
|
|
|
|
6 |
2 |
|
|
|
|
|
|
1 |
6 |
|
|
|
|
|
|
|
A − 2 < 0; B = −1; C = −2 < 0; |
= |
|
− 2 |
−1 |
|
= 3 > 0 . |
|
|
||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
−1 |
|
|
|
|
|
||||
Ответ: M0 (0,3) − точка локального максимума.
3. Чтобы найти наибольшее и наименьшее значения непрерывной функции в ограниченной замкнутой области D , надо:
1)найти стационарные точки D и значения функции в этих точках;
2)найти наибольшее и наименьшее значения функции на границе ∂D области D ;
3)из всех найденных значений выбрать наибольшее и наименьшее.
|
ПРИМЕР |
3. |
|
Найти |
наименьшее и наибольшее |
значения |
функции |
||||||||
z = cos x cos y cos(x + y) в замкнутой области 0 ≤ x ≤ π, |
0 ≤ y ≤ π. |
|
|
||||||||||||
|
Решение. |
|
|
|
z′x |
= − sin x cos y cos(x + y) − cos x cos y sin(x + y), |
|||||||||
z′y |
= − cos x sin y cos(x + y) − cos x cos y sin(x + y); |
|
|
|
|
|
|||||||||
cos y sin(2x + y) = 0 |
|
|
|
|
|
|
|
|
|||||||
|
|
sin(x + 2y) = 0 |
|
|
|
|
|
|
|
|
|||||
cos x |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
y |
|
|
|
|
|
||
|
cos y = 0 |
|
x |
2 |
|
|
π |
C |
|
B |
|
|
|||
I) |
|
|
|
|
|
согласно условно задачи. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||
|
cos x = 0 |
|
|
= |
π |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
π |
π |
|
|
|
|
|
|
|
|
A |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
0 |
|
π |
x |
|
||||
|
z |
, |
= 0 ; |
|
|
|
|
|
|
|
|||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
Рис. 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
68 |
|
|
|
|
|
|
|
|
|
|
|
|
sin(2x + y) = 0 |
|
|
2x + y = 0, π |
M |
|
|
(0,0); |
M |
|
π |
π |
||||||||||||||||||||
II) |
|
+ 2y) = |
0 |
|
x |
+ 2y |
= 0, π |
|
|
|
; |
|
|||||||||||||||||||
sin(x |
|
|
|
|
|
|
1 |
|
|
|
|
2 |
3 |
3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
π |
|
π |
|
|
|
|
1 |
|
|
|
|
2π |
|
|
1 |
|
|
|
|
|
|
|
||||
z(0,0) = 1; z |
|
, |
|
|
= |
|
|
|
|
cos |
|
= − |
|
|
|
|
. |
|
|
|
|
|
|
||||||||
|
3 |
|
4 |
|
|
3 |
8 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
cos y = 0 |
|
|
|
|
|
|
|
|
|
= |
π |
|
|
|
|
|
|
= |
π |
|
|
π |
|||||||||
|
|
|
|
|
|
|
y |
2 |
|
|
|
y |
2 |
|
|||||||||||||||||
III) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
0, |
= 0 . |
|||||||||||
sin(x + 2y) = |
0 |
|
|
|
|
+ 2y |
= 0, π |
|
|
|
= 0 |
|
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
||||||||||||||
sin(2x + y) |
|
|
y = 0 |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
π |
|
|
|
= 0 |
|
|
|
|
|
||||||||||||||||
IV) |
|
|
|
|
|
|
|
= |
|
|
|
|
z |
,0 |
|
|
|
|
|
||||||||||||
cos x = 0 |
|
|
|
x |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y = 0 |
|
|
|
|
|
z = cos |
2 |
x; |
|
z(0,0) = 1; |
|
|
|
π |
|
= 0 , так как |
|||||||||||||||
OA : |
≤ x |
≤ π |
|
|
|
|
|
|
z = |
,0 |
|||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
z′x = −2 sin x cos x = 0; |
|
x = |
|
π |
, π; |
|
|
|
|
|
|
|
|
π |
|
= z(π,0) = 0 |
|||||||||||||||
|
0, |
z(0,0) = z |
,0 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
x = π |
|
|
|
|
z = − cos y cos(π + y) = cos2 y; |
z(π,0) = 1; |
|||||||||||||||||||||||||
AB : |
≤ y |
≤ π, |
|
|
|||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z(π, π) = 1; y = |
π |
|
|
|
π |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
; z π, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y = π |
|
|
|
z = cos2 x . Этот случай уже рассматривался. |
|||||||||||||||||||||||||||
BC : |
≤ x |
≤ π, |
|||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x = 0 |
|
|
|
z = cos 2 y . Этот случай уже рассматривался. Получили три |
|||||||||||||||||||||||||||
OC : |
≤ y |
≤ π, |
|||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
различных значения z : − |
1 |
,0,1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: − |
1 |
− наименьшее значение, |
|
которое достигается во внутренней |
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
π π |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
− наибольшее значение, которое достигается в граничных точ- |
|||||||||||||||||||||||||||||
точке |
, |
; 1 |
|||||||||||||||||||||||||||||
3 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ках (0,0), (π, π), (0, π), (π,0).
