
Теоретические задачи
.pdf1.Доказать, что если линейный оператор  – невырожден, то
– невырожден, то  и
и  -¹ имеют одни и те же собственные векторы. Найти связь между собственными значениями этих операторов.
-¹ имеют одни и те же собственные векторы. Найти связь между собственными значениями этих операторов.
2.Доказать, что если x – собственный вектор оператора  , относящийся к собственному значению
, относящийся к собственному значению  , то x будет собственным вектором и для оператора
, то x будет собственным вектором и для оператора  где
где  – произвольный многочлен степени n. Найти соответствующее собственное значение оператора
– произвольный многочлен степени n. Найти соответствующее собственное значение оператора  .
.
3.Найти характеристический многочлен оператора  , действующего в трехмерном евклидовом пространстве
, действующего в трехмерном евклидовом пространстве  по формуле
по формуле 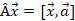 , где
, где  – фиксированный вектор.
– фиксированный вектор.
4.Найти собственные значения и собственные векторы оператора  , действующего
, действующего
втрехмерном евклидовом пространстве  по формуле
по формуле  , где
, где  – фиксированный вектор.
– фиксированный вектор.
5.Привести пример линейных операторов  и
и  , таких, что
, таких, что  .
.
6.Доказать, что оператор 
1) положителен
положителен  когда для любого x
когда для любого x
 |Â*x|.
|Â*x|.
2) нормален
нормален  когда для любого
когда для любого  оператор
оператор 
 также нормален.
также нормален.
(
7.Доказать, что в положительно определенной квадратичной форме
 все коэффициенты при квадратах неизвестных
все коэффициенты при квадратах неизвестных
положительны и что это условие не является достаточным для положительной определенности формы.
8.Доказать, что ортогональное дополнение  к линейному подпространству
к линейному подпространству  евклидова (унитарного) пространства
евклидова (унитарного) пространства  является линейным подпространством пространства
является линейным подпространством пространства  . В случае, если
. В случае, если  ,
,  найти
найти  .
.
9.В пространстве  заданы две квадратичные формы
заданы две квадратичные формы  и
и  . Можно ли одним невырожденным преобразованием привести их к каноническому виду? Если можно, то указать это преобразование. Если нельзя, то доказать это утверждение.
. Можно ли одним невырожденным преобразованием привести их к каноническому виду? Если можно, то указать это преобразование. Если нельзя, то доказать это утверждение.
10.Доказать, что сумма и пересечение подпространств  и
и  , инвариантных относительно оператора
, инвариантных относительно оператора  , также инвариантны относительно оператора
, также инвариантны относительно оператора  .
.
11.Дать определения нормальных и унитарных операторов. Связь между ними. Будет ли нормальный оператор унитарным и наоборот. Если да, то доказать это утверждение. Если нет, то также доказать. Будет ли произведение унитарных (нормальных) операторов в свою очередь унитарным (нормальным) оператором? Если да, то доказать. Если нет, то также доказать или привести контрпример.

12.Доказать, что если  , где
, где  и
и  перестановочны,
перестановочны,  – эрмитово,
– эрмитово,  – унитарно, то
– унитарно, то  – нормальное преобразование.
– нормальное преобразование.
13.Доказать, что если  и
и 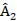 – самосопряженные преобразования, то самосопряженными будут и преобразования:
– самосопряженные преобразования, то самосопряженными будут и преобразования:
 и
и  .
.
14.Доказать, что произведение двух унитарных преобразований есть снова унитарное преобразование.
15.Показать, что если  – унитарное преобразование, а
– унитарное преобразование, а  – самосопряженное преобразование, то преобразование
– самосопряженное преобразование, то преобразование  – также самосопряженное.
– также самосопряженное.
16.Доказать, что если  – самосопряженное преобразование то преобразование
– самосопряженное преобразование то преобразование
существует и является унитарным. ( здесь – тождественное преобразование).
17. Пусть  – унитарное преобразование. Доказать, что если преобразование
– унитарное преобразование. Доказать, что если преобразование  обратимо, то преобразование
обратимо, то преобразование  – самосопряженное.
– самосопряженное.
(здесь – тождественное преобразование).
18.Доказать, что всякое инвариантное собственное подпространство линейного
преобразования 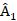 является также инвариантным подпространством линейного преобразования
является также инвариантным подпространством линейного преобразования  если преобразования
если преобразования  и
и  коммутируют.
коммутируют.
19.Доказать теорему Гамильтона-Кэли о том, что матрица линейного преобразования
 в
в  удовлетворяет его характеристическому уравнению, для частного случая n=2.
удовлетворяет его характеристическому уравнению, для частного случая n=2.
20.Доказать, что множество  линейных операторов над пространством
линейных операторов над пространством 
– линейное пространство и найти его размерность
21.Доказать, что для любых двух подпространств  и
и  конечномерного пространства
конечномерного пространства  таких, что
таких, что  существует линейный оператор
существует линейный оператор  , действующий в пространстве
, действующий в пространстве  , такой, что
, такой, что  и
и  .
.
22.Доказать, что ядро  и образ
и образ  любого линейного оператора
любого линейного оператора  ,
,
действующего в пространстве  , являются линейными подпространствами пространства
, являются линейными подпространствами пространства  , причем ядро и образ любого оператора
, причем ядро и образ любого оператора  являются инвариантными подпространствами относительно оператора
являются инвариантными подпространствами относительно оператора  .
.
23.Найти собственные значения и собственные векторы оператора сопряженного к
оператору  , действующего в трехмерном евклидовом пространстве
, действующего в трехмерном евклидовом пространстве  по формуле
по формуле  , где
, где  – фиксированный вектор.
– фиксированный вектор.
24.Пусть в трехмерном евклидовом пространстве  задан оператор
задан оператор  равенством
равенством
 где
где  – фиксированный вектор.
– фиксированный вектор.
1)Найти сопряженный к нему оператор  *,
*,
2)Показать, что  – нормальный оператор,
– нормальный оператор,
3)Является ли этот оператор ортогональным?
25.Доказать, что пересечение подпространств  и
и  и сумма подпространств
и сумма подпространств  и
и
 также являются подпространствами.
также являются подпространствами.
26.Доказать, что если  и
и  – положительно определенные преобразования, из которых одно не вырождено, то преобразование
– положительно определенные преобразования, из которых одно не вырождено, то преобразование  имеет неотрицательные собственные значения.
имеет неотрицательные собственные значения.
