
otvety_MO_1
.pdf
|
|
|
|
|
|
МЕТОДЫ ОПТИМИЗАЦИИ |
|
|
1. Математическая постановка задачи оптимизации. |
|
|||||||
Задача общего вида: f(x)→min/max, x A |
|
|
||||||
Если стоит задача минимизировать f(x) при ограничениях |
|
|||||||
|
|
|
|
|
|
hk(x)=0, k=1, ..., K, |
|
|
|
|
|
|
|
|
gj(x) |
0 j=1, ..., J, |
|
|
|
|
|
|
|
xi(u) xi xi(l), i=1, ..., N |
|
|
то это называется задачей оптимизации с ограничениями или задачей условной оптимизации. |
||||||||
Задача, в которой нет ограничений, т.е. |
|
|
||||||
|
|
|
|
|
|
|
J=K=0; |
|
|
|
|
|
|
|
xi(u)= - xi(l) = ∞, i=1, ..., N, |
|
|
называется |
|
оптимизационной |
задачей без |
ограничений или |
||||
задачей безусловной оптимизации. |
|
|
||||||
2. Простейшая классификация задач оптимизации. |
|
|||||||
1) |
Одномерные |
|
|
|||||
|
x {x } |
|
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
f (x) min/ max, x A |
|
|
|||||
|
A [a;b]; x [a;b] |
|
|
|||||
2) |
Многомерные |
|
|
|||||
|
n 2 |
|
|
|
|
|
|
|
|
x {x |
, x ,...x } |
|
|
||||
|
1 |
|
2 |
n |
|
|
|
|
|
f (x) f (x |
, x |
,...x ) min/ max, x A |
|
|
|||
|
|
|
|
1 |
2 |
n |
|
|
|
A R |
n |
безусловная многомерная оптимизаци |
|
|
|||
|
|
|
|
|
||||
|
A R |
n |
условная многомерная оптимизаци |
|
|
|||
|
|
|
|
|||||
3. Понятие о численных методах оптимизации. Методы поиска нулевого, первого и второго порядков. Пассивные и активные (последовательные) методы поиска.
Любой численный метод (алгоритм) решения задачи оптимизации основан на точном или приближенном вычислении ее характеристик (значений целевой функции, функций, задающих допустимое множество, а также их производных). На основании полученной информации строится приближение к решению задачи – искомой точке минимума х* или, если такая точка не единственна, – к множеству точек минимума. Иногда, если только это и требуется, строится приближение к минимальному значению целевой функции
Алгоритмы, использующие лишь информацию о значениях минимизируемой функции, называются алгоритмами нулевого порядка; алгоритмы, использующие также информацию о значениях первых производных, – алгоритмами первого порядка; алгоритмы, использующие, кроме того, информацию о вторых производных, – алгоритмами второго порядка.
Если все точки выбираются одновременно до начала вычислений, то алгоритм минимизации называется
пассивным.
Однако для решения большинства задач точки вычисления выбираются поочередно, т. е. точка
xi 1
выбирается, когда уже выбраны точки предыдущих вычислений x1...xi и в каждой из них
произведены предусмотренные алгоритмом вычисления, результаты которых будем обозначать
соответственно через
y |
...y |
1 |
i |
Такие алгоритмы называются последовательными.
4. Конечно шаговые и бесконечно шаговые методы поиска. Сходимость методов. Условия останова методов поиска.
Конечношаговыми (или конечными) называются методы, гарантирующие отыскание решения задачи за конечное число шагов.
Для бесконечно шаговых методов достижение решения гарантируется лишь в пределе.
Важной характеристикой бесконечношаговых методов является сходимость.
Метод сходится если xk x*,при k где x* , где - решение задачи
Условие остановки может определяться имеющимися в наличии вычислительными ресурсами (например, числом вычислений характеристик минимизируемой функции ) .
1

На практике часто используют следующие условия остановки:
x |
k t |
x |
k |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
f (x |
k t |
) |
f (x |
k |
) |
|
|
||||
|
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f (x |
k t |
) |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
5.Терема существования решения оптимизационной задачи.
x A, f (x) |
|
|
Если существует А, на которое задано f (x) |
||
1) A ограниченное |
|
|
2) А замкнутое |
|
|
|
||
|
|
|
3) f (x) на А непрерывна |
|
|
существует x* A : f (x*) min f (x);(x A) |
||
существует x ** A : f (x **) max f (x);(x A) |
||
6.Необходимые условия экстремума первого порядка (гладкие функции одной переменной).
f (x*) 0, где x * точка минимума (максимума)
7.Необходимые условия экстремума первого порядка (гладкие функции многих переменных).
|
t |
(x |
* |
, x |
* |
...x |
* |
) 0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
1 |
|
2 |
n |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
(x |
*, x *...x |
*) 0 |
|
|
|
|
|
|
|
|
|||||||
|
|
* |
|
* |
|
* |
|
* |
|
|||||||||
x |
|
1 |
|
2 |
n |
|
|
(x |
, x |
...x |
) |
|||||||
|
|
|
|
|
|
|
|
|
|
, где x |
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
n |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. . . . . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
*, x *...x |
|
*) 0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
x |
|
1 |
|
2 |
n |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.Одномерная безусловная оптимизация. Постановка задачи.
Задача одномерного поиска формулируется следующим образом: требуется найти максимум (минимум) функции одной переменной f(x), заданной на единичном отрезке.
x*=argmin (max) f(x), x принадлежит X. X–множество допустимых точек, среди которых ищется x*. X=[a, b] – отрезок неопределенности. А относительно f(x), предполагают, что она унимодальна.
9.Унимодальная функция. Лемма о свойстве унимодальных функций.
Функция f(x) называется унимодальной на отрезке [a,b], если она непрерывна на этом отрезке и существуют числа и , a≤ ≤ ≤b, такие что:
1)если a< , то на отрезке [a, ] функция f(x) монотонно убывает
2)если <b, то на отрезке [ ,b] функция f(x) монотонно возрастает
3)при x [ , ] выполняется f(x)=min f(x)
Свойства унимодальных функций:
1)Любая из точек локального минимума унимодальной функции является и точкой ее глобального минимум на отрезке [a,b].
2)Функция, унимодальная на отрезке [a,b], унимодальна и на любом меньшем отрезке [c,d] [a,b].
3)Пусть f(x) унимодальна на [a,b] и a≤x1<x2≤b. Тогда:
если f(x1)≤f(x2), то x* [a,x2], если f(x1)>f(x2), то x* [x1,b]
10.Пассивные методы поиска экстремума.
2

Пассивный поиск. x(1), x(2)… x(n) A, набор точек, в которых необходимо произвести вычисления, задается до начала самих вычислений. f(x||)… f(x(n)) с точностью , ||x*-||.
11.Метод перебора.
Метод перебора или равномерного поиска является простейшим методом минимизации и заключается в следующем. Разобьем отрезок [a, b] на N+1 равных частей точками деления
b a . Вычислим значения f(x) в точках . Найдем точку xl , для которой значение
xi a i( N 1),i 1, N
целевой функции минимально |
f (x ) min |
f (x |
) |
. Далее положим ̃= , ̃= ( ). Точность |
|
|
|
||||
|
l |
1 i N |
i |
|
|
|
|
|
|
|
|
найденного решения ̃определяется по формуле:
| x x* | |
|
|
b a |
|
гарант |
N 1 |
|||
|
|
|||
|
|
|
Если необходимо найти приближенное решение с заданной точностью ε, то минимальное число экспериментов N для достижения этой точности определяется из условия
|
|
|
b a |
|
|
|
||
гарант |
N |
1 |
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|||
N N |
|
|
min{N : N |
b a |
1} |
|||
расчет |
|
|||||||
|
|
|
N Z |
|
||||
|
|
|
|
|
|
|||
12. Алгоритм оптимального пассивного поиска. Теорема об оптимальности пассивного поиска.
Минимаксный метод поиска, в котором информация о значениях функции, вычисленных в предшествующих точках, не может быть использована, называют оптимальным пассивным поиском.
Алгоритм:
Отрезок [a,b] исходный отрезок неопределенности. Пусть N - число точек, в которых необходимо провести вычисления целевой функции f(x), т.е. N экспериментов. Точки, в которых необходимо провести эксперименты, определяются следующим образом:
Среди вычисленных значений {f(xi)} (i=1,N), ищется точка xj, в которой достигается минимум:
f(xj)= min f(xi) 1iN
Найденная точка принимается за приближенное решение задачи . Исходный отрезок неопределенности [a,b] после экспериментов в N точках сужается до [xj-1,xj+1], длина которого равна: LN.
Точность найденного решения равна половине отрезка неопределенности, т.е. , где и x* - точное решение.
Теорема
1) Если N=2k-1, то предлагаемый алгоритм является оптимальным.
2)Если N=2k то оптимального алгоритма не существует. Предлагаемый алгоритм является оптимальным.
2)
все четные точки раскидываются оптимально
Формула для вычисления четных точек: |
x |
|
2 j |
a j, j 1,2..k(k 1 / 2n)
13.Поразрядный поиск.
Вэтом методе перебор точек отрезка происходит сначала с шагом ∆= +1 − > до тех пор, пока не выполнится условие ( ) ≤ ( +1 ) или пока очередная из этих точек не совпадет с одним из концов отрезка. После этого шаг уменьшается (обычно в 4 раза) и перебор точек с новым шагом производится в противоположном направлении до тех пор, пока значение f(x) снова не перестанет уменьшаться или очередная точка не совпадет с другим концом отрезка и т.д. Описанный процесс завершается, когда перебор в данном направлении закончен, а использованный при поиске шаг не превосходит точности ε. Таким образом, шаг перехода в следующую точку может быть положительным или отрицательным в зависимости от направления движения.
14.Метод дихотомии.
Вэтом методе пробные точки x1 и x2 располагаются близко к середине очередного отрезка.
Схема алгоритма.
3
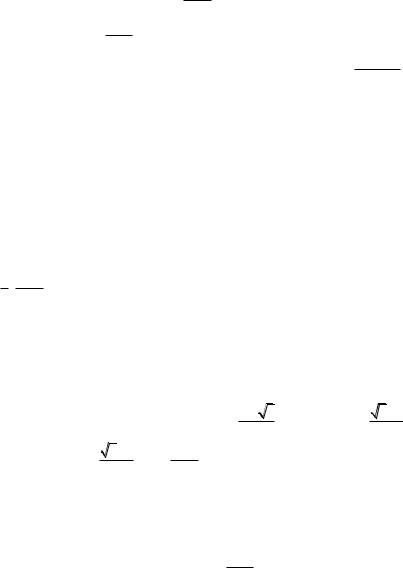
Шаг 1. Определи x1 и x2 по формуле: x1 |
b a |
x2 |
b a |
и вычислить f(x1) и f(x2). |
|
|
|||
2 |
2 |
|
||
Шаг 2. Сравнить f(x1) и f(x2). Если f(x1)≤f(x2), то перейти к отрезку [a,x2], иначе – к отрезку [x1,b].
Шаг 3. Найти достигнутую точность n |
b a |
. Если n , то завершить поиск x* |
|||
2 |
|||||
|
|
|
|
||
Шаг 4. Положить x* x |
a b |
, f * f (x) |
|
||
2 |
|
||||
|
|
|
|
||
Число итераций метода дихотомии определяется неравенством
n log |
b a |
|
|
2 |
2 |
|
15.Метод деления отрезка пополам.
Метод относится к последовательным методам и позволяет исключить на каждом шаге (итерации) метода в точности половину текущего отрезка локализации [a; b]. Для проведения экспериментов выбирают три точки 1, 2, 3 ( 1 < 2 < 3), равномерно расположенные на отрезке локализации [a, b]. После обработки результатов экспериментов( 1), ( 2), ( 3) получается новый отрезок локализации: [a, x1] или [x1, x2] или [x2, b]. На любом из трех возможных новых отрезков локализации лежит в середине отрезков точка из предыдущих экспериментов. Поэтому, если заданная точность не достигнута, то для повторения процесса нужно уже только два эксперимента, а не три, как на первом шаге (итерации) метода. Общее число экспериментов N 2k 1 . Гарантированная точность:
гарант
1 2
( |
b a |
) |
|
|
k |
||
|
2 |
|
|
|
|
|
|
.
16.Метод золотого сечения.
Это метод, при котором рассматривается такое симметричное положение точек x1 и x2, при котором одна из них становится пробной точкой на новом отрезке, полученном после исключения части исходного отрезка. Использование таких точек позволяет на каждой итерации метода, кроме первой, ограничиться определением только одного значения f(x).
Шаг1. Определить x1 и x2 по формуле: x1 a |
3 |
5 |
(b a) |
x2 a |
5 1 |
(b |
a) . Вычислить |
|||||
2 |
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
f(x1) и f(x2). Положить |
5 1 |
, n |
b a |
. |
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Шаг 2. Проверка окончания поиска: если n |
перейти к шагу 3, иначе – к шагу 4. |
|||||||||||
Шаг 3. Переход к новому отрезку и новым пробным точкам. Если f(x1)≤f(x2), то b=x2, x2=x1, f(x2)=f(x1), x1=b-τ(b-a) и вычислить f(x1), иначе – a=x1, x1=x2, f(x1)=f(x2), x2=b-τ(b-a) и вычислить f(x2). Положив n , перейти к шагу 2.
Шаг 4. Окончание поиска: положить |
x* x |
a b |
, f * f (x) |
|
2 |
||||
|
|
|
Процесс продолжается, пока заданная точность не будет достигнута. В качестве приближенного решения выдается середина последнего отрезка локализации и значение функции в этой точке. Гарантированная точность этого решения составляет половину длины этого отрезка локализации.
17.Метод чисел Фибоначчи.
Числа Фибоначчи: F0 1, F1 1, Fk Fk 1 Fk 2 .
В методе чисел Фибоначчи имеющийся отрезок локализации уменьшается на основе двух экспериментов в точка x1,x2 на отрезке локализации [a,b] симметричных относительно середины этого отрезка. В начале каждая из этих двух точек делит отрезок на две неравные части в пропорции пары чисел Фибоначчи. Формулы, определяющие точки:
x a |
FN 2 |
(b a) |
x a |
FN 1 |
(b a) |
. Точность решения |
расчет |
|
1 |
( |
b a |
) |
1 |
FN |
|
2 |
FN |
|
|
2 |
|
FN |
2 |
||
|
|
|
|
|
|
|
||||||
18.Метод касательных.
Если на концах отрезка [ , ] производная ′ ( ) имеет разные знаки, т.е. ′ ( ) ′ ( ) < 0, и она непрерывна, то на интервале ( , ) найдется точка, в которой ′ ( ) обращается в ноль. То что′ ( ) < 0 и ′ ( ) > 0 означает, что касательные проведенные к функции ( ) в точках ( , ( )) и ( ,( )) пересекаются в точке ( ′ , ( ′ )), где [ , ].
Знак производной ′ ( ) в точке ′, позволяет уменьшить отрезок локализации [ , ] до [ , ′] или
4

[ ′, ], также как в методе средней точки. Теперь выведем формулы определения точки ′. Уравнение касательной к ( ) в точке ( , ( )) = ( ) + ′( )( − ) Уравнение касательной к ( ) в точке( , ( )) = ( ) + ′( )( − ). Точка пересечения касательных ( ′ , ( ′ )), это = ( ) +
′( )( ′ − ) = ( ′ ) = ( ) + ′ ( )( ′ − ) = отсюда 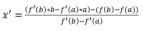
19.Метод средней точки.
Если определение производной ′ ( ) не представляет затруднений, то в процедуре локализации отрезка неопределенности в методе дихотомии вычисление двух значение ( ) вблизи середины очередного отрезка неопределенности можно заменить вычислением одного значения ′ ( ) в его
средней точке x |
a b |
|
|
2 |
|
|
|
|
|
|
|
В самом деле, если |
f '(x ) >0 означает, то |
x |
лежит на участке монотонного возрастания f(x), |
поэтому x*< x и точка минимума принадлежит отрезку [a, x ]. При f '(x ) <0 имеем противоположную ситуацию и переходим к отрезку [ x ,b]. Равенство ′ ( ′) = 0 означает, что точка минимума найдена точно x* = x . Такой способ уменьшения отрезка локализации требует на каждой итерации только одно вычисление ′ ( ) и уменьшает отрезок локализации точно вдвое.
Шаг 1. Положить x |
a b |
. Вычислить f '(x ) . |
|
|
2 |
|
|||
|
|
|
|
|
Шаг 2. Проверка окончания поиска: если | f '(x ) |≤ε, то положить x* x, |
f * f (x) и завершить |
|||
поиска, иначе перейти к шагу 3. |
|
|
||
Шаг 3. Сравнить f '(x ) с 0: если |
f '(x ) >0, то продолжить поиск на отрезке [a, x ]б иначе на отрезке |
|||
[ x ,b]. Перейти к шагу 1. |
|
|
|
|
20.Метод хорд.
Равенство ′ ( ) = 0 является необходимым и достаточным условием глобального минимума выпуклой дифференцируемой функции ( ). Если на концах отрезка локализации [ , ] производная ′ ( ) имеет разные знаки, т.е. ′ ( ) ′ ( ) < 0, и она непрерывна, то на интервале [ ,] найдется точка, в которой ′ ( ) обращается в нуль. Этом **точки минимума ( ) на отрезке [ ,] эквивалентен решению уравнения ′ ( ) = 0, [ , ].
Метод хорд состоит в исключении отрезков путем определения точки x - пересечения с осью Ox
хорды графика функции F(x) на [a,b]. Полагая F(x)=f ′ (x): x a |
|||
|
|
|
f '( |
|
|
f '(a) |
|
Шаг 1. |
Найти x a |
|
(a b) . Вычислить f '(x) . |
f '(a) f '(b) |
|||
Шаг 2. |
Проверка окончания поиска: если | f '(x) |≤ε, то положить |
||
f '(a) a) f
x*
(a b) '(b)
x, f * f (x) и завершить
поиска, иначе перейти к шагу 3.
Шаг 3. Переход к новому отрезку. Если a x, f '(a) f '(x) . Перейти к шагу 1.
f
'(x)
>0, то положить
b x, f '(b)
f
'(x)
, иначе положить
21.Метод Ньютона.
( ) – дважды дифференцируемая функция, причем ′′( ) > 0 на [ , ] (т.е. ( ) выпуклая функция). Уравнение касательной к функции ( ) в точке : = ( ) + ′( )( − ). В качестве следующего приближения +1 берется аргумент когда = 0. Поэтому
y F (xk ) F '(xk )(xk 1 xk )
xk 1 |
xk |
f '(xk ) |
|
f "(xk ) |
|||
|
|
Вычисления производятся до тех пор, пока не выполнится неравенство | f '(xk ) |≤ε, после чего полагают x* xk , f * f (xk ) . Метод Ньютона имеет локальную сходимость. Достаточным условием монотонности сходимости метода Ньютона является постоянство в диапазоне x [x*, x0 ] знака производной f '''(x) и совпадение его со знаком f '(x0 ) .
22. Многомерная безусловная оптимизация. Постановка задачи.
Задача, требующая нахождения оптимального значения функции m переменных , f x f (x1, x2 , , xm ), называется задачей многомерной оптимизации.
5

Рассмотрим задачу оптимизации: найти минимум функции f (x) n -мерного аргумента x , компоненты которого удовлетворяют системе ограничений в виде уравнений
Hk x = 0, k =1, 2,..., m или неравенств g j (x) 0, j m 1,..., s. Такая задача
называется задачей условной оптимизации. Если задача не содержит ограничения и рассматривается на всем пространстве, то это задача безусловной оптимизации.
23.Поиск по образцу.
Выберем точку начального приближения x0, вычислим в ней значение f(x0). Затем построим n- мерный куб с центром в этой точке и ребрами длиной 2h. Множество вершит этого куба вместе с точкой x0 составляют образец (шаблон). Вычислив значения функции в вершинах куба, выберем в качество новой базовой точки ту из вершин, в которой значение функции меньше f(x0) и повторим процедуру выбора следующей базовой точки и построения образца. Если точки не оказалось, то оставим прежнюю базовую точку и построим образец с уменьшенной длиной ребер куба.
24.Метод конфигураций.
Метод конфигураций представляет собой комбинация исследования окрестности базовой точки с циклическим изменением переменных и ускоряющего перемещения в направлении убывая в следующую базовую точку. Алгоритм содержит две основные процедуры на каждом шаге:
1)Исследование окрестности базовой точки x0 с целью нахождения направления спуска. (поиск направления, в котором значения функции последующей точки будет меньше предыдущего).
2)Ускоряющееся перемещение в направлении спуска. (перемещение на заданный ускоренный шаг и присвоение новой базисной точки, если ускорение оказалось удачным. Иначе происходит возврат в предыдущую точку и уменьшение шага вдвое).
25.Метод симплекса.
Симплекс – простейший выпуклый многогранник с n+1 вершин. Суть метода состоит как и в предыдущем нахождения значения функции в вершинах. После этого точку наибольшего значения функции отражают относительно плоскости и строят новый симплекс, при этом уменьшая длину ребер симплекса. Условием прекращения поиска является муеьшение размеров симплекса (ребра) до выбранного значения.
26.Метод циклического покоординатного спуска.
6

27. Градиент. Градиент и направление роста целевой функции. Градиентные методы.
Градиентом f (x) непрерывно дифференцируемой функции f(x) в точке x называется вектор-
столбец, элементами которого являются частные производные первого порядка, вычисленные в данной точке.
f (x)
|
x1 |
|
|
|
|
|
f (x) |
|
|
x2 |
|
f (x) |
|
|
|
... |
|
|
|
|
|
f (x) |
|
|
xn |
|
|
|
|
Градиент функции направлен по нормали к поверхности уровня, т.е. перпендикулярно к касательной плоскости, проведенной в точке x, в сторону наибольшего возрастания функции в данной точке.
Антиградиент – вектор, равный по модулю вектору градиента, но противоположный по направлению. Он указывает в сторону наибольшего убывания функции в данной точке.
28.Градиентный метод с постоянным шагом.
Градиентный метод с постоянным параметром шага предполагает, что  =
=  , где
, где 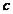 - постоянная величина, например
- постоянная величина, например 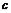 = 1. Тогда шаг будет равен длине градиента в текущей точке и направлен в сторону возрастания функции.
= 1. Тогда шаг будет равен длине градиента в текущей точке и направлен в сторону возрастания функции.
По мере приближения к стационарной точке (если функция вообще имеет стационарную точку локального максимума) длина шага будет уменьшаться и процесс приближения будет замедляться.
29.Градиентный метод с дроблением шага.
Градиентный метод с дроблением шага. Параметр 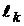 на каждой итерации вычисляется по формуле
на каждой итерации вычисляется по формуле
,
в результате чего длина шага не зависит от длины градиента и остается постоянной, равной 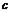 . Кроме того, выбирая знак параметра
. Кроме того, выбирая знак параметра  , можно выбирать направление движения - к максимуму (
, можно выбирать направление движения - к максимуму (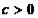 ) или к минимуму
) или к минимуму
7

(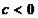 ). Однако может случиться так: приблизившись к стационарной точке, мы сделаем очередной шаг,
). Однако может случиться так: приблизившись к стационарной точке, мы сделаем очередной шаг,
который окажется слишком большим. Обнаружится, что 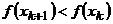 (предполагается, что мы ищем максимум), т.е. полученный результат хуже предыдущего. Это значит, что мы вошли в область стационарной точки, необходимо уменьшить шаг. В соответствии с этим параметр
(предполагается, что мы ищем максимум), т.е. полученный результат хуже предыдущего. Это значит, что мы вошли в область стационарной точки, необходимо уменьшить шаг. В соответствии с этим параметр 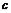 уменьшается, например, в 2 раза. И процесс продолжается. Так будет происходить до тех пор, пока длина шага не станет достаточно малой. Этот метод прост, но его существенный недостаток состоит в том, что выбор параметра
уменьшается, например, в 2 раза. И процесс продолжается. Так будет происходить до тех пор, пока длина шага не станет достаточно малой. Этот метод прост, но его существенный недостаток состоит в том, что выбор параметра 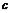 приходится делать субъективно.
приходится делать субъективно.
30.Стандартная задача линейного программирования.
Задачей линейного программирования называется задача, которая состоит в определении
|
F |
n |
максимального (минимального) значения функции |
c j |
|
|
|
j 1 |
n |
|
|
aij x j bi (i 1,..k) |
|
|
j 1 |
|
|
n |
|
|
aij x j bi (i k 1,..m) |
|
|
j 1 |
|
|
x j 0 ( j 1,...l; l n) |
|
|
n
Функция F c j x j называется целевой функцией задачи,
j 1
x j |
при выполнении условий: |
а условия – ограничениями данной
задачи.
31.Каноническая задача линейного программирования.
Канонической задачей линейного программирования называется задача, которая состоит в определении максимального значения функции при выполнении двух последних условий, где k=0, l=n.
32.Способы перехода от ограничений неравенств к равенствам.
Переход от ограничений-неравенств к ограничениям-равенствам производится путем введения дополнительных неотрицательных переменных. Таким образом, ограничение-неравенство
a |
x |
a |
x |
... a |
x £b |
|
i1 |
1 |
i 2 |
2 |
in |
n |
i |
33.Способы перехода от ограничений равенств к неравенствам.
Переход от равенства к неравенствам осуществляется путем преобразования равенства в два неравенства.
X |
K |
, X |
K |
X |
K |
X |
K |
, X |
0 |
|
|
|
|
|
K |
34.Базисное решение задачи ЛП.
35.Связь базисных решений с угловыми точками (вершинами) множества допустимых решений
(ОДР).
Теорема. Любое опорное решение является угловой точкой области допустимых решений. Теорема. Любая угловая точка области допустимых решений является опорным решением.
36.Графический метод решения задачи ЛП.
8

37.Симплекс-метод решения задачи ЛП.
Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве.
Сущность метода: построение базисных решений, на которых монотонно убывает линейный функционал, до ситуации, когда выполняются необходимые условия локальной оптимальности.
Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.
38. Критерий оптимальности решения в симплекс-методе. Условия единственности и множественности оптимального решения.
39. Метод искусственных переменных. Критерий отсутствия оптимального решения исходной задачи.
Идея использования искусственных переменных предполагает включение неотрицательных переменных в левую часть каждого из уравнений, в которых не содержится очевидных начальных базисных переменных (когда неравенство имеет знак ≥ или задано в виде равенства). Эти дополнительно вводимые переменные выполняют ту же роль, что и остаточные переменные. Но так как искусственные переменные не имеют отношения к поставленной задаче (отсюда их название - искусственные), то их введение допустимо только в том случае, если симплекс метод будет обеспечивать получение оптимального решения, в котором все искусственные переменные будут равны 0, то есть эти переменные следует использовать только для стартовой точки, причем итерационный метод оптимизации должен "вынуждать" эти переменные принимать нулевые значения в конечном оптимальном решении, обеспечивая допустимость оптимума.
9

Если в оптимальном решение Т-задачи все искусственные переменные равны 0, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи.
Если имеется оптимальное решение Т-задачи, в котором хотя бы одна из искусственных переменных отлична от 0, то система ограничений исходной задачи несовместна.
Если максимум Т-функции равен бесконечности, то исходная задача неразрешима (либо система несовместна, либо максимум неограничен).
Другое:
10
