Контрольная работа по Математике Вариант 1 / Контрольная работа Вариант 1 (1 курс ФЗО)
.docКонтрольная работа 1
Задание 1
Даны координаты
вершин пирамиды. Найти: 1) длину ребер
![]() и
и
![]() ;
2) угол между ребрами
и
;
2) угол между ребрами
и
![]() ;
3) площадь грани
;
3) площадь грани
![]() ;
4) объем пирамиды; 5) уравнения прямой
;
6) уравнение плоскости
;
7) угол между ребром
;
4) объем пирамиды; 5) уравнения прямой
;
6) уравнение плоскости
;
7) угол между ребром
![]() и
гранью
;
8) уравнения
высоты, опущенной из вершины
и
гранью
;
8) уравнения
высоты, опущенной из вершины
![]() на
грань
.
на
грань
.
(6; 6; 5) |
(4; 9; 5) |
(4; 6; 11) |
(6; 9; 3) |
Решение
1)Найдем длину
ребра
![]()

2) Найдем угол между
ребрами
![]() и
через скалярное произведение
и
через скалярное произведение
Угол найдем черед скалярное произведение

3) Найдем площадь
грани
![]()
Площадь грани, построенного на векторах равна половине длины векторного произведения векторов на которых построена данная грань

4) Найдем объем пирамиды
Объём пирамиды,
построенный на векторах равен
![]() модуля смешанного произведения векторов
на которых построена данная пирамида
модуля смешанного произведения векторов
на которых построена данная пирамида

5) Составим уравнения прямой
![]()
6) Найдем уравнение плоскости

7) Найдем угол
между ребром
![]() и гранью
и гранью
Нормальный вектор
плоскости
![]() ,
его длина
,
его длина
![]() ,
направляющий вектор ребра
-
,
направляющий вектор ребра
-
![]()

8) уравнения высоты,
опущенной из вершины
![]() на
грань
записывается в виде
на
грань
записывается в виде
![]()
Задание 2
Линия задана
уравнением
![]() в полярной системе координат.
в полярной системе координат.
Требуется:
1. построить линию
по точкам от
![]() до
до
![]() ,
придавая
,
придавая
![]() значения через промежуток
значения через промежуток
![]() ;
;
2. найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;
3. по уравнению в декартовой прямоугольной системе координат определить, какая это линия. Уравнение
![]()
Решение
Построим кривую
по точкам меняя значение параметра
![]() от 0 до
от 0 до
![]() с шагом
с шагом
![]()
Строим таблицу
|
0 |
|
|
|
|
|
|
|
|
1,00 |
1,04 |
1,18 |
1,44 |
2,00 |
3,24 |
6,82 |
26,28 |
|
|
|
|
|
|
|
|
|
|
|
26,28 |
6,82 |
3,24 |
2 |
1,44 |
1,18 |
1,04 |
Строим график
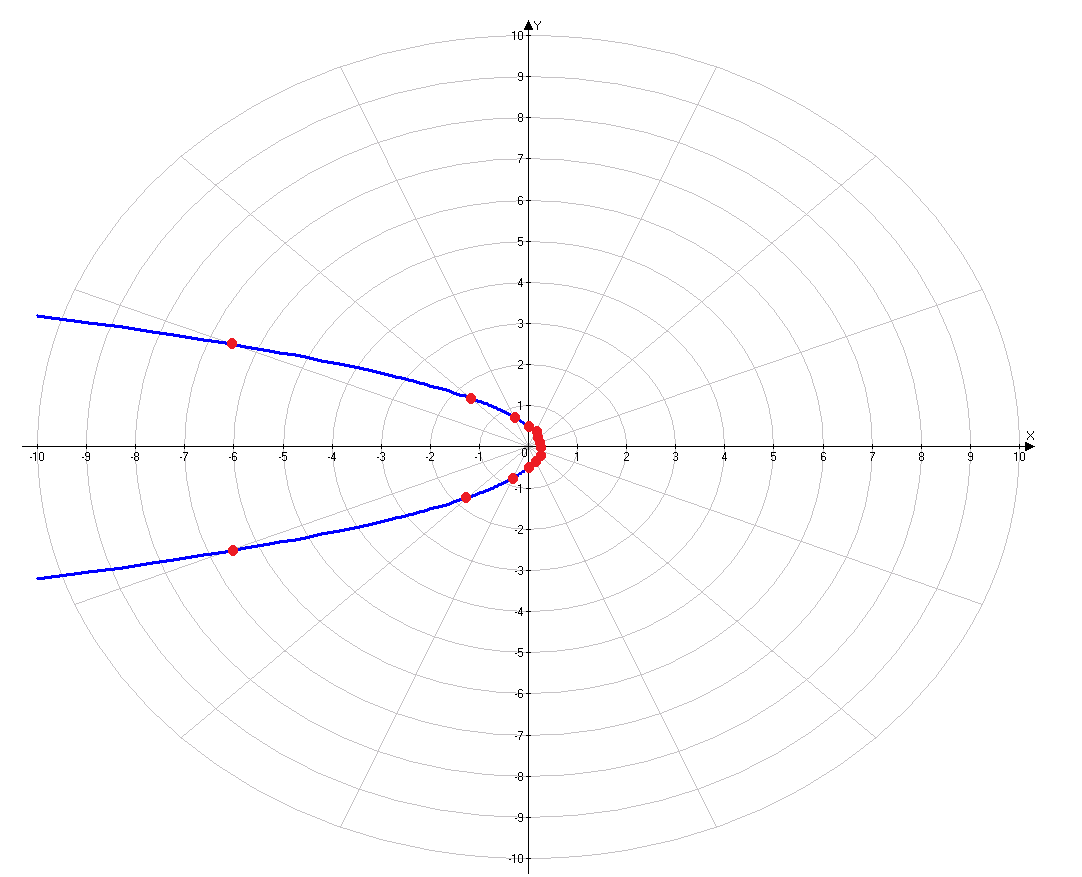

Данная кривая –
парабола с вершиной в точке
![]() ,
параметром
,
параметром
![]() и осью симметрии
и осью симметрии
![]()
Контрольная работа 2
Задание 1
Даны две матрицы![]() .
Найти
.
Найти![]() .
.
 ,
,
 .
.
Решение

Задание 2
Дана система трех линейных уравнений с тремя неизвестными. Требуется: 1) найти ее решение с помощью формул Крамера; 2) записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
![]()
Решение
Метод обратной матрицы
Запишем
систему в виде:

С учетом обозначений система уравнений принимает следующую форму: АХ = B. Умножив обе части уравнения на А-1, получим: Х = А-1B. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1.
∆=1∙(9∙3-(-6∙(-4)))-1∙(3∙3-(-6∙(-2)))+2∙(3∙(-4)-9∙(-2))=18
Так как определитель 18 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения.
Транспонированная матрица
Найдем алгебраические дополнения матрицы AT.
∆1,1=(9∙3-(-4∙(-6)))=3
∆1,2=-(3∙3-(-2∙(-6)))=3
∆1,3=(3∙(-4)-(-2∙9))=6
∆2,1=-(1∙3-(-4∙2))=-11
∆2,2=(1∙3-(-2∙2))=7
∆2,3=-(1∙(-4)-(-2∙1))=2
∆3,1=(1∙(-6)-9∙2)=-24
∆3,2=-(1∙(-6)-3∙2)=12
∆3,3=(1∙9-3∙1)=6
Обратная матрица
Проверим вычисление обратной матрицы

Тогда,

Метод Крамера
Заменим
1-й столбец матрицы А на вектор В. Найдем
определитель полученной матрицы
∆1 =

![]() Заменим
2-й столбец матрицы А на вектор В. Найдем
определитель полученной матрицы
∆2 =
Заменим
2-й столбец матрицы А на вектор В. Найдем
определитель полученной матрицы
∆2 =

![]() Заменим
3-й столбец матрицы А на вектор В. Найдем
определитель полученной матрицы
Заменим
3-й столбец матрицы А на вектор В. Найдем
определитель полученной матрицы
∆3 =

![]()
Задание 3
Определить собственные значения и собственные векторы матрицы третьего порядка.

Решение
Найдем собственные значения и собственные векторы. Для этого составим характеристический многочлен

Получили собственные значения, найдем собственные значения
При
![]() получаем
получаем
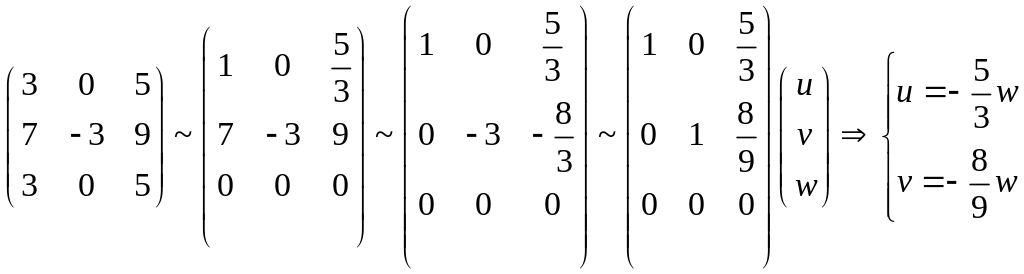
При
![]() получаем первый собственный вектор
получаем первый собственный вектор
![]()
При
![]() получаем
получаем

При
![]() получаем второй собственный вектор
получаем второй собственный вектор
![]()
При
![]() получаем
получаем

При
![]() получаем третий собственный вектор
получаем третий собственный вектор
![]()
Задание 4
Дано комплексное
число z.
Требуется: 1) записать число z
в алгебраической и тригонометрической
формах; 2) найти все корни уравнения![]() .
.
![]()
Решение

Так как
![]() ,
поэтому
,
поэтому
![]() лежит во второй четверти, значит,
лежит во второй четверти, значит,
![]() и
и
![]() ,
значит,
,
значит,
![]()
![]()
Так как
![]() ,
поэтому
,
поэтому
![]() лежит в четвертой четверти, значит,
лежит в четвертой четверти, значит,
![]() и
и
![]() ,
значит,
,
значит,
![]()
Для вычисления кубического корня применим формулу Муавра

Контрольная работа 3
Задание 1
Найти пределы функций, не пользуясь правилом Лопиталя.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
Решение
1)

2)
3)![]()
4)
 .
.
Задание 2
Задана функция![]() .
Найти точки разрыва функции, если они
существуют. Сделать
чертеж.
.
Найти точки разрыва функции, если они
существуют. Сделать
чертеж.

Решение
Возможные точки
разрыва для функции есть
![]()
Найдем односторонние пределы

Тогда, получаем,
что
![]() ,
значит, функция непрерывна в точке 2
,
значит, функция непрерывна в точке 2
Так как![]() и оба предела являются конечными, значит,
и оба предела являются конечными, значит,
![]() - точка разрыва первого рода
- точка разрыва первого рода

Задание 3
Найти производные первого порядка данных функций.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() .
.
Решение
1)

2)
3)
4)Применим логарифмическое дифференцирование
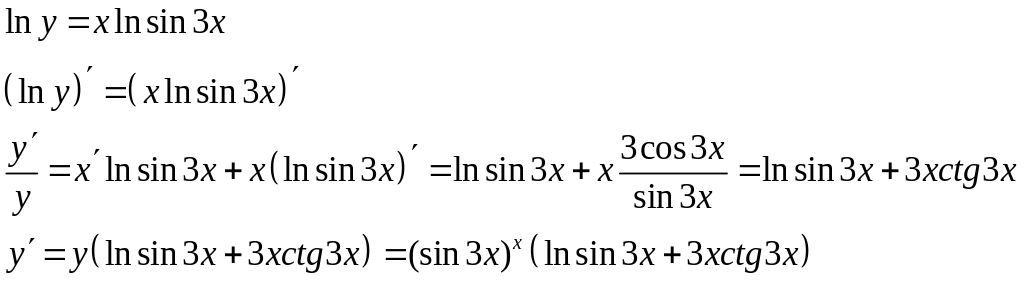
5)Возьмем производную от обеих частей равенства

Задание 4
Найти
![]() для заданных функций: 1)
для заданных функций: 1)
![]() 2)
2)
![]()
Решение
1)Найдем первую производную

Найдем вторую производную
 2)
Найдем первую производную
2)
Найдем первую производную

Найдем вторую производную
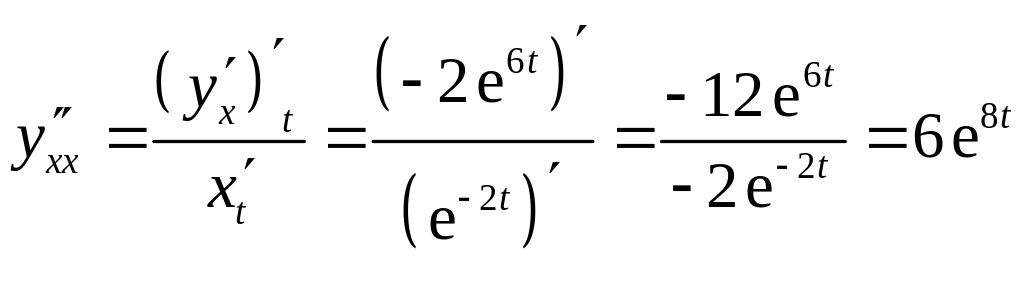
Контрольная работа 4
Задание 1
Найти наибольшее
и наименьшее значения функции
![]() на отрезке [0;4].
на отрезке [0;4].
Решение
Так как свои наименьшее и наибольшее значения непрерывная на отрезке функция может принимать либо на концах этого отрезка, либо в точках экстремума, входящих в этот отрезок, то находим значения исследуемой функции во всех этих точках и среди них выбираем наибольшее и наименьшее значения:

![]() при
при
![]()
![]()
![]()
![]() .
.
Выбираем наибольшее значение функции из найденных чисел – это 1. Теперь наименьшее – это 0
Задание 2
Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.
|
|
Решение
А)
1) Область определения функции
![]()
2) Найдем точки пересечения с осью OX

, значит точка
пересечения с осью OX
-
![]()
3)
Так как
![]() ,
данная функция не является ни нечетной,
ни четной
,
данная функция не является ни нечетной,
ни четной
Функция не является периодической
4)
![]() являются точками разрыва
являются точками разрыва
5) - вертикальные асимптоты
Найдем наклонные
 ,
,
![]() ,
значит
- наклонная асимптота.
,
значит
- наклонная асимптота.
6) Найдем экстремумы функции и интервалы монотонности

![]()

Корней нет
Изобразим на координатной прямой

Значит
![]() возрастает на всей области определения.
Точек экстремума нет
возрастает на всей области определения.
Точек экстремума нет
7) Найти точки перегиба и характеры выпуклости


Изобразим на координатной прямой

Значит
выпукла
вниз при
![]() и
выпукла вверх при
и
выпукла вверх при
![]() .
Точка
.
Точка
![]() - точка перегиба.
- точка перегиба.
8)

Б) 1. Предварительный анализ
1)Области определения и значения f(x)
Область
определения функции
![]() ,
область значении найдем после анализа
функции
,
область значении найдем после анализа
функции
2)Интервалы непрерывности и точки разрыва
Функция является произведением двух непрерывных функции, значит функция является непрерывной на всей области определения, соответственно, точек разрыва нет
3)Вертикальные асимптоты
Так как точек разрыва нет, то и вертикальных асимптот нет
4) Характерные точки графика
Характерных точек графика нет
5)Четность, нечетность функции
![]()
Так как
![]() и
и
![]() ,
данная функция не является ни четной,
ни нечетной. Также она не является
периодической
,
данная функция не является ни четной,
ни нечетной. Также она не является
периодической
2. Наклонные и горизонтальные асимптоты
![]() ,
,
 ,
значит
,
значит
![]() - наклонная асимптота при
- наклонная асимптота при
![]()
![]() ,
значит при
,
значит при
![]() наклонных асимптот нет
наклонных асимптот нет
3. Исследование экстремумов функции
1)интервалы функции 2)точки экстремумов 3) экстремальные значения функции
![]()

Изобразим на координатной прямой

Значит,
возрастает
при
![]() ,
убывает
при
,
убывает
при
![]() .
.
![]() - точка минимума
- точка минимума
5. Исследование на выпуклость и вогнутость 1)интервалы 2)точки перегиба функции
![]()
![]()
![]()
Изобразим на координатной прямой

Значит
выпукла
вверх при
![]() ,
выпукла
вниз при
,
выпукла
вниз при
![]()
![]() -
точка перегиба
-
точка перегиба
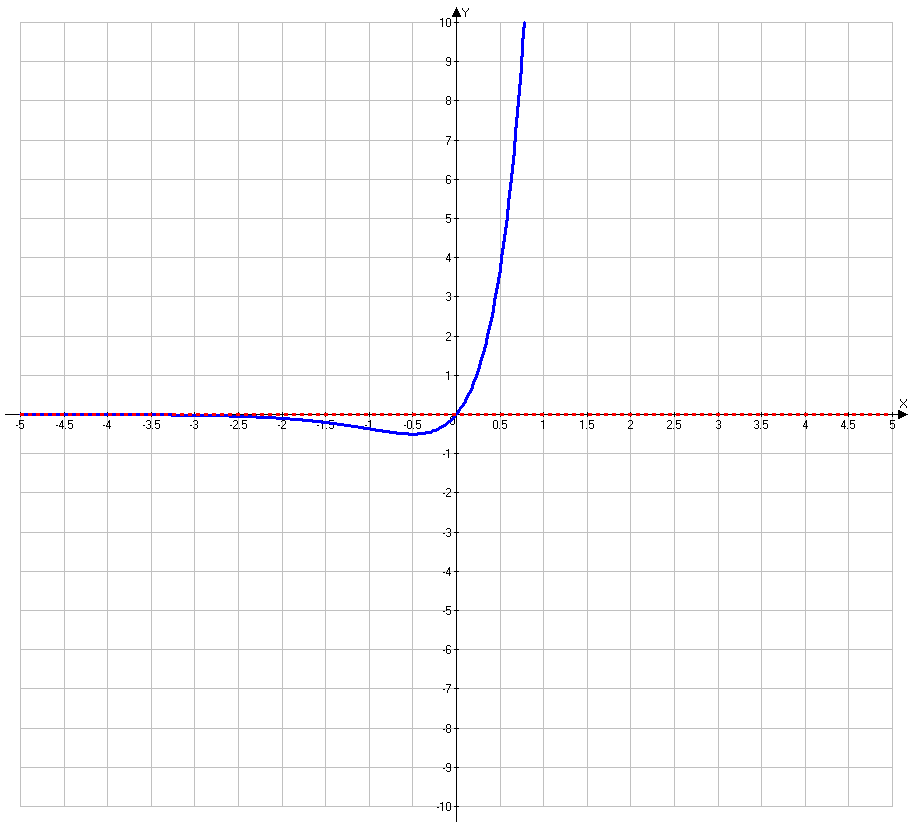
6. Построение графика
Контрольная работа 5
Задание 1
Найти неопределенные интегралы. В п. 1) и 2) результаты проверить дифференцированием.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]()
Решение
1)Воспользуемся внесением под знак дифференциала
![]() Проверим
дифференцированием
Проверим
дифференцированием

2)Применим метод интегрирования по частям
 Проверим
дифференцированием
Проверим
дифференцированием
 3)Разложим
подынтегральное выражение на сумму
дробей
3)Разложим
подынтегральное выражение на сумму
дробей

Тогда,
![]()
4)Сделаем замену переменной

Задание 2
Вычислить несобственный интеграл или доказать его расходимость.
![]()
Решение

Задание 3
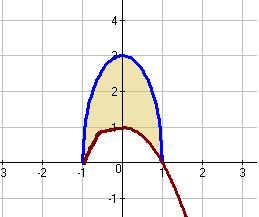
Вычислить (с точностью до двух знаков после запятой) объем тела, полученного вращением фигуры вокруг указанной оси координат.
![]()
Решение
Сделаем чертеж тела вращения