makry_zachet

В слабом магнитном поле 2 min, 2 направления оси спонтанной намаг - ти

H < M(β − β )

π

H ≥ M(β − β )−1 min, θm = 2

Всильном магнитном поле остается одна ось намагниченности M ↑↑ H

Вотсутствии МП имеются 2 направления спонт наманг. отвечающие значению sinθ = 0, это 0 и π. Те два возможных направления вектора спонтанной намагничиваемости, вдоль оси легкого намаг, это указывает на то, что ферромагнетик может разбиваться на области с ращными векторами спонтанной намагничиваемости - на домены.

Домены - области с различными значениями спонтанной намагничиваемости.

Рассм. случай Hx = 0, Hz = H β < β

F = 12 (β − β )M2sin2θ − McosθH, перейдем к cos (... не зав от направл)

F = − 12 (β − β )M2 cos2 θ − McosθH =

Ищем минимум: 0 ≤ θ ≤ π

H

M(β − β ) < 1 (картинка справа) Возникает 2 значения угла при котором возникает мин. θm = 0, θm = π при нуле более энергетически выгодное положение, а в пи метастабильное

H

M(β − β ) ≥ 1 только одно значение

минимума θm = 0, и только одна ориентация магнитного момента

Если магнитное поле ориентировано вдоль Oz то вектор спонтанной намагниченности может принимать ориентацию по волю и против поля. В сильном магнитном поле, вектор M направлен только по полю (энергетически выгодно)

В отсутствии магнитного поля имеются два направления одинаково энергетически выгодные и отвечающие направлению спонтанной намагниченности вдоль оси легкого намагничивания.

Замечания: Без ограничения общности, считали что Hx , Hz > 0. Действительно, всегда можно выбрать положительные направления осей z и x в направлении магнитного поля.

Рассм выражение в общем случае, будем искать минимум β < β

находим sin подставляем в предыдущее выражение и получаем ответ:

Hx2/3 + Hz2/3 = ((β − β )M)2/3

Нарисуем график этого уравнения на плоскости Hz , Hx

Эта картинка есть значение магнитного поля на две области. Внутри этой области возможны два состояния отвечающие минимуму свободной энергии, и соотвественно две возможные ориентации вектора спонтанной намагниченности. А в облости вне фигуры возможно только одно

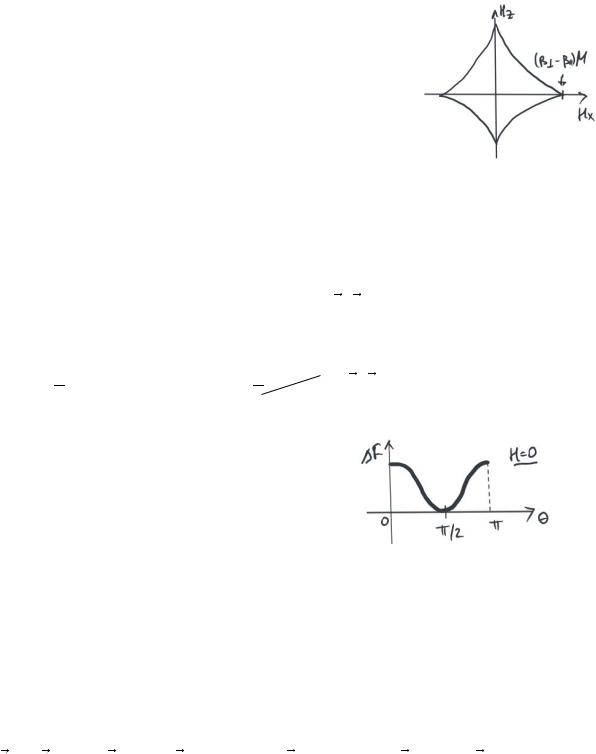
состояние отвечающее мин свободной энергии, соотвественно одна ориент спонтанной намагнич.

Поведение вектора спонтанной намагниченности в зависимости от значений вектора магнитного поля

Случай когда имеется плоскость легкого намагничивания: β > β

β M2 sin2 θ = β M2 − β M2 cos2 θ тогда получаем:

F= 12 (β − β )M2 cos2 θ + 12 β M2 − MH

Вотсутсвии магнитного поля H = 0

минимум будет: θ = π2

Те вектор спонтанной намагниченности будет ориентирован в плоскости лекого намагничивания.

Доменная структура

Возможны различные ориентации вектора спонтанной намагничености. В отсутсвии МП в случае одноосного кристалла имеется два направления вектора Спонт намагн. Поэтому, возможна ситуация когда ферромагнетик разбивается на области в которых вектор спонт намг имеет различную ориентацию

B = H + 4πM div B = 0, div H = −4πdiv M, rot H = 0, (нет

сторонних токов)

Уравнения похожи на уравнения электростатики. ГУ Hl, и Bn должны быть не прерывны.

Вектор M отличен от нуля внутри ферромаг -ка и равен нулю вне его. Возникает скачок на границе,

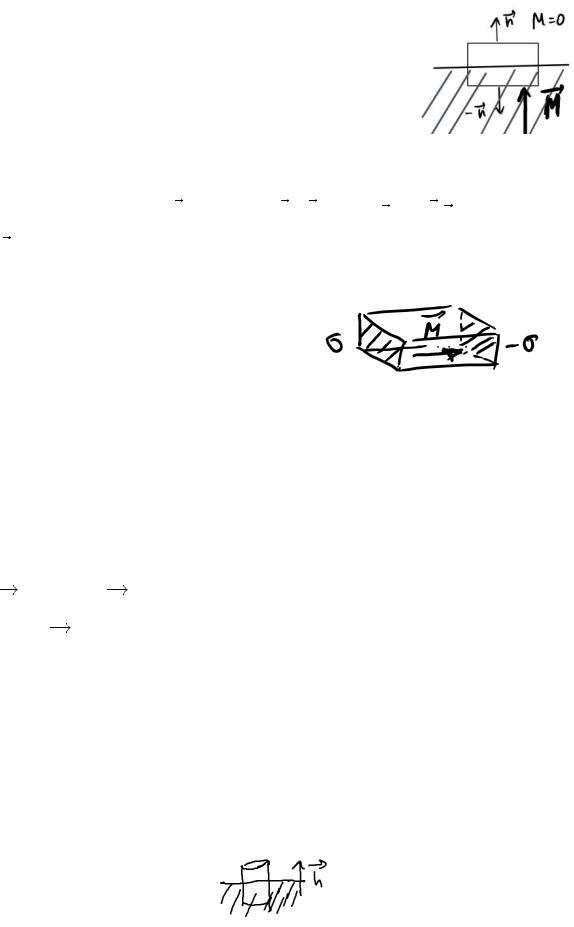
можем выслить чему равняется плотность эквавал “магнитных зарядов”.

σS = ∫ ρdV = − ∫ div MdV = − ∫ Mdf = −0 n − (Mn)S = MnS,

где n− внешняя нормаль к поверхности среды, S−площатдь повти

Если имеется вектор спонтанной намаг, который испытвает скачок на границе ферромагнетика , то мы получаем задачу типо электрост - кой, в которой на повти образца расположены поверхностные заряды

Штрих это заряды. Важно что напртивопложенных границах знаки “магнитных зарядов” противополжены. те эта область ферромагнетика, выступает как магнитный конденсатор, магнитный диполь который пораждает магнитное поле в такой конфигурации. Поэтому эта задача нахождения МП в случае ферромаг-ка с заданной спонатнной намагниченностью, сводится просто к задаче о конденсаторе с заданной плотностью поверхностных зарядах.

divH = −4πdivM = 4πρ, где

ρ = −divM

Теперь, если мы рассмотрим границу ферромагнетика: есть намагниченность М

рассмотрим какая плотность эквивалентных зарядов соответствует такой намагниченности

Рассмотрим некоторый объем, который охватывает границу (цилиндрическую область)

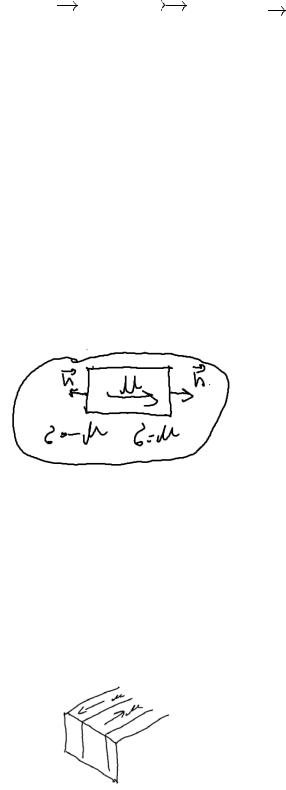
∫ pdV = ∫ σdf = − ∫ dV divM = − ∫ d f M = − ∫ df n (Мвн-М) =

[Мвнешнее стремится к нулю]

= ∫ Mndf, Мn-проекция вектора намагниченности на внешнюю нормаль границы ферромагнетика.

Поскольку интегрирование по произвольной площадке и за счет скачка намагниченности на границе ферромагнетика мы получаем при таком описании эквивалентную плотность зарядов, которая характеризуется поверхностной плотностью Mn

σ = Mn.

Поэтому если мы берем какую-то область в которой имеется намагниченность ,то внешние нормали такие и мы получаем плотность эквивалентных зарядов М и -М.

То есть ферромагнетик который испытывает на границе скачок намагниченность эквивалентна магнитному диполю с магнитными зарядами М и -М.

Намагниченность может иметь два значения +-М, и оба значения включают минимум энергий, то тогда возникает возможность разбиться ферромагнетику на области. (не всегда так, как на рисунке)

Почему такая ситуация возможна? Потому что за счет разбиения ферромагнетика на домены, происходит уменьшение вклада в энергию за счет МП внутри ферромагнетика. Ферромагнитные состояния возникают из-за выигрыша за счет возникновения спонтанной намагниченности, связанной с

обменными взаимодействиями. Обменные взаимодействия приводят к тому, что у нас понижается энергия и одновременно возникает спонтанная намагниченность. При возникновении спонтанной намагниченности возникает магнитное поле внутри ферромагнетика и тем самым к выигрышу добавляется проигрыш в энергии за счет МП. Поэтому если реализуется разбиение на домены, то такой процесс частично компенсирует тот проигрыш в энергии, который связан с энергией МП. Если у нас области со значениями намагниченности , которые ориентируют таким образом, как противоположные(рис.), то энергия МП уменьшается и это состояние оказывается энергетически более выгодным, чем состояние, когда нет разбиения на домены.

7. Электродинамика сверхпроводников. Эффект Мейсснера. Сверхпроводящий шар и цилиндр в однородном магнитном поле (внешняя задача).

Магнитный поток через сверхпроводящее кольцо. Фазовый переход в сверхпроводнике. Критическое магнитное поле.

Электродинамика сверхпроводников

Поскольку сверхпроводящие состояния относятся к состояниям которые характерны для металлов, то все что было сформулировано для Ме остается справедливым.

Электрическое поле внутри равно 0, а на границе тангенциально составляющая ЭП равна 0, поэтому ЭП должно быть направлено по нормали к поверхности сверхпроводника.

Эффект Мейснера:

Магнитное поле внутри сверхпроводника равно 0. (МП не проникает внутрь сверхпрводника)

Будем считать, что имеем дело со сверхпроводниками первого рода.

Намагниченность внутри сверхпроводника отсутствует.

Bin = 0, M = 0, Hin = 0

Что касается граничных условий?

Поскольку у нас нормальная компонента МП непрерывна на границе проводника, то на границе сверхпроводника тоже самое. То есть МП вблизи границы параллельно границе сверхпроводника.

Bn S = 0

Что касается тангенциальной составляющей?

[ n H] S = 4cπ i

Здесь МП снаружи проводника, тк внутреннее равно 0.

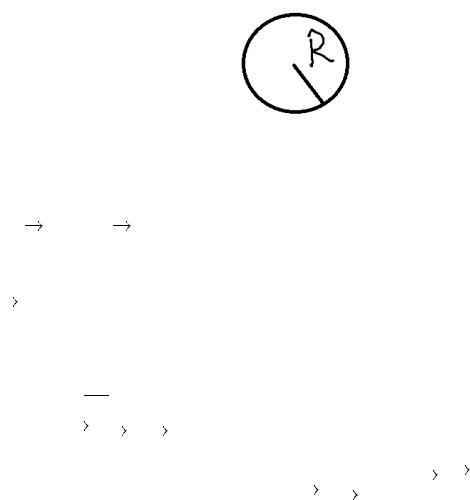
Задача о сверхпроводнике, помещенном во внешнее МП.

Находим распределение МП вне сверхпроводника, опираясь на соответствующие граничные условия и на то, что у сверхпроводника нет намагниченности и напряженности МП. И дальше по найденному нами значению напряженности находим тот поверхностный ток, который возникает в сверх. Благодаря возникновению которого МП внутрь сверхпроводника не проникает.

Рассмотрим задачу о сверхпроводящем шаре, помещенном в однородное МП.

μ = 1

Уравнение Максвелла вне сверхпроводника:

rotH = 0, divH = 0

Нам нужно решить эти уравнения, для этого ведем скалярный потенциал.

H = − ψ, ψ = 0

Граничное условие:

∂ψ

Hn s = 0, ∂r r=R

ψ → − (H0 r ) , r → ∞

неизвестная нам константа, можем найти, используя граничные условия

Нас интересует значение тока, которое возбуждается на поверхности таки образом, чтобы компенсировать проникновение МП внутрь сверхпроводника.

H = − ψ = H0 + R3 H0 + R3 ( r H0 )r (−3) 2 r3 2 r5

Выражение на границе:

r = R, H = 32 H0 − 32 n ( n H0 ) = 32 [ n [H0 n ]]

Вычислим поверхностный ток:

граничное условие

r= R, [ n H] = 4cπ i

i = 4cπ [ n H] = 4cπ 32 [ n H0 ]

Вычислим магнитный момент, который возникает в результате того, что по поверхности сверхпроводника течет такой ток:

M = 21с ∫ dV [F j ] = 21с ∫ dφ sin θdθr2dr [ r j ]

Поскольку ток течет по поверхности, то интеграл по радиальной переменной сразу снимается

Теперь вспомним выражение для скалярного потенциала:

ψ = − ( r H0 ) − R3 ( r H0 )

2 r3

Видим, что в нем уже содержится магнитный момент.

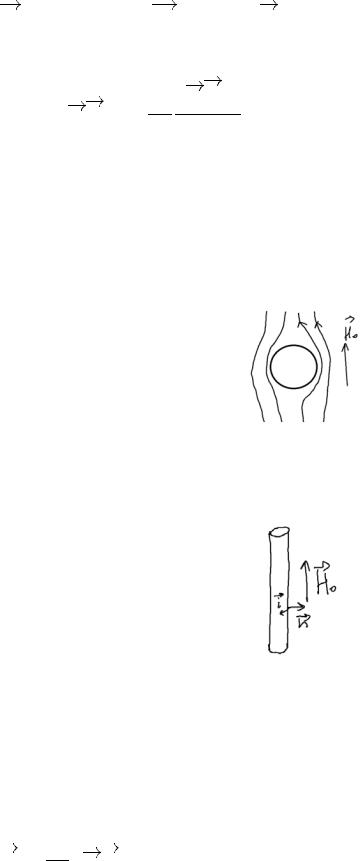
Замечание: Силовые линии МП, которые обтекают шар. Поскольку у нас нормальные компоненты МП на поверхности обращаются в 0, то можно нарисовать как устроены магнитные линии. Соответственно ток возникающий ориентирован так, чтобы компенсировать проникновение МП внутрь сверхпроводника.

Рассмотрим еще один пример, а именно цилиндр сверхпроводящий, помещенный в однородное внешнее МП.

Когда обращаемся к цилиндру в МП, то здесь вопрос о нахождении МП вблизи сверхпроводника не возникает, потому что однородное МП удовлетворяет уравнению, граничным условиям и только тангенциальная компонента отлична от нуля. Поэтому здесь МП остается однородным вплоть до границы сверхпроводника.

Найдем поверхностный ток:

i = 4cπ [ n H0 ]

Поверхностный ток при такой ориентации направлен по часовой стрелке, если