Эк. БИЛЕТ № 1

1. Электрический заряд, его свойства. Закон Кулона. Электрическое поле, напряженность электрического поля, принцип суперпозиции. Напряженность поля точечного заряда и системы зарядов.

Электрический заряд – скалярная величина, определяющая способность тела быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.

Свойства электрического заряда:

1) Это инвариантная величина (т.е. неизменная величина, значение которой не меняется с течением времени)

2) Электрический заряд существует в 2 видах: положительный и отрицательный

3) Это дискретная величина (можно выразить с помощью целых чисел)

4) Выполняется закон сохранения зарядов. В любой изолированной системе алгебраическая сумма зарядов остается неизменной.

Закон Кулона – закон, определяющий силу взаимодействия двух точечных зарядов

(12 означает со стороны первого заряда на второй)

Электрическое поле. Взаимодействие между зарядами осуществляется через поле. Любой электрический заряд изменяет свойства окружающего его пространства – создает электрическое поле. Поле проявляется таким образом, что что помещенный в какую либо его точку пробный заряд (пробный заряд всегда положительный) испытывает действие силы.

( qштрих – пробный заряд,

Е – Напряженность эл. Поля в точке - сила, действующая на пробный заряд

- закон Кулона в полевой форме.

Сила, действующая на пробный заряд не зависит от того, движется он или нет.

Принцип суперпозиции: Напряженность поля системы точечных зарядов равна сумме напряженности отдельных зарядов.

r_{i –} расстояние между q_{i –} и рассматриваемой точкой. Принцип суперпозиции позволяет вычислять напряженность поля любой системы зарядов.

2. Теорема о циркуляции вектора h (в интегральной и дифференциальной формах). Поле в линейном однородном изотропном магнетике. Граничные условия на границе раздела двух магнетиков.

Вектор H.

В магнетиках (Если в магнитное поле внести вещество, то поле изменится. Такое вещество называется магнетиком), помещенных во внешнее магнитное поле, возникают токи намагничивания. Поэтому поле B и его ротор будет определяться не только токами проводимости, но и токами намагничивания

где . Обьединим оба члена с ротором и введем новое, вспомогательное(придуманное) поле

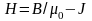. Вектор H часто называется напряженностью магнитного поля. Он представляет собой комбинацию двух физически различных величин и J. Поэтому вектор H вспомогательный вектор, удобный тем, что уравнение для него зависит только от внешних токов (токов проводимости)

- Дифференциальная форма теоремы о циркуляции вектора Н С помощью теоремы Стокса устанавливается интегральная форма теоремы

где I – есть алгебраическая сумма токов проводимости, охватываемых контуром интегрирования.

Поле в линейном однородном изотропном магнетике:

Магнитное поле B при наличии магнетиков определяется всеми токами, в том числе и токами намагничивания. В отличие от токов проводимости, токи намагничивания заранее неизвестны. Распределение токов намагничивания зависит от свойств и конфигурации магнетика, и конфигурации магнитного поля B. Поэтому находить токи намагничивания довольно сложно.

Исключение составляет случай, когда все пространство заполнено однородным изотропным (одинаковым по всем направлениям) магнетиком. Из областей, где B  0, магнетик можно удалить (или заполнить магнетиком, если там его не было), поскольку поле при этом нигде не изменится. Рассмотрим случай объемных токов проводимости. Предельным переходом к линейным и/или поверхностным токам полученный результат распространяется и на общий случай.

В магнетике, помещенном в магнитном поле возникают токи намагничивания

. Так как магнетик заполняет все пространство, то поверхностные токи намагничивания отсутствуют. Таким образом, конфигурация токов намагничивания и токов проводимости совпадают. Результирующий ток будет пропорционален току проводимости

. Следовательно, индукция результирующего поля B пропорционально индукции магнитного поля в отсутствии магнетика

. Можно утверждать, что магнитное поле при заполнении пространства однородным магнетиком возрастает в  раз.

Если разделить обе части равенства на , то получим

– в рассматриваемом случае поле H оказывается таким же, как и в вакууме.

Эти формулы справедливы и в тех случаях, когда однородный магнетик заполняет весь объем, ограниченный поверхностями, которые образованы линиями вектора (поля тока проводимости).

Граничные условия на границе раздела двух магнетиков:

Граничные условия для B и H. При переходе границы раздела двух магнетиков вектора B и H терпят разрыв, т.е. меняются скачком. Найдем связь между векторами по разные стороны границы (граничные условия). Эти условия, как и в случае диэлектрика, установим с помощью теоремы Гаусса и теоремы о циркуляции. Для векторов B и H эти теоремы имеют вид

, .

Возьмем замкнутую поверхность в виде прямого цилиндра, охватывающего некоторый участок границы раздела двух магнетиков. Считаем цилиндр достаточно тонким (чтобы на каждом основании поле менялось незначительно) и будем стягивать основания цилиндра к поверхности раздела. В пределе получим

или . Таким образом, нормальная составляющая вектора B оказывается одинаковой по обе стороны границы раздела.

Применим теорему о циркуляции вектора H для малого замкнутого контура, охватывающего некоторый участок границы. Будем стягивать контур к отрезку, лежащему на границе раздела. Если отрезок достаточно короткий (чтобы на отрезке с каждой стороны поле менялись незначительно), то в пределе получим

или .

Таким образом, если на границе раздела магнетиков токов проводимости нет (i  0), то тангенциальная составляющая вектора H одинакова по обе стороны границы раздела.

На границе раздела вектор B ведет себя аналогично вектору D, а вектор H – аналогично вектору E.

Эк. БИЛЕТ № 2

1. Поток вектора E. Теорема Гаусса для вектора E (в интегральной и дифференциальной формах).

2. Магнитный диполь. Магнитный момент диполя. Поле диполя. Сила и момент сил, действующие на магнитный диполь в магнитном поле.

1 Теорема Гаусса для вектора E (в интегральной форме) :

=> => ,

где – алгебраическая сумма зарядов, охватываемая этой поверхностью. Кружок на символе интеграла означает, что интегрирование проводится по замкнутой поверхности. Данная формула представляет собой теорему Гаусса.

(в дифференциальной форме):

=> => (дифф. форма),

2. Магнитный диполь – Система токов малых размеров (т.е. r >> a).

Магнитный момент:

Для плоского витка: , где S – площадь витка, n – положительная нормаль к поверхности

Сила, действующая на магнитный диполь:

Момент сил, действующие на магнитный диполь:

Эк. БИЛЕТ № 3

1. Теорема Гаусса для вектора E. Применение теоремы: поле равномерно заряженной плоскости, цилиндра, сферы.

О свойствах поля E. Определенное выше поле E обладает двумя чрезвычайно важными свойствами, которые позволяют решить ряд вопросов весьма просто и изящно. Одно из них это теорема Гаусса.

Теорема Гаусса. Зададимся некоторой элементарной площадкой dS. Определим вектор dS как вектор, по модулю равным dS и направленным вдоль ее нормали n. Заметим, что выбор направления вектора n (а следовательно и dS) условен, его можно направить и в противоположную сторону. В случае замкнутой поверхности принято нормаль n брать наружу области, охватываемой этой поверхностью. Поток dФ вектора E через площадку dS определяется как

. Если имеется некоторая протяженная поверхность S, то поток вектора E через нее

.

Поток вектора E через произвольную замкнутую поверхность S обладает замечательным свойством, которое выражается формулой

- Теорема Гаусса для вектора Е (интегральная форма)

- Теорема Гаусса для вектора Е (дифференциальная форма)

где – алгебраическая сумма зарядов, охватываемая этой поверхностью. Кружок на символе интеграла означает, что интегрирование проводится по замкнутой поверхности.

Написание многих формул и действия с ними значительно упрощается, если ввести векторный дифференциальный оператор . В декартовых координатах он имеет вид

, где x, y, z – орты осей X, Y, Z. Сам по себе векторный оператор  смысла не имеет. Он приобретает смысл только в сочетании со скалярной или векторной функцией, на которую символически умножается. Так, например, если вектор  умножить скалярно на вектор E, то получим

.

Таким образом, дивергенция вектора E может быть записана как или . Мы будем пользоваться вторым, более удобным обозначением. Тогда, например теорема Гаусса будет иметь вид

.