
Король А. В. / Практики Король А. В. / (2) Законы Ньютона. Работа. Энергия
.pdf
1Задачи по теме "Законы Ньютона. Работа. Энергия."
Пожелание/совет: освежите в памяти основные кинематические понятия, соотношения, формулы. Для этого можно воспользоваться материалом лекциий 2,3 или/и §§ 5-10, 11-13 учебника "Курс Физики"(автор Т. И. Трофимова).
Внимание: ниже в тексте векторы обозначаются жирными буквами!
1.1Задача 1.
Шкаф массой m = 50 кг, стоящий на горизонтальном полу, пытаются сдвинуть с места прикладывая горизонтальную силу F = 150 Н. Коэффициент трения шкафа о пол = 0:4. Чему равна сила трения?
N |
M |
F |
FT |
MG |
1)Неправильное решение.
Сила трения Fт зависит он реакции опоры N и коэффициента трения : Fт = N. Поскольку шкаф не двигается по вертикали, значит силы тяжести и реакции опоры уравновешивают друг друга: N = mg.
Следовательно, Fт = mg 0:4 50 10 = 200 Н.
Очевидно, что такое решение приводит к явлению, противоречащему опыту и здравому смыслу:
человек толкает шкаф влево (см. рис.) с силой F = 150 H, сила трения направлена вправо и превосходит 150 H. Иными словами, по 2-му закону Ньютона шкаф должен начать двигаться влево, на толкающего человека.
2)Правильное решение. Выражение Fт = N справедливо в случае трения скольжения,
когда тело двигается относительно поверхности. Оно же определяет максимально возможное значение трения покоя. Если приложенная к телу горизонтальная сила F по модулю меньше N, то тело покоится. При этом сила F компенсируется силой трения покоя Fт.
Именно эта ситуация реализуется в данной задаче. Чтобы сдвинуть шкаф с места необходимо приложить горизонтальное усилие > 200 Н. Поскольку F = 150 Н, то шкаф покоится и сила трения покоя также равна 150 Н.
Правильный ответ: Fт = 150 Н.
1

1.2Задача 2.
Под каким углом нужно тянуть санки по горизонтальной поверхности, чтобы они двигались с постоянной скоростью, а сила тяги была минимальной? Коэффициент трения равен .
Y |
N |
F |
|
α |
|
|
|
|
FT |
|
X |
|
MG |
|
Решение.
По условию, скорость санок постоянна: v = 0 =) ускорение отсутствует, a = 0. Из 2-го закона Ньютона следует, что векторная сумма всех сил, приложенных к санкам, тоже равна нулю:
F + mg + N + Fт = 0 : |
(1) |
||
Проецируя это равенство на оси X и Y , получаем: |
|
||
F sin + N mg = 0 |
|
||
{ F cos Fт = 0 |
(2) |
||
Санки двигаются, поэтому Fт является силой трения скольжения: Fт = N. Используя это |
|||
соотношение в (2), находим зависимость величины силы тяги F от угла : |
|
||
|
mg |
(3) |
|
F = |
|
: |
|
cos + sin |
|||
F достигает минимального значения, когда знаменатель в (3) максимален. Вычисляя производную суммы (cos + sin ) по и приравнивая результат к нулю, находим искомый угол:
tg = |
=) |
= arctg : |
(4) |
||
Подставляя |
(4) в (3), находим минимальное значение силы |
|
|||
Fmin = |
|
mg |
: |
(5) |
|
|
|
||||
√ |
|
||||
1 + 2 |
|||||
1.3Задача 3.
Парашютист массой m = 100 кг делает затяжной прыжок (т.е., не раскрывая парашют) с начальной скоростью v0 = 0. Найти зависимость скорости парашютиста он времени, если сила сопротивления воздуха Fс = kv, где k = 20 кг/с.
Решение.
Под действием силы тяжести mg парашютист начинает двигаться вниз (это направление выберем за направление оси X). По мере того, как скорость парашютиста возрастает, возрастает и сила сопротивления, направленная против скорости, т.е. вверх, поскольку Fс "" v.
Скорость будет возрастать то тех пор, пока Fс не сравняется по величине с mg. Начиная с этого момента, парашютист будет падать с постоянной скоростью
vmax = |
mg |
50 м/c = 180 км/чаc: |
(6) |
k |
2

Для нахождения зависимости v = v(t) воспользуемся 2-м законом Ньютона. Учитывая, что ускорение = производная скорости по времени, пишем
mg + Fс = ma |
=) mg kv = m |
dv |
(7) |
||
dt |
|
||||
Проецируем уравнение (7) на вертикальную ось (направлена вниз): |
|
||||
mg kv = m |
dv |
: |
|
|
(8) |
dt |
|
|
|||
|
|
|
|
|
|
Полученное уравнение является дифференциальным, т.е. оно связывает неизвестную функцию v(t) и её производную. Решить дифференциальное уравнение означает найти функцию ему удовлетворяющую.
Решаем уравнение методом разделения переменных: собираем все множители, относящиеся к v в одной части уравнения, а то, что относится ко времени t - в другой части.
k |
v m |
) |
[ ( |
k |
)] |
( |
|
m ) |
|
|||||||||
dv |
|
|
k |
|
|
|
mg |
|
|
|
|
|
k |
|
(9) |
|||
mg |
|
= |
dt |
= |
d ln |
|
|
v |
} |
= d |
|
|
t |
: |
||||
|
|
|
|
|
| |
|
|
{z |
|
|
=h |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
{z |
|
} |
|
|
=f
Математическое дополнение.
Если дифференциалы двух функций f = f(t) и h = h(t) переменной t совпадают, т.е. df = dh, то сами функции отличаются на произвольную постоянную (т.н., постоянная интегрирования): f = h + C.
Воспользовавшись Математическим дополнением, пишем |
|
|||||
ln ( |
mg |
v) |
|
k |
(10) |
|
|
= |
|
t + C : |
|||
k |
m |
|||||
где C - постоянная. Для её нахождения, учтём, что по условию, в начальный момент времени скорость v0 = v(t = 0) = 0. Рассматривая соотношение (10) в момент времени t = 0, находим постоянную интегрирования
|
mg |
|
|
|
|
|
C = ln ( k ) = ln (vmax) ; см. ф. (6): |
|
|
|
|||
Вспоминая свойство логарифма, ln a ln b = ln(a=b), получаем: |
|
|||||
ln (1 |
v |
k |
|
(1 |
k |
|
vmax ) = |
mt =) |
v(t) = vmax |
e m t) |
(11) |
||
Последнее равенство есть решение задачи.
Прежде чем проанализировать зависимость v(t), найдем закон изменения со временем координаты x парашютиста. Полагая начало координат в точке, где парашютист находился в t = 0, получаем
x(t) = ∫0 |
t |
m |
|
k |
m |
|
||
|
|
|
||||||
v(t)dt = vmax (t + |
|
e |
m |
t |
|
) |
(12) |
|
k |
k |
|||||||
3
Анализ найденных решений
|
( |
) |
|
|
|
|
|
||||
v(t) = vmax |
1 |
e |
t |
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
||||||
|
(t + e |
t |
|
) |
где = |
|
и vmax = g : |
(13) |
|||
x(t) = vmax |
|
k |
|||||||||
|
|
|
|||||||||
Интервал времени характеризует время, в течение которого сила сопротивления "проявляет"себя. Из условия следует = 5 с.
Действительно, при малых временах, t , используя известное разложение exp( t= )
1t= + t2=2 2, получаем
v(t) vmaxt= = gt |
2 |
|
|
gt2 |
(14) |
|
x(t) vmax [t + (1 |
t= + |
t |
) |
] = |
|
|
2 2 |
2 |
|
||||
Эти формулы характеризуют зависимости v(t) и x(t) при свободном падении под действием только mg. Это есть следствие того, что в пределе t сила сопротивления пренебрежимо мала по
сравнению силой тяжести: Fс mg. |
t= ) ! 0, получаем |
В противоположном пределе больших времен, t , полагая exp( |
|
v(t) vmax |
(15) |
x(t) vmax(t ) vmaxt |
|
т.е. зависимости, характеризующие движение с постоянной скоростью. Как отмечалось выше, это происходит, когда сила сопротивления компенсирует силу тяжести, Fс = mg.
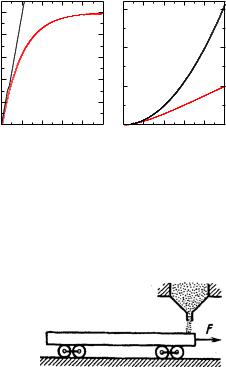
Левая панель рисунка иллюстрирует зависимость v(t)=vmax, правая панель - x = x(t) (в километрах). Жирные (красные) линии соответствуют точным решениям (13) , пунктирные (чёрные) - зависимостям в отсутствие силы сопротивления, ф. (14). При t оба типа зависимостей совпадают.
V(T)/V MAX
1
0.8
0.6
0.4
0.2
0
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
KM |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X(T), |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
τ |
2τ |
3τ |
4τ |
5τ |
0 |
τ |
2τ |
3τ |
4τ |
5τ |
Вопрос для самостоятельного обдумывания: как Вам кажется, что изменится в решении/формулах/численных значениях, если парашютист начинает движение с раскрывшимся парашютом? Подсказка: коэффициент k в Fс = kv пропорционален поперечному размеру ("радиусу") падающего объекта: k / R.
1.4Задача 4.
Платформа массы начинает двигаться под действием постоянной силы . Из неподвижного бункера на неё высыпается песок со скоростью погрузки k (кг/с). Найти зависимость от времени скорости и ускорения платформы при погрузке.
Решение.
Масса тела (платформа + песок) не является постоянной, поэтому пользоваться законом Ньютона, записанным в виде F = ma, нельзя.
4
Воспользуемся более общей формулировкой закона:
dp = Fdt : |
(16) |
Здесь dp - изменение импульса тела за бесконечно-малый интервал времени dt.
Найдем выражение для dp. Пусть в момент времени t масса платформы с находящимся на ней песком равна m, а её скорость есть v. Через dt масса изменилсь и стала равной m + dm (dm - масса добавленного песка), а скорость стала v + dv. Изменение (=приращение) импульса платформы вычисляется следующим образом:
dp = (m + dm) (v + dv) mv = mdv + vdm : |
(17) |
В правой части равенства пренебрегли слагаемым dm dv, которое является более высокого порядка малости по сравнению с двумя написанными.
Используя (17) в (16) записываем 2-й закон Ньютона:
mdv + vdm = Fdt : |
(18) |
Движение тележки – одномерное, по горизонтали. Выбирая ось X вдоль направления силы F и проецируя уравнение (18) на ось X, получаем скалярное дифференциальное уравнение:
mdv + vdm = F dt : |
(19) |
Учтем, что песок загружается с постоянной скоростью погрузки, k. Это означает, что от момента начала погрузки (t = 0) до момента t масса загруженного песка равна kt. Поэтому, масса системы "платформа + песок"в этот момент времени есть m = m0 + kt. Приращение массы dm за dt определяется dm = kdt. Используя эти соотношения в (19), пишем
(m0 + kt)dv + vkdt = F dt |
|
=) |
(m0 + kt)dv = (F |
|
kv)dt |
=) |
dv |
= |
dt |
(20) |
||||||||
|
|
F kv |
m0 + kt |
|||||||||||||||
В последнем уравнении в (20): |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
dv |
|
ln(F |
|
kv) |
|
dt |
|
|
ln(m |
+ kt) |
|
|
|
|
|||
|
= d ( |
|
|
|
) ; |
|
|
= d |
( |
|
0 |
|
) |
|
|
|
(21) |
|
|
F kv |
|
k |
|
|
m0 + kt |
|
k |
|
|
|
|
||||||
Вспоминая математическое дополнение, сформулированное в предыдущей задаче, получаем:
ln(F |
kv) |
= |
ln(m0 kt) |
+ C : |
(22) |
k |
|
k |
|||
|
|
|
|
где C - постоянная. Для нахождения постоянной интегрирования C учтём, что в начальный момент времени скорость v0 = v(t = 0) = 0 ("платформа начинает двигаться"). Рассматривая соотношение (22) в момент времени t = 0, находим
C = |
ln(F ) |
|
ln(m0) |
: |
|
|
|
(23) |
|||||
|
k |
|
|
|
|
||||||||
|
|
|
k |
|
|
|
|
||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln(F |
kv) + ln(F ) = ln(m0 kt) ln(m0) =) ln |
F |
= ln |
m0 kt |
|
||||||
|
|
F kv |
m0 |
||||||||||
=) |
|
F |
|
= |
|
m0 kt |
|
|
|
(24) |
|||
|
F kv |
|
m0 |
|
|
||||||||
5

Из (24) находим зависимость v(t):
F t v(t) = m0 + kt
Дифференцируя, находим ускорение
a(t) = |
dv |
= |
F m0 |
|
dt |
(m0 + kt)2 |
|||
|
|
Полагая в (25) и (26) k = 0 (песок не загружается, масса платформы остаётся равной m0)
v(t) = |
F t |
= at; |
a = |
F |
- платформа движется с постоянным ускорением, к. и д.б. |
|
m0 |
||||
|
m0 |
|
|
||
(25)
(26)
1.5 Задача 5. |
|
|
|
|
Тело начинает скользить с наклонной плоскости высотой |
|
|
|
|
h и углом наклона к горизонту и движется далее по гори- |
|
|
|
|
зонтальному участку. Коэффициент трения на всем пути |
H |
|
|
|
|
α |
|||
постоянен и равен . Определите расстояние s, пройденное |
|
|||
|
|
|
|
|
телом на горизонтальном участке, до полной остановки. |
|
|
S |
|
|
|
|
|
|
Решение.
На тело действует сила трения, которая его тормозит. Результатом совершения работы силой трения является выделившееся тепло Q = Aтр.
В присутствии силы трения закон сохранения энергии выглядит следующим образом:
E1 = E2 + Q; |
(27) |
где E1 и E2 - начальная и конечная полная механическая энергия (= сумме кинетической Eк и потенциальной Eп).
По условию, в начале и конце движения тело покоится, т.е. Eк1 = Eк2 = 0. Отсчитывая потенциальную энергию силы тяжести от горизонтального уровня, получаем: Eп1 = mgh, Eп2 = 0. Следовательно:
E1 = mgh; E2 = 0: |
(28) |
Вычислим работу силы трения (скольжения), которая совершается на наклонном и на горизонтальном участках: Aтр = A(трн) + A(трг).
На наклонном участке, длина которого l = h= sin , сила трения равна Fтр(н) |
= mg cos . На |
|||||||||
горизонтальном участке Fтр(г) = mg. |
|
|
|
|
|
|
||||
Следовательно: |
|
|
|
|
|
|
|
|
|
|
Aтр(н) = |
Fтр(н)l = |
mgh ctg |
= |
Aтр |
= |
mg |
hctg + s : |
(29) |
||
{ Aтр(г) = |
Fтр(г)s = |
|
|
|||||||
mgs |
|
) |
|
|
|
( |
) |
|
||
Используя равенства (28) и (29) в (27), получаем: |
|
|
||||||||
h = (hctg + s) |
=) |
Ответ: s = |
|
h |
(1 ctg ): |
(30) |
||||
|
|
|||||||||
|
|
|||||||||
6

1.6Задача 6.
Гиря массой m = 10 кг падает с высоты h = 0:5 м на подставку, скрепленную с пружиной жесткостью k = 40 Н/см. Определите деформацию x пружины. Выделением тепла и массой подставки пренебречь.
Решение.
В отсутствие сил трения закон сохранения энергии выглядит следующим образом:
Eп1 + Eк1 = Eп2 + Eк2; |
(31) |
где индексы 1 и 2 характеризуют начальное и конечное положение системы "гиря+пружина"; Eк обозначает кинетическую энергию, Eп - потенциальную.
В начальном и конечном положении гиря не движется, т.е. Eк1 = Eк2 = 0.
Потенциальная энергия в начальном положении определяется силой тяжести. Отсчитывая высоту от подставки ("нулевой уровень"), находим: Eп1 = mgh.
В конечном положении:
(а) тело опустилось вниз на величину x от нулевого уровня. Соответствующая потенциальная
энергия равна |
mgx. |
|
||||||
(б) пружина сжалась на величину x, запася энергию kx2=2. |
|
|||||||
Потому, Eп2 = |
mgx + kx2=2. |
|
||||||
Используя полученное в ур-ии (31), находим |
|
|||||||
Eп1 = Eп2 |
=) x2 2bx 2bh = 0 |
(32) |
||||||
где для краткости обозначено b = mg=k. |
|
|||||||
Разрешая квадратное уравнение, оставляем положительный корень (почему?): |
|
|||||||
x = b + √ |
|
= b (1 + √ |
|
|
|
) : |
|
|
|
1 + |
4h |
|
(33) |
||||
b2 + 4bh |
||||||||
b |
||||||||
При подстановке численных значений, учтем, что k = 40 Н/см = 4 103 Н/м =) b = 1=40 м.
Ответ: x = 10=40 = 0:25 м.
1.7Задача 7.
С вершины идеально гладкой сферы радиусом R = 1:2 м соскальзывает небольшое тело. Определите высоту h (измеренную от вершины сферы), с которой тело отрывается от сферы.
Решение.
Поскольку трения нет (гладкая сфера!), то при движении тела сохраняется полная механическая энергия: Eп + Eк = const. Применяя это равенство к положениям A и B тела (см. рис.),
7

записываем (отсчитывая потенциальную энергию от центра сферы): |
|
||
mgR = mg(R h) + |
mv2 |
=) 2gh = v2 : |
(34) |
2 |
|||
В уравнении (34) два неизвестных: скорость v в момент отрыва и высота h. Для нахождения h необходимо установить ещё одну её связь с v.
Помогут следующие рассуждения.
До отрыва тело двигается по дуге окружности AB под действием двух сил: тяжести mg и реакции опоры N.
После отрыва тело движется только под действием mg, по параболе (пунктирная линия).
Момент отрыва характеризуется тем, что тело еще находится на сфере, но реакция опоры исчезает: N = 0.
Применяя 2-й закон Ньютона, получаем, что в момент отрыва ma = mg, значит a = g. При любом движении ускорение a содержит тангенциальную a и нормальную an составляющие: a = a + an. На дуге AB (включая точку отрыва B) нормальное ускорение направлено у центру сферы. В самой точке B: an = g cos . Нормальное ускорение связано со скоростью v и кривизной 1=R траектории: an = v2=R. Из двух написанных соотношений получаем
|
v2 |
|
|
g cos = |
|
; где cos = (R h)=R (см. рис.). |
(35) |
|
|||
|
R |
|
|
Это и есть второе уравнение, связывающее v и h.
Разрешая систему уравнений (34) и (35) относительно h находим ответ: h = R=3.
1.8Задача 8.
Локомотив массы m начинает двигаться так, что величина его скорости меняется по закону p
v = s, где > 0 некоторая постоянная, а s - пройденный путь. Найти работу равнодействующих всех сил, приложенных к локомотиву, за первые t секунд его движения.
Решение.
Искомая работа A равна изменению кинетической энергии локомотива:
A = Eк(t) Eк(0): |
(36) |
Здесь Eк(t) = mv2=2 кинетическая энергия в момент t, а Eк(0) = mv02=2 - в момент t = 0. По
условию, v0 = 0 =) Eк(0) = 0.
p
Для определения зависимости v(t), воспользуемся условием, v = s, и определением v = ds=dt. Тогда
|
ds |
|
p |
|
|
ds |
|
p |
|
|
||
|
|
|
= s |
=) p |
|
= dt =) |
2 s = t: |
|||||
|
dt |
|||||||||||
|
s |
|||||||||||
Из последнего равенства и из условия следует v = 2t=2. |
||||||||||||
Ответ: |
|
|
|
|
|
|
||||||
A = |
m 4t2 |
|
|
|
(37) |
|||||||
|
|
|
|
|||||||||
|
|
|
8 |
|
|
|
|
|
|
|
|
|
8
1.9Задача 9.
Материальная точка (=частица) движется в плоскости (xy). Её потенциальная энергия зависит от координат x и y по закону Eп = xy, где = 6 Дж/м2 - постоянная. Найти силу
F, действующую на частицу в точке (2; |
3) м. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Сила F связана с потенциальной энергией соотношением: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
F = |
|
|
@Eп |
i |
@Eп |
|
j |
@Eп |
k : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(38) |
||||||
|
|
@x |
@y |
@z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, частные производные Eп по декартовым координатам определяют компоненты |
||||||||||||||||||||||||||||||
силы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Применяя (38) к данным задачи, находим: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
8 |
|
|
|
|
|
@E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fx = |
|
п |
= y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
@x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
> |
|
|
|
|
|
@Eп |
|
|
|
|
|
|
|
|
|
F = yi + xj |
|
|
|
|
|
|
|
|
||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
||
> |
F |
y |
= |
|
|
|
= x |
|
|
= |
|
8 |
|
|
|
|
|
|
|
|
|
(39) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
@y |
|
|
|
|
|
) |
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
2 |
|
|
2 2 |
|
|
||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|||||||||
< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
F = √Fx + Fy + Fz = x + y |
|
||||||||||||
> |
|
|
|
|
|
@Eп |
|
|
|
|
|
|
|
|
> |
|
||||||||||||||
Fz |
= |
|
|
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|||||
> |
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
> |
|
|
|
|
|
@z |
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для искомой точки, получаем ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
F |
= |
|
|
18i + 12j ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
8 |
|
|
|
|
F |
= |
|
p324 + 144 = p468 = p484 |
|
16 = 22√1 |
22 |
(1 |
) 21:6 |
Н : |
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
484 |
|
484 |
||||||||||||||||||||||||||
1.10Задача 10.
Принимая, что атмосфера на Луне отсутствует, определите скорость падения метеорита на ее поверхность. Скорость метеорита вдали от Луны считать малой. Учесть, что масса Луны MЛ в 81 раз меньше массы Земли ,MЗ а её радиус RЛ в 3:7 раза меньше земного. Радиус Земли равен 6400 км.
Решение.
Скорость, которую надо вычислить, представляет собой вторую космическую скорость для Луны. Эта та минимальная скорость, с которой нужно запустить тело с поверхности Луны, чтобы оно, преодолев притяжение Луны, удалилась на бесконечно-большое расстояние. Процесс, указанный в условии, является обратным описанному выше.
В отсутствие атмосферы метеорит падает без трения под действием силы гравитационного притяжения к Луне, F = GmMЛ=r2, где m - масса метеорита, r - расстояние между ними. Потенциальная энергия гравитационного взаимодействия определяется соотношением
Eп = G |
mMЛ |
: |
(40) |
|
r |
||||
|
|
|
9

При движении метеорита его полная механическая энергия сохраняется: Eк + Eп = const. В начале движения v0 = 0 и r0 = 1 ("вдали" от Луны), так что Eк = Eп = 0 и const = 0. Следовательно, на любом расстоянии r выполняется равентсво
mv2 |
mMЛ |
|
||
|
G |
|
= 0: |
|
2 |
r |
|||
|
|
|||
Скорость метеорита vп в момент падения на Луну находим, подставляя r = RЛ в (41):
√
vп = 2GMЛ : RЛ
(41)
(42)
Из условия задачи известно, что RЛ=RЗ = 1=3:7 и MЛ=MЗ = 1=81. Радиус Земли RЗ = 6400 км известен, а её масса MЗ - нет. Решить задачу надо не прибегая к справочнику или Google.
Применим следующие рассуждения. Вблизи поверхности Земли, на любое тело действует сила тяжести mgЗ, где gЗ - ускорение свободного падения на Земле. Сила тяжести, определенная из закона всемирного тяготения, записывается как GmMЗ=RЗ2 . Следовательно, ускорение свободного падения выражается через массу и радиус Земли
gЗ = G |
MЗ |
: |
(43) |
|
RЗ2 |
||||
|
|
|
Такое же равество может быть записано для любой планеты/звезды. В частности, для Луны
gЛ = G |
MЛ |
: |
(44) |
|
RЛ2 |
||||
|
|
|
Зная gЗ, и воспользовавшись данными в условии, найдем ускорение свободного падения на Луне.
Деля почленно уравнение (44) |
на (43), получаем |
|
||||||
|
MЛ |
|
RЗ |
2 |
gЗ |
|
|
|
|
|
|
|
|
||||
gЛ = gЗ |
|
( |
|
) |
|
|
; |
(45) |
MЗ |
RЛ |
6 |
||||||
т.е., ускорение свободного падения на Луне примерно в 6 раз меньше земного.
Используя (45) в (42), находим p
vп p2gЗRЗ 0:2vII : (46)
6 3:7
Здесь vII обозначает вторую космическую скорость для Земли:
vII = √ |
|
11:2 км/с : |
|
|
(47) |
2gЗRЗ |
2 |
, RЗ = 6400 |
|||
Этот результат получен для gЗ = 9:8 м/с |
км. |
||||
Таким образом, ответ: |
|
|
|
||
vп 0:2 11:2 2:2 км/с : |
|
|
(48) |
||
10
