10797

задаётся уравнение второго порядка, относящееся к виду (2.4), с конкретными числовыми коэффициентами. В нём могут присутствовать взаимное произведение координат x и y ( B ¹ 0 ) или переменные x и y без

квадратов ( D ¹ 0 или E ¹ 0 ). Это будет означать, что в исходной системе координат уравнение не является каноническим. Нужно найти другую систему координат, в которой уравнение приобретёт канонический вид. Это даст возможность легко построить график заданной кривой.

Для этих целей используются только те преобразования системы координат, которые не изменяют расстояния между точками, то есть не деформируют кривую. К таким преобразованиям, в частности, относятся параллельный перенос и поворот осей координат. Этих преобразований достаточно для

приведения уравнения линии второго порядка к

каноническому виду.

Я снова обратился к аналитической геометрии и стал изучать, что происходит с уравнениями при том или ином преобразовании координат.

40

2.7. Кроме исходной прямоугольной декартовой системы координат xO y рассмотрим другую, начало

которой разместим в точке Oў(x0 ; y0 ). Оси Oўxў и

Oўyўрасположим параллельно соответствующим осям O x , O y и одинаково с ними направим. Масштаб сохраняем. Такой переход от системы xO y к системе xўOўyў называется параллельным переносом осей

координат.

Для произвольной точки M координаты относительно исходных осей обозначим через (x; y), а координаты по отношению к «новым» осям обозначим (xў; yў). Поскольку имеет место векторное равенство

OM = OOў+ OўM (рис. 2.17), то можно записать в координатах

41

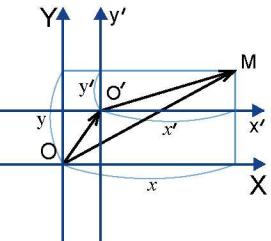
Рис. 2.17

Например, если совершается параллельный перенос осей координат к новому началу Oў(1; 2), то

преобразовании системы координат уравнение прямой y = 3x - 1 изменится. Используя (2.5)

Видим, что после параллельного переноса уравнение может упроститься (а может и усложниться). Важно правильно выбирать новое начало координат.

параллельный перенос

мп xў= x - 1

п

н . ппоyў= y + 3

По новому уравнению xў2 + yў2 = 4 легко определить окружность радиуса 2 с центром в начале координат Oў(1;- 3). На рисунке 2.18 отражено построение, соответствующее такому преобразованию.

параллельного переноса, задаваемого формулами

рисунком 2.19.

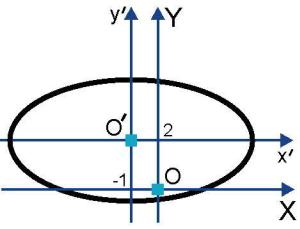. Рис. 2.19

44

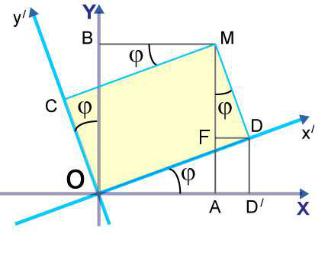
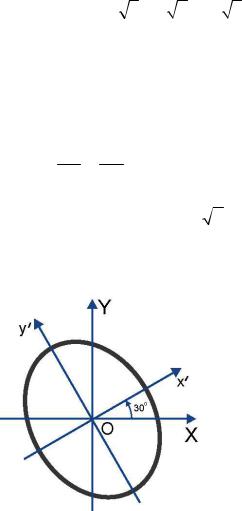
2.8. Можно выполнить поворот исходной системы координат xO y вокруг начала координат на

угол j (положительным считается поворот против часовой стрелки) в положение xўOyў (рис. 2.20).

Пусть точка M имеет в исходной системе координаты (x; y) и координаты (xў; yў) в «новой»

системе координат xўOyў. Чтобы установить связь

между исходными и новыми координатами точки M , выполним дополнительные построения. Через A и B обозначим проекции точки M на координатные оси

O x и O y , а через D и C — проекции её на оси O xў и O yў (рис. 2.20). Из точки D опустим перпендикуляры на отрезок AM (основание перпендикуляра — точка F ) и ось O x (основание перпендикуляра – точка Dў).

Рис. 2.20

45

Тогда из геометрических соображений получаем, что

x = OA = ODў- ADў= ODў- FD =

= OD cosj - MD sin j = xўcosj - yўsin j ,

y = AM = AF + FM = DDў+ MF =

= OD sin j + MD cosj = xўsin j + yўcosj .

Таким образом, формулы, выражающие исходные координаты (x; y) произвольной точки M через её новые координаты при повороте осей на угол j , имеют вид

равенствах (2.7) поменять местами исходные и новые

46

перегруппируем слагаемые

xў2 (21+ 6 + 5)+ xўyў(- 143 + 43 + 103)+

+ yў2 (7 - 6 + 15)= 64

и придём к уравнению

32xў2 + 16 yў2 = 64

или

xў2 + yў2 = 1. 2 4

Это уравнение эллипса с полуосями a = 2 и b = 2 . Заметим, что для него a < b , а фокусы расположены на оси Oyў(рис. 2.21).

Рис. 2.21

48

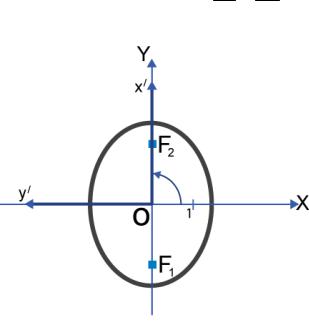
пришли в предыдущем примере, поменять местами оси координат, то сохранится условие a > b , использовавшееся при выводе канонического уравнения эллипса. Для этого можно выполнить поворот на угол

sinϕ = 1:

мпx = - yў

п

н

ппо y = xў

и получим в новой системе уравнение xў2 + yў2 = 1.

4 2

Рис. 2.22

49