
10623
.pdf
- 30 -
Теорема 3.3. ( Об эквивалентности пар в пространстве ). Две пары,
лежащие в параллельных плоскостях и имеющие равные по величине и по знаку моменты, эквивалентны.
Для доказательства этой теоремы нам понадобится следующая
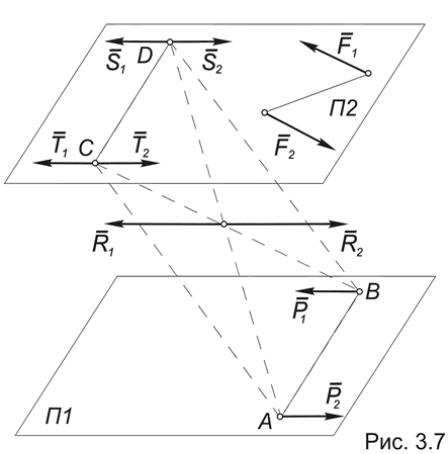
Лемма. Равнодействующая двух параллельных и равных по модулю сил равна их сумме, а ее линия действия проходит посредине между точками их приложения (Рис.3.6).
Для доказательства леммы достаточно к системе двух сил (P1, P2), приложенных соответственно в точках A и B, о которых идет речь в теореме, добавить уравновешенную систему сил (T1,T2), а затем воспользоваться аксиомой параллелограмма:
(P1, P2) ((P1, P2), (T1,T2)) ((P1,T1), (P2,T2)) (R1,R2) (R12 ),
где P1 = P2 = P, R12 = 2 P , а AС = BC .
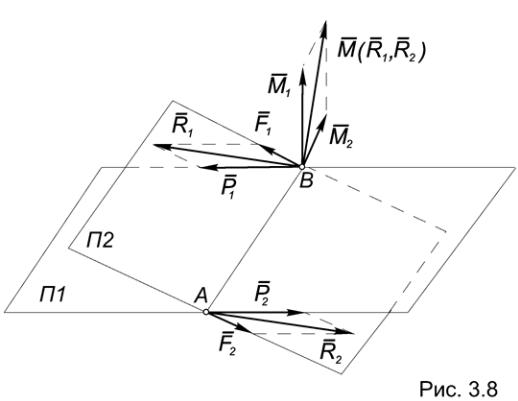
Переходя к доказательству теоремы, рассмотрим две пары сил (P1, P2) и (F1, F2), имеющие равные моменты и лежащие в параллельных плоскостях П1 и П2 соответственно (Рис.3.7).
Построим в плоскости П2 отрезок CD, равный и параллельный отрезку АВ и приложим в точках C и D две системы уравновешенных сил: (S1, S2) 0 и (T1, T2) 0, выбрав силы S и T равными по модулю и параллельными силам P.
На основании аксиом 2, 3 и последней леммы:
(P1, P2) ((P1, P2), (S1, S2), (T1, T2)) ((P1, T1), (P2, S2), (S1, T2))
((R1, R2), (S1, T2)) (S1, T2),
- 31 -
поскольку R1 (P1, T1) и R2 (P2, S2) также образуют уравновешенную систему сил, которую можно исключить.
Таким образом, мы получили две пары сил: (S1, T2) и (F1, F2), которые лежат в одной плоскости и имеют равные по величине и по знаку моменты. В силу предыдущей теоремы 3.2 они будут эквивалентны, откуда следует, что
(P1, P2) (S1, T2) (F1, F2).
Теорема доказана.
Следствие. Действие пары сил на ТТ не изменится при ее перемещении в параллельную плоскость, расположенную в пределах этого тела.
ПРИМЕЧАНИЕ. В силу этого следствия вектор-момент пары сил в пределах этого тела можно считать свободным.
3.4. Сложение пар сил
Теорема 3.4. Две пары, лежащие в пересекающихся плоскостях, эквивалентны одной паре с вектор-моментом, равным геометрической сумме век- тор-моментов слагаемых пар.
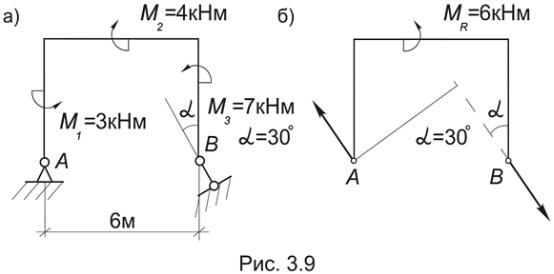
Для доказательства рассмотрим две пары сил (P1, P2) и (F1, F2), лежащие в плоскостях П1 и П2 соответственно, которые пересекаются по прямой АВ.
Не уменьшая общности можно считать, что плечи этих пар равны отрезку АВ этой прямой. Пусть М (P1, P2) = М1, а М (F1, F2) = М2 (Рис.3.8) .
- 32 -
Воспользовавшись аксиомой параллелограмма, получим:
((P1, P2), (F1, F2)) ((P1, F1), (P2, F2)) (R1, R2).
При этом момент результирующей пары с учетом теоремы Вариньона будет равен:
М (R1, R2) = МА (R1) = МА(P1) + МА(F1) = М (P1, P2) + М (F1, F2) = М1 + М2.
Теорема доказана.
Следствия:
1. Система n пар в пространстве эквивалентна одной паре с вектормоментом, равным геометрической сумме вектор-моментов слагаемых пар:
i=n
М= ∑ i (3.3)
i=1
2.Система n пар на плоскости эквивалентна одной паре с моментом,М
равным алгебраической сумме моментов слагаемых пар:
i=n |
|
М = ∑ М i |
(3.4) |
i=1 |
|
ПРИМЕЧАНИЕ. В соответствии с замечанием в конце предыдущего параграфа век- тор-момент пары сил в пределах рассматриваемого тела, как в математике, является свободным, поэтому последняя теорема может показаться излишней.
-33 -
Вдействительности между векторами в математике и векторами в ТМ продолжает оставаться различие, которое обнаруживается при рассмотрении системы аксиом, которым удовлетворяют векторы в математике и не удовлетворяют вектора сил.
3.5.Равновесие систем пар
Система пар сил, приложенных к ТТ, будет уравновешена, если момент результирующей пары равен нулю.
Таким образом, из соотношений (3.3) и (3.4) следуют условия равновесия
системы пар:
1. Необходимым и достаточным условием равновесия системы пар в пространстве является равенство нулю геометрической суммы вектормоментов слагаемых пар:
i=n
∑ М i = 0 . (3.5)
i=1
2. Необходимым и достаточным условием равновесия системы пар на плоскости является равенство нулю алгебраической суммы моментов слагаемых пар:
i=n
∑ М i = 0 . (3.6)
i=1
Условие (3.5) имеет геометрическую интерпретацию и означает замкнутость многоугольника, образованного из векторов моментов пар.
Пример 3.1. Определить опорные реакции рамы, загруженной системой пар (Рис.3.9).
- 34 -
Решение. Заменим систему пар, приложенных к раме, результирующей
парой по формуле (3.4): MR = M1 − M2 + M3 = 3 − 4 + 7 = 6 кНм.
Из условия равновесия систем пар (3.6) следует, что активную пару MR , приложенную к раме, может уравновесить только пара сил, образованных опорными реакциями, поэтому линия действия RA должна быть параллельной
RВ и
MR + M (RA, RВ) = 0,
откуда RA = RВ = MR /d , где d = 6cos30°= 3 |
|
м − плечо пары (RA, RВ). |
||||
3 |
||||||
Итак, RA = RВ = 6/( 3 |
|
) = (2 |
|
)/3 м. |
|
∙ |
3 |
3 |
|
||||
- 35 -
ГЛАВА 4. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
Одной из основных задач, решаемых статикой, является замена одной системы сил другой – эквивалентной ей.
Такая процедура позволяет все многообразие систем сил свести к простейшим каноническим системам, классифицировать их и получить уравнения равновесия, необходимые для решения практических задач.
Ключевую роль в проведении таких преобразований систем сил играет следующая теорема.
4.1. Лемма Пуансо
Мы уже выяснили, что силу, приложенную к ТТ, можно переносить вдоль линии ее действия. Сейчас мы увидим, что при определенных условиях эту силу можно переносить даже параллельно своему первоначальному положению.
Лемма Пуансо. Действие силы Р, приложенной к ТТ не изменится, если эту силу перенести в любую точку О этого тела – центр приведения, добавив пару сил с моментом, равным моменту силы Р относительно центра приведения.
Для доказательства рассмотрим силу Р, приложенную к телу в точке А
(Рис.4.1а).
Согласно аксиоме 3 действие силы Р на ТТ не изменится, если к ней добавить уравновешенную систему сил: (Р′, Р′′ ) 0.
- 36 -
Выберем силы этой уравновешенной системы так, чтобы они были равны по модулю и параллельны силе Р (Рис.4.1б) :
Р′ = Р = − Р′′ .
Тогда полученную систему трех сил можно трактовать как силу Р′ , приложенную в центре О, и пару сил (Р, Р′′ ) с моментом М (Р, Р′′ ) = МО (Р ):
Р (Р, (Р′, Р′′ )) (Р′ , (Р, Р′′ )) .
Лемма доказана.
Сила Р′, приложенная в точке О, называется приведенной, а пара (Р, Р′′ ) −
присоединенной.
Напомним, что пару (Р, Р′′ ) можно заменить моментом М , величина которого равна моменту силы Р относительно центра приведения О (Рис.4.1в), поэтому:
Р(Р′ , (Р, Р′′ )) (Р′, М ).
4.2.Теорема о приведении плоской системы сил
Теорема 4.1. Произвольную плоскую систему сил можно заменить одной силой R0 - главным вектором системы, приложенным в центре приведения и равным геометрической сумме всех сил системы, и главным моментом системы M0 , величина которого равна алгебраической сумме моментов всех сил системы относительно выбранного центра приведения.
Доказательство. Рассмотрим произвольную плоскую систему сил: (P1, P2,
…, Pn).
Воспользовавшись леммой Пуансо приведем каждую силу системы Pi к центру О, заменив ее приведенной силой Pi′ и присоединенной парой, эквивалентной моменту Mi , величина которого равна моменту силы Pi относительно выбранного центра приведения:
(P1, P2, …, Pn) ((P1′, P2′, …, Pn′), (M1, M2, ... , Mn)).
Приведенные силы, приложенные в центре приведения О, образуют систему сходящихся сил, которые согласно теореме 2.2 можно заменить равнодействующей R0 . При этом
i =n |
i =n |
(P1′, P2′, …, Pn′) R0 = ∑ |
Pi′ = ∑ Pi . |
i =1 |
i =1 |
Совокупность присоединенных моментов, эквивалентных присоединенным парам, в соответствии с теоремой 3.4 можно заменить моментом, величина которого равна алгебраической сумме присоединенных моментов:
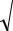
- 37 -
i =n |
i =n |
(M1, M2, ... , Mn) ~ M0 ; M0 = ∑ |
Mn = ∑ M0 (Pi ). |
i =1 |
i =1 |
Таким образом, первоначальная система сил будет эквивалентна:
i =n |
(P1, P2, …, Pn) ~ (R0 , M0), |
|
||
|
|
i =n |
|
|
где R0 = ∑ Pi |
- главный вектор системы, а M0 = ∑ M0 (Pi ) - главный мо- |
|||
i =1 |
|
|
i =1 |
|
мент системы относительно центра О. |
|
|||
Отметим, что модуль главного вектора плоской системы сил находится |
||||
по формуле (2.7): |
|
|
|
|
|
RO = |
|
, |
|
|
(∑ X i ) 2 + (∑Yi ) 2 |
( 4.1) |
||
где Xi , Yi - проекции силы Pi на оси координат.
ПРИМЕЧАНИЯ:
1.Для плоской системы сил под главным моментом системы часто также понимают величину этого момента.
2.Очевидно, что главный вектор R0 не зависит, а главный момент M0 зависит от выбора центра приведения.
4.3.Частные случаи приведения плоской системы сил
В зависимости от значений главного вектора R0 и главного момента M0 возможны следующие случаи приведения плоской системы сил.
1)R0 = 0, M0 = 0 - система сил находится в равновесии;
2)R0 = 0, M0 ¹0 - система эквивалентна паре сил с моментом, равным главному моменту системы, который в этом случае не зависит от выбора центра приведения;
3)R0 ¹ 0, M0 = 0 - система эквивалентна равнодействующей R, равной и эквивалентной главному вектору системы R0 , линия действия которой прохо-
дит через центр приведения: R = R0 , R ~ R0 ;
4) R0 ¹ 0, M0 ¹0 - система эквивалентна равнодействующей R, равной главному вектору системы R0 , ее линия действия проходит на расстоянии d = ½M0½/ R0 от центра приведения.
Чтобы убедиться в этом, достаточно рассмотреть доказательство леммы Пуансо в обратном направлении, сменив силу Р на R, а Р′ - на R0 .
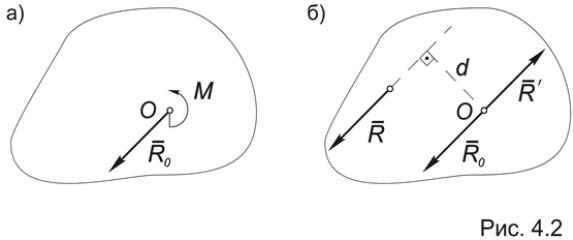
В самом деле, пусть система эквивалентна главному вектору R0 и главному моменту М0 (Рис.4.2а). Заменим М0 парой сил (R, R′ ) с моментом М(R, R′ ) = М0 , выбрав силы пары равными по модулю и параллельными R0 , а ее плечо d = ½M0½/ R0 (Рис.4.2б). Тогда
(R0 , М0) ~ (R0, (R, R′ )) ~ (R, (R0, R′ ) ~ R ,
- 38 -
поскольку (R0, R′ ) ~ 0. Таким образом, система (R0, М0) действительно эквивалентна равнодействующей R, линия действия которой проходит на расстоянии d = ½M0½/ R0 от центра приведения.
Следствием этого случая приведения является
Теорема Вариньона (о моменте равнодействующей плоской системы сил)
Момент равнодействующей плоской системы сил относительно произвольного центра О равен алгебраической сумме моментов всех сил системы относительно этого центра.
Выбирая центр О, о котором идет речь в теореме, в качестве нового центра приведения системы сил, состоящей из единственной силы - равнодействующей R, и учитывая, что R = R0 получим:
M0 (R) = ± R× d = ± R×½M0½/ R0 = M0 = S M0 (Pi )
4.4. Уравновешенная система сил
Необходимым и достаточным условием равновесия плоской системы сил
является равенство нулю главного вектора и главного момента системы:
R0 = 0, M0 = 0. |
(4.2) |
Из этого условия следуют уравнения равновесия плоской системы сил, |
|
которые можно записать в трех различных формах: |
|
1) Первая форма: |
|
S MA = 0; |
|
S X = 0; |
(4.3) |
S Y = 0.
2) Вторая форма:
|
- 39 - |
S MA = 0; |
|
S MB = 0; |
(4.4) |
SY = 0, где ось Oy неперпендикулярна отрезку АВ.
3)Третья форма:
SMA = 0;
S MB = 0; |
(4.5) |
S MС = 0, где точки А, В и С не лежат на одной прямой.
Таким образом, уравнения (4.3), (4.4) или (4.5) эквивалентны условиям (4.2) и наоборот.
В самом деле, условие R0 = 0 означает, что ½R0½= R0 = 0. Поэтому с учетом (4.1) : R02 = (S X)2 + (S Y)2 = 0, откуда и следуют два последних уравнения
(4.2).
Первое из уравнений (4.3) получается из условия равенства нулю главного момента, если в качестве центра приведения взять точку А.
Докажем теперь, что уравнения (4.4) эквивалентны условиям равновесия системы (4.2).
Первое из уравнений (4.4) будет выполняться в двух случаях:
1)система сил, приложенных к ТТ, уравновешена и ее равнодействующая равна нулю;
2)равнодействующая сил, приложенных к ТТ, отлична от нуля, при этом
еелиния действия проходит через точку А.
Пусть одновременно выполняются два первых уравнения системы (4.4). Это по-прежнему возможно в двух случаях:
1)равнодействующая R = 0;
2)равнодействующая R ¹ 0 и ее линия действия одновременно проходит через точки А и В.
Если в дополнение к этим двум уравнениям выполняется и третье урав-
нение (4.4), то это означает, что Ry = S Yi = 0.
При условии, что R неперпендикулярна этой оси – отсюда будет следовать, что R = 0, то есть система сил уравновешена.
Аналогично можно доказать, что условия (4.2) будут следовать из урав-
нений (4.3) или (4.5).
ПРИМЕЧАНИЯ:
1.В частном случае для плоской системы сходящихся или параллельных сил уравнения в системах (4.3), (4.4) или (4.5) будут линейно зависимы. Это означает, что определитель системы алгебраических уравнений для определения опорных реакций таких систем сил становится равным нулю.
Например, для системы сил параллельных оси Oy уравнения (4.3) станут линейно зависимыми вследствие того, что второе из уравнений этой системы обратится в тождество, которое выполняется как для уравновешенных, так и для неуравновешенных систем.
Такие уравнения исключают из системы, уменьшая тем самым общее число уравнений для плоской системы сходящихся или параллельных сил с трех до двух.
2.В соответствии с предыдущим замечанием уравнения равновесия системы сил, параллельных оси Oy, можно записать в двух формах:
