
10622
.pdf
- 181 -
Рис.2.9
Введем локальную систему отсчета с ортами τ--N и n--Q, и обозначим через j угол, который орт τ составляет с осью Ох. В отличие от принятого ранее правила (§ 2.2.1) положительным будем считать момент, соответствующий растянутым нижним волокнам арки, то есть так, как принято в сопромате. Это сделано для удобства сравнения изгибающего момента в арке с изгибающим моментом в соответствующей балке.
Из условия равновесия левой части арки получим:
ΣMC(AС) = 0; M(x) = [VА×x -SPi ( x - ai)] - H× f(x),
или иначе:
M(x) = M(х)Б - H×f(x), |
(2.2) |
где M(х)Б = [VА×x-SPi×(x - ai)] - балочный изгибающий момент в сечении x.
- 182 -
Последняя формула означает, что при одинаковой нагрузке изгибающие моменты в арке меньше изгибающих моментов в балке соответствующего пролета на величину H× f(x), что наглядно показано на рис. 2.9, д, е.
Это обстоятельство позволяет применять арки для перекрытия больших пролетов – порядка десятков метров. При этом отношение высоты сечения такой арки к длине перекрываемого пролета, как правило, не превышает 1/100. Ни фермы, ни балки не позволяют достичь такого результата.
Для определения поперечной силы в арке составим уравнение:
Σn(лев) = 0; Q(x) = (VА -SPi)×cosj - H×sinj,
или, иначе
Q(x) = Q Б (x)×cosj - H×sinj , |
(2.3) |
где QБ (x) = VА -SPi - поперечная сила в соответствующей балке.
Таким образом, при одинаковой нагрузке поперечная сила в арке меньше поперечной силы в балке соответствующего пролета.
Чтобы определить продольную силу составим уравнение:
Σt(лев) = 0; N(x) = - [(VА -SPi)× sinj + H×cosj].
Найденную продольную силу также можно представить в виде:
N(x) = - [QБ (x)×sinj + H×cosj]. |
(2.4) |
Последняя формула показывает, что уменьшение изгибающего момента и поперечной силы в арке по сравнению с соответствующей балкой достигается за счет появления продольной силы, которая, как следует из (2.1), будет особенно значительной для арок с небольшим отношением fC /l.
Таким образом, в арке, как и в раме, в общем случае появляются все три составляющих внутренних усилий: M, Q и N .
2.4.3. Рациональная ось арки
Формула (2.2) показывает, что при заданной нагрузке изгибающие моменты в арке можно уменьшить вплоть до нуля, если соответствующим образом подобрать очертание ее оси.
Определение. Рациональной называется такая арка, изгибающие моменты в которой равны нулю.
Пусть арка с пролетом l и стрелой подъема fC загружена равномерно распределенной нагрузкой интенсивностью q(x).
- 183 -
Определим очертание рациональной оси такой арки, воспользовавшись соотношением (2.2). Полагая в нем M(x) = 0 , получим:
M(х)Б - H×f(x) = 0,
откуда найдем искомое уравнение:
y = f(x) = M(х)Б/ H.
Подставляя сюда выражение изгибающего момента в простой двухопорной балке, загруженной равномерно распределенной нагрузкой:
M(х)Б = (ql/2)×x - qx2/2,
и учитывая, что в силу (2.1) H = МСБ/fС = (ql2)/(8fС), получим уравнение рацио-
нальной оси арки, загруженной равномерно распределенной нагрузкой:
y = f(x) = (4fС/l2)×(xl - x2).
Как видим, такая арка имеет параболическое очертание.
Примечания
1.Глобальная система координат Оху, в которой мы рассматриваем арку, не совпадает
слокальной системой координат, введенной в § 1.3, поэтому приведенные там основные уравнения строительной механики, включая дифференциальные зависимости Журавского (1.10), в нашем случае выполняться не будут. В частности, у рассмотренной арки рационального очертания поперечная сила будет отлична от нуля, несмотря на равенство нулю изгибающего момента.
Это обстоятельство не препятствует определению внутренних усилий и расчету данного класса статически определимых систем на прочность.
2.Что касается перемещений, то в следующей главе будет показано, как перемещения в арке и в других стержневых системах можно найти, не обращаясь непосредственно к основным уравнениям строительной механики.
3.В этом пособии мы ограничимся рассмотрением эпюр внутренних усилий в арке как функций абсциссы х, а не длины дуги s. Отметим, что при этом, в отличие от рам, ось эпюры не совпадает с осью арки.
- 184 -
ГЛАВА 3. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СИСТЕМАХ
Если для расчета на прочность достаточно знания внутренних усилий, то расчет на жесткость требует умения определять перемещения системы. Это необходимо и для расчета на прочность статически неопределимых систем.
Напомним, что в сопромате мы находили линейные v и угловые θ перемещения балок с помощью интегрирования дифференциального уравнения изогнутой оси балки. Применить этот метод для определения перемещений в рамах практически невозможно: даже для простейшей П-образной рамы, показанной на рис. 2.6, это потребует решения трех дифференциальных уравнений – по одному для каждого участка рамы, и последующей стыковки полученных решений с учетом условий сопряжения в ее узлах. С увеличением числа стержней у рамы трудности будут быстро нарастать.
К счастью, для решения большинства задач в механике есть два подхода: первый основан на решении дифференциального уравнения, а второй – часто более эффективный – связан с использованием понятий «работа» и «энергия», к рассмотрению которых мы сейчас и приступаем.
3.1. Работа сил, приложенных к твердому телу
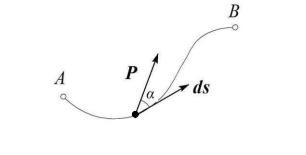
Рассмотрим точку M, которая перемещается по кривой АВ. Пусть P – сила, приложенная к точке, а ds – вектор элементарного перемещения, направленный по касательной к ее траектории (рис. 3.1).
M
Рис. 3.1
Определение. Элементарной работой силы P называется скалярное произведение вектора силы и вектора элементарного перемещения:
dA(P) = (P× ds) = Pcosα ds, |
(3.1) |
где α – угол между векторами P и ds.
Работа силы на конечном перемещении определяется как интеграл от элементарной работы силы:
В |
В |
|
A(P) = ∫ |
(P× ds) = ∫ Pcosα ds . |
(3.2) |
АА
- 185 -
Рассмотрим частные случаи применения этих формул.
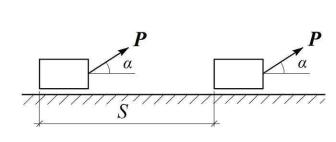
Работа постоянной силы на прямолинейном перемещении. Пусть век-
тор силы P остается постоянным по модулю и по направлению, и приложен к телу, перемещающемуся поступательно на расстояние S (рис. 3.2).
Рис. 3.2
В соответствии с формулой (3.2) работа силы будет равна:
|
S |
Pcosα ds = PS cosα . |
|
|
A (P) = ∫ |
(3.3) |
|
|
0 |
|
|
Очевидно, что: |
|
|
|
|
|
> 0, если 0 ≤ α< π/2; |
|
A (P) |
|
= 0, если α = π/2; |
|
|
|
< 0, если π/2 < α ≤ π. |
|
Отметим, что работа силы равна нулю, если сила перпендикулярна к перемещению точки ее приложения.
Работа силы при вращении тела. Рассмотрим тело, закрепленное на оси, перпендикулярной к плоскости чертежа и проходящей через центр О. Элементарная работа силы P, приложенной в точке А этого тела, при его повороте на угол dϕ (рис. 3.3) будет равна:
dA(P) = Pcosα ds = PcosαOAdϕ = M0 (P) dϕ.
Если вместо силы P к вращающемуся телу приложить момент M, результат не изменится. В самом деле, этот момент можно заменить парой сил (P, P′) с плечом h = OA cosα, равных по модулю P = P′= M/h, где сила P приложена в точке A, а P′– в центре О. Итак, элементарная работа сил при вращении тела равна:
dA = M0 dϕ, |
(3.4) |
где M0 – главный момент сил, приложенных к этому телу.

- 186 -
Рис. 3.3
Примечания
1.Работа момента (или пары сил), приложенных к твердому телу, движущемуся поступательно, то есть без вращения, равна нулю.
2.В самом общем случае можно рассмотреть движение в плоскости чертежа незакрепленного тела, загруженного произвольной системой сил. Приводя эти силы к произвольно-
му центру O этого тела, то есть, заменяя их главным вектором R0 и главным моментом M0, мы получим, что элементарная работа сил, приложенных к диску, при его перемещении будет равна:
dA = ( R0×ds0) + M0 dj,
где ds0 – элементарное перемещение центра О, а dj – элементарный поворот тела.
3. Размерность работы в соответствии с (3.3) равна произведению размерности силы на размерность перемещения:
[A] = [P]× [S] = Н× м = Дж.
3.2. Работа сил, приложенных к деформируемому телу
Работа упругой силы. Простейшей моделью деформируемого тела является обыкновенная пружина. Пусть ее левый конец закреплен, а правый – совпадает с началом системы координат Ox (рис. 3.4, а). Чтобы растянуть пружину с жесткостью c на длину x надо приложить внешнюю упругую силу P = cx, которая равна по модулю и направлена противоположно внутренней упругой силе
пружины Fупр = − P (рис. 3.4, б).
Вообще, в механике упругой называется сила, модуль которой пропорционален величине смещения точки ее приложения.
В нашем случае работа упругой силы P будет равна:
x |
x |
|
A (P) = ∫ |
Pdx = ∫ cxdx = cx2/2 = Px/2. |
|
0 |
0 |
|
Итак, работа упругой силы равна половине произведения максимального |
||
значения силы на величину вызванного ею перемещения: |
|
|
|
A (P) = Px/2. |
(3.5) |
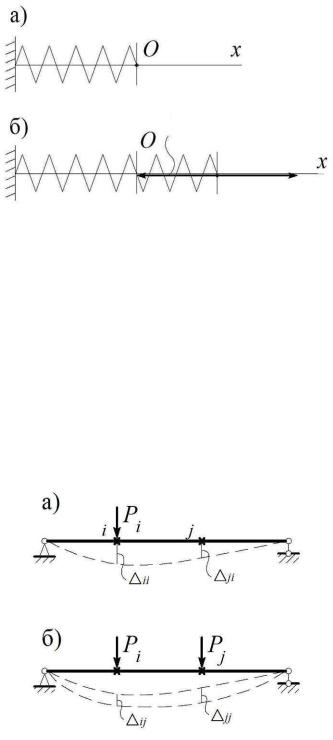
- 187 -
Fупр
Р
Рис. 3.4
Отметим, что работа внешней упругой силы положительна, а работа внутренней упругой силы Fупр = − P отрицательна: A (Fупр) = − A (P).
В дальнейшем работу внутренних сил деформируемого тела будем обозначать буквой W, а букву A сохраним для обозначения работы приложенных к нему внешних сил. При этом A = − W.
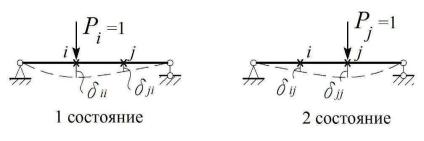
Работа сил при деформации упругого тела. Рассмотрим в качестве та-
кого тела простую двухопорную балку с зафиксированными на ней точками i и j (рис. 3.5, а).
Рис. 3.5
Приложим в точке i упруго, или статически силу Pi – эти термины означают, что в процессе загружения балки сила изменяет свою величину от нуля до максимального значения, которому соответствует изогнутая ось балки, показанная на рис. 3.5, а пунктиром. Обозначим через ii и ji перемещения точек i и j , вызванные силой Pi.
- 188 -
Зафиксируем силу Pi и дополнительно приложим к балке в точке j – тоже статически – силу Pj. Под действием последней точка i получит дополнитель-
ное перемещение ij, а точка j – дополнительное перемещение |
jj (рис. 3.5, б). |
Подсчитаем работу, совершенную этими силами при деформации балки: |
|
A (Pi) =1/2 Pi ii+ Pi ij; |
(3.6) |
A (Pj) =1/2 Pj jj. |
(3.7) |
Отметим, что на первом этапе загружения сила Pi является упругой, а балка играет роль пружины, поэтому первое слагаемое в (3.6) вычисляется по формуле (3.5). На втором этапе загружения Pi = const и ее работа вычисляется по формуле (3.3).
Таким образом, работа постоянной силы Pi на перемещении ij , вызванном «чужой» силой Pj, вычисляется без коэффициента 1/2.
Примечания
1. При деформации балки точки, лежащие на ее оси, получают не только линейные перемещения i (совпадающие с прогибами vi), но и угловые θi, поэтому если вместо упругой силы Pi в этой точке приложить упругий момент Mi, формула (3.6) примет вид:
A(Mi) = 1/2Miθii +Miθij ,
где θii – угол поворота сечения в точке i, вызванного упругим моментом Mi, а θij – угол пово-
рота сечения в точке i, вызванного силой Pj.
2. Напомним, что в общем случае перемещение всякой точки стержневой системы определяется тремя компонентами: ui, vi, θi – смотри уравнения 1.11 в §1.3. Обозначение i , введенное в этом параграфе, являются традиционными в строительной механике и применяются как для линейных, так и для угловых перемещений. Таким обобщенным перемещениям i соответствуют обобщенные силы: обычные P для линейных перемещений и моменты M – для угловых. При этом произведение обобщенной силы на обобщенное перемещение имеет размерность работы.
3. Как известно из курса физики, работа, совершенная внешними силами при деформировании упругого тела, равна потенциальной энергии, приобретенной этим телом.
3.3. Общие теоремы строительной механики
Теорема Бетти (о взаимности работ). Рассмотрим два состояния упру-
гой системы (рис. 3.6). Соответствующие им силы назовем силами первой и второй группы. Представим два варианта загружения балки.
Вначале статически приложим силы первой группы, затем их зафиксируем и добавим – также статически – силы второй группы. Очевидно, что процедура, показанная на рис. 3.5, является частным случаем рассматриваемой, по-

- 189 -
этому по аналогии с формулами (3.6) и (3.7) суммарную работу нагрузки можно представить в следующем виде:
AI = A11 + A12 + A22,
где A11 – работа первой группы сил на вызванных ими перемещениях;
A12 – работа первой группы сил на перемещениях, вызванных силами второй группы;
A22 – работа второй группы сил на вызванных ими перемещениях.
Рис. 3.6
Во втором варианте загружения вначале статически приложим силы второй группы, затем их зафиксируем и добавим силы первой группы. В этом случае суммарная работа сил будет равна:
AII = A22 + A21 + A11.
Работа сил, приложенных к идеально упругому телу, не зависит от истории загружения и определяется только начальным и конечным состоянием системы, поэтому, приравнивая AI и AII, получим:
A12 = A21 . |
(3.8) |
Итак, теорема Бетти утверждает, что работа первой группы сил на пере-
мещениях, вызванных силами второй группы, равна работе второй группы
сил на перемещениях, вызванных силами первой группы.
Поскольку работа внешних сил равна и противоположна по знаку работе внутренних сил: A = − W, теорема Бетти справедлива и для них:
W12 = W21 .
Отметим, что эта теорема является основной среди общих теорем строительной механики – две другие можно рассматривать как следствия теоремы Бетти.
- 190 -
Теорема Максвелла (о взаимности удельных перемещений). Рассмот-
рим два состояния упругой системы. Пусть первое из них представлено силой Pi = 1, приложенной в точке i , а второе – силой Pj = 1, приложенной в точке j
(рис. 3.7).
|
Pi =1 |
|
|
|
|
|
|
Pj =1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
δij |
|
|
|
|
|
|
|
δji |
|
|
|
|
|
|
|
|
δii |
|
|
|
|
δjj |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.7
Здесь и в дальнейшем удельные перемещения мы будем обозначать не заглавными буквами i, а строчными – δi .
Поскольку перемещение всякой точки упругой системы пропорционально приложенной силе, между ji на рис. 3.5, а и δji на рис. 3.7 существует зависимость: ji = Piδji или, сменив последовательность индексов на более привычную:
ij = Pj δij. |
(3.9) |
Воспользуемся теоремой Бетти, записав формулу (3.8) в виде:
Pi δij = Pjδji .
Учитывая, что в последнем выражении Pi = Pj = 1, получим:
δji = δij. |
(3.10) |
Итак, теорема Максвелла утверждает, что перемещение точки i от еди-
ничной силы, приложенной в точке j , равно перемещению точки j от единичной силы, приложенной в точке i.
Теорема Релея (о взаимности удельных реакций). Для СНС в качестве внешних сил, фигурирующих в теореме Бетти, могут выступать реакции, вызванные кинематическими воздействиями.
Рассмотрим два состояния упругой системы, где первое соответствует единичному смещению i-й моментной связи на левом конце балки, а второе – единичному смещению j-й линейной связи на ее правом конце. Обозначим че-
рез δij и θij линейное перемещение и угол поворота i-й связи от единичного смещения j-й связи (рис. 3.8).
