
10368
.pdf
31
|
m l (1 3 v2 ) |
m l (1 3 u2 ) |
|
|
|
32
3.4.Аналитические выражения для изгибающих моментов и поперечных сил в произвольном сечении неразрезной балки
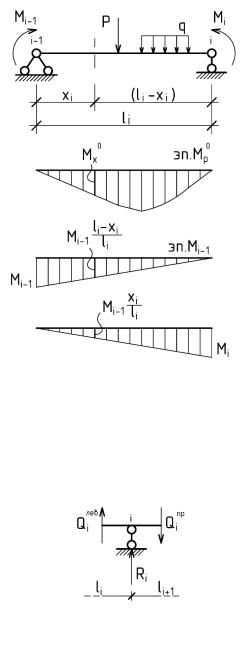
Для определения изгибающего момента Mx и поперечной силы Qx в произвольном сечении неразрезной балки необходимо рассмотреть один пролет как простую двухопорную балку, загруженную местной нагрузкой и найденными из решения канонических уравнений опорными моментами (реакциями в лишних связях).
В соответствии с принятыми правилами знаков:
-изгибающий момент считается положительным, если он вызывает растяжение нижних волокон балки;
-поперечная сила считается положительной, если она стремится оба участка балки, разделяемые рассматриваемым сечением, поворачивать по часовой стрелке.
На рис. 3.7 показан произвольный пролет неразрезной балки, загруженный местной нагрузкой в виде сосредоточенной силы и участка равномерно-распределенной нагрузки,
атакже найденными из решения канонических уравнений опорными моментами. Пусть оба опорных момента будут положительными.
Используя принцип независимости воздействий, построим эпюры изгибающих моментов в i-ом пролете от полученного загружения. Для произвольного сечения, отстоящего от левой опоры на расстоянии “x”, аналитическое выражение изгибающего момента примет вид:
Mx |
Mx0 |
Mi 1 (li xi ) Mi xi |
. |
|
|||
|
|
li |
|
Формула для поперечной силы в этом же сечении получается дифференцированием выражения изгибающего момента:
Qx |
Qx0 |
Mi Mi 1 |
. |
|
|||
|
|
li |
|
Опорная реакция на любой опоре i легко получается следующим способом: нужно вырезать дву мя сечениями, расположенными
Рис.3.7.
по обе стороны от опоры, бесконечно малый участок балки (см. рис. 3.8) и спроектировать на вертикаль все действующие на него силы. Будем считать
положительной реакцию, направленную вверх. Тогда,
приняв слева и справа от i-ой опоры поперечные силы положительные,
Рис 3.8
|
|
|
|
|
|
33 |
||
|
|
|
|
|
|
|
|
т.е. вращающие рассматриваемую отсеченную |
|
|
|
|
|
|
|
|
часть по часовой стрелке, получим: |
R Qпр. Qлев. R0 |
|
Mi 1 Mi |
|
Mi 1 Mi |
. |
|||
|
|
|||||||
i |
i |
i |
i |
|
li 1 |
|
li |
|
|
|
|
|
|
|
|||
В этом выражении Ri0 - реакция опоры i, которая возникает в ней в основной системе от заданной внешней нагрузки, расположенной на пролетах i и (i+1).
3.5. Замечания по выбору основной системы
Выше было отмечено, что в неразрезных балках с шарнирными крайними опорами или с консолями по концам количество неизвестных опорных моментов равно числу промежуточных опор, так как моменты на крайних опорах являются известными
величинами.
При жестко защемленных крайних опорах неизвестными являются моменты на промежуточных опорах, включая защемленные по концам опоры с примыкающими к ним дополнительными пролетами нулевой длины (см. рис. 3.9). Составляя для каждой промежуточной опоры уравнение трех моментов, получим совместную систему уравнений, решением которой определим неизвестные опорные моменты.
Рис 3.9
34
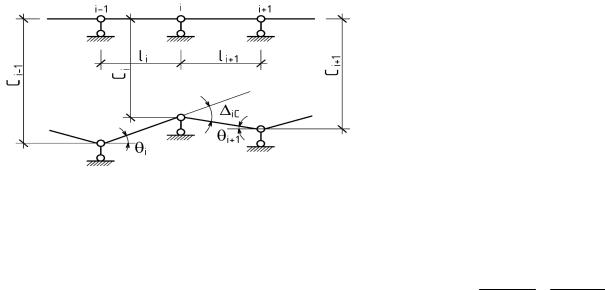
3.6.Расчет неразрезных балок на смещение опор
Внеразрезных балках, как в статически неопределимых системах, осадка опор вызывает отличные от нуля усилия.
При расчете на смещение опор каноническое уравнение метода сил принимает вид:
i1 x1 i2 x2 ... ik xk ic 0,
где ic - перемещение по направлению неизвестной xi , которое возникает в основной системе под влиянием смещения опор.
В применении к неразрезной балке, такое уравнение выражает равенство нулю перелома упругой линии на опоре, вызываемого совместным действием всех лишних неизвестных и перемещением опор.
Угол наклона пролета li, возникающий в основной системе от заданного смещения опор,
обозначим i , а пролета li+1 соответственно i 1
(см. рис. 3.10). Тогда: Таким образом, все эти углы легко определяются через заданное смещение опор. При этом осадки Ci 1,Сi ,Ci 1
считаются положительными при перемещениях, направленных вниз.
Уравнение трех моментов от осадки опор примет следующий вид:
Рис.3.10
i Mi 1 2 ( i i 1)Mi i 1 Mi 1
6 EI0 ( Ci 1 Ci Ci 1 Ci ) li
Если опоры сместятся таким образом, что все пролеты наклонятся одинаково, т.е.
окажется что 1 2 ... n , то все свободные члены уравнений обратятся в ноль, а
поэтому все изгибающие моменты также будут равны нулю. Этот вывод очевиден, так как при указанном условии все опорные точки останутся на одной прямой.
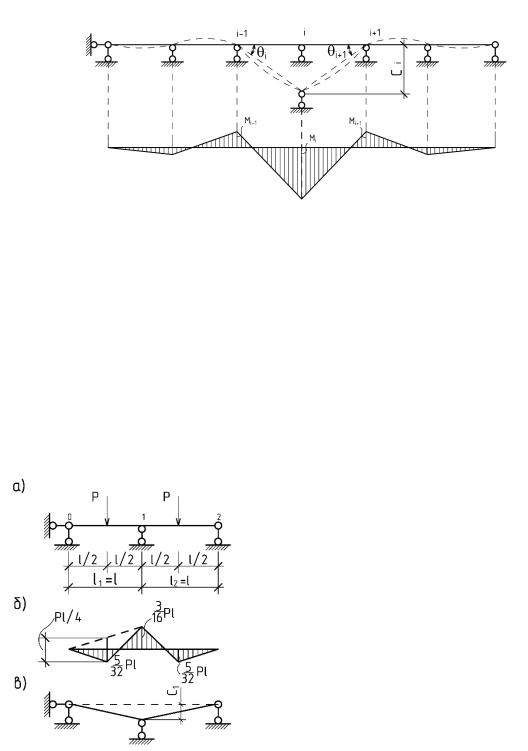
При любом сочетании смещений опор эпюра изгибающих моментов будет представлять собой ломаную линию с вершинами, расположенными на опорных вертикалях (см. рис. 3.11).
35
Рис 3.11
Смещение опор, которое происходит помимо требований проектировщика или строителя, является, несомненно, вредным фактором. Однако, сознательно вызывая смещение тех или иных опор, можно добиться определенных положительных результатов, например – выравнивание напряжений по длине балки.
Рассмотрим двухпролетную балку постоянного сечения, загруженную в середине пролетов двумя равными силами P (рис. 3.12). При не смещающихся опорах эпюра моментов будет иметь вид, показанный на рис. 3.12б, где момент на средней опоре будет
равен M |
1 |
|
3 |
|
Pl , а |
пролетные |
моменты |
под грузом |
Pl |
|
|
|
1 |
|
|
|
3 |
Pl |
5 |
Pl , |
|
т.е. по |
||||||||||||||||||||||||||||||
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
2 |
|
|
16 |
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
абсолютной величине пролетные моменты в 1,2 раза меньше опорного. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Поставим цель: выровнять пролетный и опорный |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
моменты по абсолютной величине, т.е. добиться |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
того, чтобы было |
Pl |
|
|
|
M1 |
M |
|
|
, или |
M |
|
|
Pl |
|
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Для |
этого |
|
нужно дать |
|
|
|
опорному |
|
моменту |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pl |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
PL |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
приращение |
M |
|
|
|
|
|
|
|
|
|
|
Pl |
|
|
|
|
|
. Этого |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
16 |
|
|
48 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
можно достигнуть, если опустить среднюю опору |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
на некоторую величину C1 (рис. 3.12в). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Значение этой величины найдем из уравнения |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
трех моментов, которое примет вид: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Рис 3.12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 C1 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 (l l |
|
) M 6 EI |
0 C1 |
|
|
|
, |
|
|
|
|
или, |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
l |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
учитывая значение M |
|
и что l l |
2 |
l : |
4 l |
Pl |
12 EI |
C1 |
. |
|
Отсюда вертикальная |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
48 |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
осадка средней |
опоры, |
|
при которой пролетные |
и опорный |
|
моменты |
будут |
|
равны, |
|||||||||||||||||||||||||||||||||||||||||||
составит: |
|
C |
|
P l3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
144 EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Задания для самостоятельной работы.
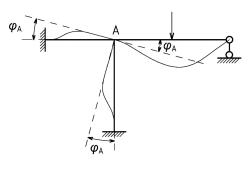
36
Литература: [1, гл. 5]; [2, гл. 6]; [4, гл. 4].
Вопросы для самопроверки:
1) Как определяется степень статической неопределимости для неразрезных балок? 2)Как записывается уравнение 3-х моментов при дейсткии нагрузки?
3)В чем заключается преимущество выбора основной системы по Клайперону? 4)Как записывается уравнение 3-х моментов при кинематическом воздействии?
4. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ ПЕРЕ-
МЕЩЕНИЙ
4.1. Общие сведения
Метод перемещений, наряду с методом сил, является одним из основных способов расчета статически неопределимых рам и, в настоящее время, получил большое распространение, особенно при расчете сложных статически неопределимых систем с большим количеством лишних связей, обладающих малой подвижностью узлов: сложные каркасные рамы, фермы с жесткими узлами и т.д.
При расчете систем по методу перемещений вводятся следующие предпосылки:
продольные (за исключением расчета на температуру) и сдвиговые деформации всех элементов рассматриваемой системы равны нулю. Отличны от нуля только деформации изгиба;
полагая деформации изгиба малыми величинами, будем считать, что расстояние между узлами стержня системы до и после деформации остается неизменным;
углы поворота всех стержней, сходящихся в жестком узле, равны. Углом поворота называют угол, на который поворачиваются касательные, проведенные к упругим линиям в
этом узле. Например, на рис. 4.1 углом поворота узла A будем называть угол A , общий для всех трех касательных, сходящихся в нем.
Эти предпосылки или допущения основаны на том, что в реальных стержневых системах, работающих в пределах упругих деформаций, перемещения малы в сравнении с основными размерами конструкции, поэтому их влиянием на изменение параметров системы можно пренебречь.
Рис. 4.1.
Первые две предпосылки дают возможность легко определить, могут ли центры узлов рамы перемещаться под действием внешней нагрузки. Если перемещения возможны,
то количество независимых геометрических параметров, характеризующих эти возможные перемещения, называют степенью линейной подвижности узлов рамы. При этом,
37
степень линейной подвижности узлов рамы всегда совпадает со степенью изменяемости ее шарнирной схемы.
Кроме линейной подвижности, имеет место и угловая подвижность узлов рамы вследствие образования упругих линий при изгибе стержней.
Если для какой-либо рамы, нагруженной внешней нагрузкой, удается найти линейные и угловые перемещения узлов, то после этого нетрудно определить и все усилия в стержнях.
Именно на этом и основан метод перемещений, в котором за основные неизвестные принимаются линейные и угловые перемещения узлов.
4.2.Степень кинематической неопределимости системы
(число неизвестных по методу перемещений)
Степенью кинематической неопределимости называют число всех возможных пе-
ремещений узлов заданной системы, знание которых позволяет определить ее деформированный вид и, следовательно, при применении закона Гука – усилия во всех стержнях.
Из определения ясно, что общее число неизвестных по методу перемещений “n” будет равно сумме неизвестных углов поворота всех жестких узлов рамы nуг. и неизвестных линейных перемещений узлов nл. , т.е. n nуг. nл. .
Число угловых перемещений узлов равно числу незакрепленных (свободных) жестких узлов.
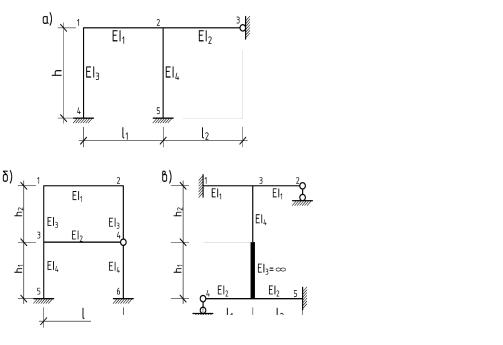
Например, для рам, изображенных на рис.4.2:
- для схемы а) – незакрепленными жесткими узлами являются узлы 1 и 2, т.е.
nуг. 2;
- для схемы б) |
- узлы 1, 2 |
и 3, т.е. |
|
|
nуг. 3; |
- для схемы в) - |
узел 3, т.е. nуг. |
1. |
Рис 4.2
Для определения числа возможных линейных перемещений узлов рамы или, иначе, степени их линейной подвижности, необходимо заданную систему заменить шарнирностержневой моделью путем введения в каждый жесткий узел полного шарнира. Тогда степень геометрической изменяемости полученной шарнирно-стержневой модели и будет выражать число возможных линейных перемещений узлов заданной системы.
38
Для рам степень геометрической изменяемости выражается формулой:
W 2 У С С0 ,
где: У - число узлов рамы; С – число
стержней; С0 – число опорных стержней (связей).
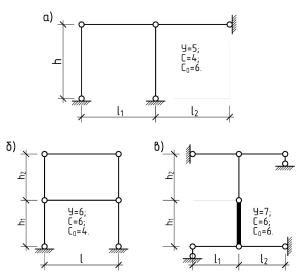
На рис. 4.3 показаны шарнирно-стержневые модели рам, соответственно изображенных на рис. 4.2. Степень их геометрической изменяемости равна:
-для схемы а): W 2 5 4 6 0;
-для схемы б): W 2 6 6 4 2;
-для схемы в): W 2 7 6 6 2.
Рис 4.3
4.3. Основная система метода перемещений
При расчете стержневых систем методом перемещений выбирают основную систему путем введения в заданную систему связей двух типов:
-моментных или угловых связей , препятствующих угловым перемещениям свобод-
ных жестких узлов заданной системы;
-силовых или линейных связей , препятствующих линейным перемещениям узлов шарнирно-стержневой модели заданной системы в направлении вводимых связей.
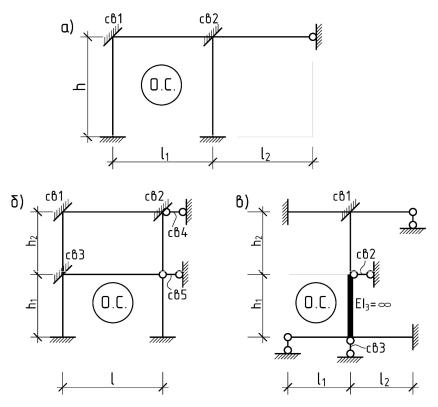
Так, например, для заданных систем по рис. 4.2 основные системы по методу перемещений будут иметь вид, изображенный, соответственно, на рис. 4.4.
При таком выборе основной системы последняя расчленяется на два типа стержневых элементов: стержневой элемент с двумя защемленными концами; стержневой элемент с одним защемленным и другим шарнирным концом.
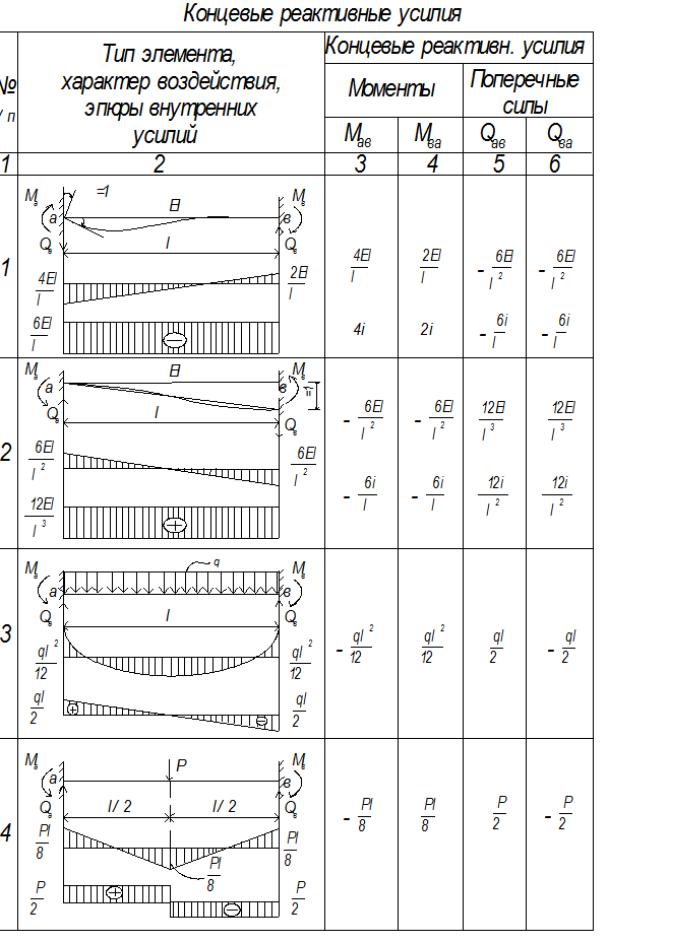
Каждый из этих типов стержневых элементов, вместе в определенном наборе составляющих основную систему для расчета заданной рамы по методу перемещений, может находиться под действием кинематических воздействий в виде угловых и относительных линейных перемещений концов, а также под действием приложенной к нему внешней нагрузки. Это дает возможность существенно упростить решение задачи, так как позволяет заранее подготовить расчеты приведенных выше двух типов стержневых элементов, а именно с использованием метода сил определить в них концевые реакции от кинематических воздействий и от нагрузки (см. табл. 4.1).
39
Рис. 4.4
40
Таблица 4.1.
