
10364
.pdf11
Способы решения этой более узкой задачи существенно различаются в зависимости от выбора основных неизвестных. Если основными неизвестными служат усилия в лишних связях, метод решения называют метод сил. Если основными неизвестными служат те или иные перемещения системы, являющиеся результатом ее деформации, метод расчета называют метод деформаций или метод перемещений. Если основными неиз-
вестными служат частью усилия в лишних связях, а частью перемещения, метод решения называют смешанный метод.
Задания для самостоятельной работы.
Литература: [1, гл. 5]; [2, гл. 6]; [4, гл. 4].
Вопросы для самопроверки:
1.Какие системы называют статически неопределимыми?
2.Какие методы используются для расчета статически неопределимых систем?
3.Как устанавливается степень статической неопределимости?
4.Какими свойствами обладают статически неопределимые системы?
2. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ СИЛ
2.1. Сущность метода сил
Одним из основных методов расчета статически неопределимых систем является метод сил. Сущность этого метода заключается в следующем:
-устанавливают общее число неизвестных, т.е. число лишних связей или степень статической неопределимости системы;
-устраняют (отбрасывают или перерезают) лишние связи, заменяя заданную (исходную) статически неопределимую систему основной статически определимой системой. Устранять можно только условно необходимые связи, чтобы основная система как в целом, так и в отдельных частях не оказалась геометрически изменяемой или мгновенно изменяемой;
-действие отброшенных связей заменяем в основной системе силами, которые и принимаем за основные неизвестные x1 , x2 , … , xn ;
-для основной системы составляют уравнения совместности перемещений (канонические уравнения метода сил), выражающие условия равенства нулю перемещений точек приложения каждого из неизвестных по направлению этих неизвестных.
Выбор лишних неизвестных определяет и выбор основной системы. Путем рационального выбора лишних неизвестных и, следовательно, основной системы, решение задачи может быть существенно упрощено.
2.2.Общая форма канонических уравнений метода сил для расчета на действие внешней нагрузки
Общую форму и смысл канонических уравнений метода сил рассмотрим на примере расчета статически неопределимой рамы, изображенной на рис. 2.1а, находящейся под действием внешней нагрузки.

|
|
12 |
|
|
|
|
|
|
|
|
|
|
Степень |
|
|
|
|
статической |
неопределимости |
||||
|
Л 3 1 0 3. |
На рис. 2.1б, |
в, г, д показаны |
||||||||
|
некоторые возможные основные системы, полученные |
||||||||||
|
из заданной путем устранения трех условно |
||||||||||
|
необходимых связей. В каждой из них действие |
||||||||||
|
отброшенных |
|
|
связей |
заменено |
силами |
– |
||||
|
неизвестными реакциями связей. Остановимся на |
||||||||||
|
основной системе по рис. 2.1б (в этой системе |
||||||||||
|
наиболее просто строятся эпюры изгибающих |
||||||||||
|
моментов от внешней нагрузки и от единичных |
||||||||||
|
значений |
лишних неизвестных). |
Работа основной |
||||||||
|
системы отличается от работы заданной. Чтобы |
||||||||||
|
деформации основной системы были такими же, как и |
||||||||||
|
заданной системы, необходимо, чтобы перемещение |
||||||||||
|
точек приложения неизвестных усилий по их |
||||||||||
|
направлениям от этих неизвестных и от заданной |
||||||||||
|
нагрузки равнялись бы нулю, т.е.: |
|
|
|
|||||||
|
xo |
(x , x |
2 |
, x |
3 |
, P) 0; |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
||
|
xo |
(x , x |
2 |
, x |
3 |
, P) 0: |
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
||
|
xo |
(x , x |
2 |
, x |
3 |
, P) 0, |
|
|
|
|
|
|
3 |
1 |
|
|
|
|
|
|
|
||
|
где |
xo - |
|
перемещение точки |
приложения |
||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
неизвестного xi |
по его направлению от действия сил |
|||||||||
|
x1 , x2 , x3 |
и заданной нагрузки P. |
Используя принцип |
||||||||
|
независимости действия сил, в развернутом виде |
||||||||||
|
уравнения запишутся в форме (для краткости, в |
||||||||||
|
индексах при перемещениях буква “x” опущена): |
|
|||||||||
|
011 012 013 01P 0; |
|
|
|
|
||||||
|
021 022 023 02P 0; |
|
|
|
|
||||||
|
031 032 033 03P 0. |
|
|
|
|
||||||
|
В этих выражениях 0ij - перемещение в основной |
|
|||||||||
Рис. 2.1 |
системе точки приложения неизвестного xi по его |
|
|||||||||
направлению от неизвестного xj , а 0iP - перемещение в основной системе точки
приложения неизвестного xi по его направлению от внешней нагрузки. |
|
||||
Для |
линейно-деформируемых |
упругих |
систем, |
используя |
принцип |
пропорциональности, запишем: 0ij ij |
xj , где |
ij - перемещение точки приложения |
|||
неизвестного xi по его направлению, вызванное |
действием силы xj = 1 |
(удельное |
|||
перемещение). Тогда в явной форме уравнения запишутся в следующем виде: |
|
||||
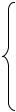
13
11 x1 12 x2 13 x3 01P 0;
21 x1 22 x2 23 x3 02P 0;
31 x1 32 x2 33 x3 03P 0.
Эта система называется системой канонических уравнений метода сил. Коэффици-
енты при неизвестных представляют собой удельные перемещения двух видов:
-ii - главные удельные перемещения;
-ij - побочные удельные перемещения (i j).
Эти перемещения определяются по формуле Мора-Максвелла:
|
|
|
|
|
|
|
|
___ |
___ |
|
|
|
|
___ |
|
|
|||
|
|
|
m |
|
|
l |
|
|
0 |
0 |
|
|
m |
l |
0 |
2 |
|
||
а) |
ii |
|
|
0 |
Mi |
Mi |
ds = |
|
0 |
[M i ] |
|
ds 0 - главные удельные перемещения всегда |
|||||||
|
|
|
|
|
|
|
EI |
|
|||||||||||
|
|
|
1 |
|
|
|
EI |
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
___ |
|
|
|
|
|
|||
положительны. Здесь Mi0 |
- изгибающий момент в основной системе от xi = 1; |
||||||||||||||||||
|
|
|
|
|
|
|
|
___ |
|
___ |
|
|
|
|
|
|
|
|
|
|
|
|
m |
l |
|
|
M 0 |
M 0 |
|
|
|
|
|
||||||
б) ij |
|
0 |
|
|
|
i |
|
j |
ds 0, 0 |
- |
побочные удельные перемещения. |
||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
EI |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
___ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь M 0j |
- изгибающий момент в основной системе от xj = 1; |
||||||
|
|
|
|
|
|
|
l |
___ |
|
|
|
|
|
|
|
|
|
||
|
|
|
m |
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|||
в) |
iP |
|
|
Mi |
MP |
ds 0, 0 |
грузовые перемещения или свободные члены канониче- |
||||||||||||
|
|
||||||||||||||||||
|
|
|
1 |
|
0 |
|
|
EI |
|
|
|
|
|
||||||
ских уравнений метода сил. MP0 - изгибающий момент в основной системе от заданной нагрузки. Таким образом, для определения удельных и грузовых перемещений необходимо в принятой основной системе построить эпюры моментов от единичных лишних неизвестных и от заданной нагрузки.
На рис. 2.2 показаны эпюры моментов от единичных лишних неизвестных и от нагрузки в принятой основной системе по рис. 2.1д.
14
а) |
б) |
в) |
г) |
Рис.2.2
Согласно теореме Максвелла, побочные удельные перемещения обладают свойст-
вом взаимности, т.е. ij ji . По построенным эпюрам в соответствии с формулами а), б)
и в) определяем коэффициенты при неизвестных в системе канонических уравнений метода сил и грузовые перемещения. Подставляя их значения в канонические уравнения метода сил и решая последние, определяем величины лишних неизвестных x1 , x2 , x3 .
Для построения эпюры моментов в заданной системе используем принцип независимости воздействий, справедливый для упругой линейно-деформируемой системы:
n
MP MP0
1
___
(Mi0 xi ). Для рассматриваемого примера формула примет вид:
M |
|
M0 |
___ |
___ |
x |
___ |
x |
|
p |
M0 |
x M0 |
M0 |
. |
||||
|
p |
1 |
1 2 |
2 |
3 |
3 |
|
Аналогично запишутся и выражения для поперечных и продольных сил:
Q |
|
Q0 |
___ |
|
___ |
x |
|
|
___ |
x ; |
|
|||
p |
Q0 |
x Q0 |
2 |
Q0 |
|
|||||||||
|
|
p |
1 |
1 |
2 |
|
|
3 |
|
3 |
|
|||
N |
|
|
N0 |
___ |
|
___ |
|
x |
|
___ |
x |
|
||
p |
N0 |
x N0 |
2 |
N |
0 |
, |
||||||||
|
p |
1 |
1 |
2 |
|
|
3 |
3 |
|
|||||
или, в общем виде:
15
|
n |
___ |
MP MP0 |
Mi0 xi ; |
|
|
1 |
|
|
n |
___ |
QP QP0 |
Qi0 xi ; |
|
|
1 |
|
|
n |
___ |
NP NP0 Ni0 xi .
1
В этих выражениях n – число лишних неизвестных или степень статической неопределимости системы.
2.3. Канонические уравнения для расчета на действие температуры
Как уже было сказано выше, в статически неопределимых системах от изменения температуры возникают внутренние усилия Mt , Qt и Nt .
Алгоритм расчета статически неопределимой системы от изменения температуры следующий:
-определяют число лишних связей или степень статической неопределимости заданной системы;
-выбирают основную систему, устраняя лишние связи и заменяя их действием лишних неизвестных;
-накладывают на основную систему требования, чтобы она работала как заданная,
т.е. чтобы перемещение точек приложения неизвестных усилий по их направлениям от
этих неизвестных и от температуры равнялись бы нулю, т.е.:
x1o(x1 , x2 ,..., xn , t) 0;x2o(x1 , x2 ,..., xn , t) 0;
. . . . . . . . . . . . . . . . . . . . .
xno(x1 , x2 ,..., xn , t) 0.
- используя принцип независимости воздействий и принцип пропорциональности, составляют канонические уравнения метода сил:
11 x1 12 x2 ... 1n xn 01t 0;
21 x1 22 x2 ... 2n xn 02t 0;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31 x1 32 x2 ... 3n xn 03t 0.
Коэффициенты при неизвестных – главные и побочные удельные перемещения в этих уравнениях определяются по тем же формулам, что и при расчете от нагрузки. Свободные члены канонических уравнений представляют собой перемещения точек приложения лишних неизвестных в основной системе по их направлениям от изменения температурного режима и определяются по формуле:
16
|
k |
l |
t |
___ |
k |
l |
___ |
|
0it |
|
Mi0 |
dS t0 Ni0 dS |
|||||
h |
||||||||
|
1 |
0 |
|
1 |
0 |
|
||
при условии постоянного изменения температуры по длине каждого стержня и однород-
ности материала.
Здесь
– коэффициент линейного расширения материала;
t0 |
|
(t1 |
t2 ) |
– приращение температуры по оси стержня; |
|
2 |
|||
|
|
|
|
t1 – приращение температуры наружных волокон;
t2 – приращение температуры внутренних волокон;
t t1 –t2 – перепад температур;
Н – высота сечения в плоскости изгиба ώ;
На практике слагаемое it определяют по формуле
|
|
m |
|
m |
t |
|
|
it |
t0 _ |
|
_ , где |
||
|
|
|||||
|
|
v 1 |
Ni0 |
v 1 |
H Mi0 |
|
_ |
– площади эпюр нормальных сил и изгибающих моментов на стержне с меняю- |
|||||
M i0 |
|
|
|
|
|
|
щейся температурой от силового фактора Хi =1;
m – число стержней, по длине которых происходит изменение температурного режима.
Каждое слагаемое считается положительным, если деформации, вызванные сило-
вым фактором Хi=1 и изменением температурного режима совпадают, и – отрицательным,
если эти деформации не совпадают.
2.4. Канонические уравнения для расчета рам на кинематические воздействия
Как уже было сказано выше, в статически неопределимых системах от кинематиче-
ских воздействий (осадка опор) возникают внутренние усилия Mc , Qc и Nc .
Алгоритм расчета статически неопределимой системы от осадки опор следующий:
-определяют число лишних связей или степень статической неопределимости заданной системы;
-выбирают основную систему, устраняя лишние связи и заменяя их действием лишних неизвестных;
17
- накладывают на основную систему требования, чтобы она работала как заданная,
т.е. чтобы перемещение точек приложения неизвестных усилий по их направлениям от этих неизвестных и от осадки опор равнялись бы нулю, т.е.:
x1o(x1 , x2 ,..., xn , с) 0;x2o(x1 , x2 ,..., xn , с) 0;
. . . . . . . . . . . . . . . . . . . . .
|
|
|
|
xo(x , |
x |
2 |
,..., x |
n |
, с) 0. |
||||||
|
|
|
|
n |
|
1 |
|
|
|
|
|
|
|
||
- используя принцип независимости воздействий и |
|||||||||||||||
составляют канонические уравнения метода сил: |
|
|
|
|
|
||||||||||
|
11 |
x |
|
12 |
x |
2 |
... |
1n |
x |
n |
0 |
||||
|
|
1 |
|
|
|
|
|
|
1с |
||||||
|
21 |
x |
|
22 |
x |
2 |
... |
2n |
x |
n |
0 |
||||
|
1 |
|
|
|
|
|
|
2с |
|||||||
принцип пропорциональности,
0;
0;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31 x1 32 x2 ... 3n xn 03с 0.
Коэффициенты при неизвестных – главные и побочные удельные перемещения в этих уравнениях определяются по тем же формулам, что и при расчете от нагрузки. Свободные члены канонических уравнений представляют собой перемещения точек приложения лишних неизвестных в основной системе по их направлениям от осадки опор и определяются по формуле:
w
iс rvi0cv , v 1
где rvi0 – реакция в связи, получившей кинематическое воздействие, от силового фактора
Хi=1; сv – величина кинематического воздействия; w – число опорных связей, получив-
ших кинематические воздействия.
Реакция rvi0 считается положительной, если ее направление совпадает с направле-
нием кинематического воздействия, и – отрицательной, если не совпадает.
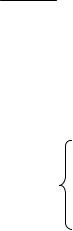
18
2.5. Упрощение канонических уравнений метода сил
Канонические уравнения в самом общем виде представляют собой систему линейных уравнений, решение которых не представляет принципиальных трудностей. Однако при большом числе уравнений решение связано с большим количеством вычислений и, в первую очередь, с вычислениями значительного количества главных и побочных удельных перемещений. Если степень статической неопределимости системы равна “n”, то общее число главных удельных перемещений равно то же “n”. Общее число побочных удельных перемещений равно n.(n-1). С учетом же теоремы о взаимности удельных пере-
мещений 12 21 , 13 31 и т. д. Отсюда общее число различных побочных удельных
перемещений составляет n (n 1) . 2
Поскольку (см. п. 2.2) побочные удельные перемещения могут быть положительными, отрицательными и равными нулю, то это их свойство дает возможность упростить канонические уравнения метода сил путем рационального выбора основной системы. При этом наиболее простое решение получается в том случае, когда все побочные удельные перемещения обращаются в ноль и канонические уравнения принимают вид
11 x1 01P 0;
22 x2 02P 0;
. . . . . . . . . . . . .
nn xn 0nP 0.
Вэтом случае удается полностью разделить неизвестные и получить ряд самостоятельных решений, каждое из которых содержит лишь по одному неизвестному.
2.5.1.Симметричные системы
Симметричными будем называть такие системы, которые удовлетворяют следующим условиям:
-геометрическая схема системы симметрична, т.е. имеет одну или несколько осей симметрии;
-опорные закрепления и узловые сопряжения элементов системы симметричны относительно оси (осей) симметрии;
-жесткости элементов, симметрично расположенных относительно оси (осей) симметрии системы, равны.
Пример симметричной статически неопределимой рамы показан на рис. 2.5.
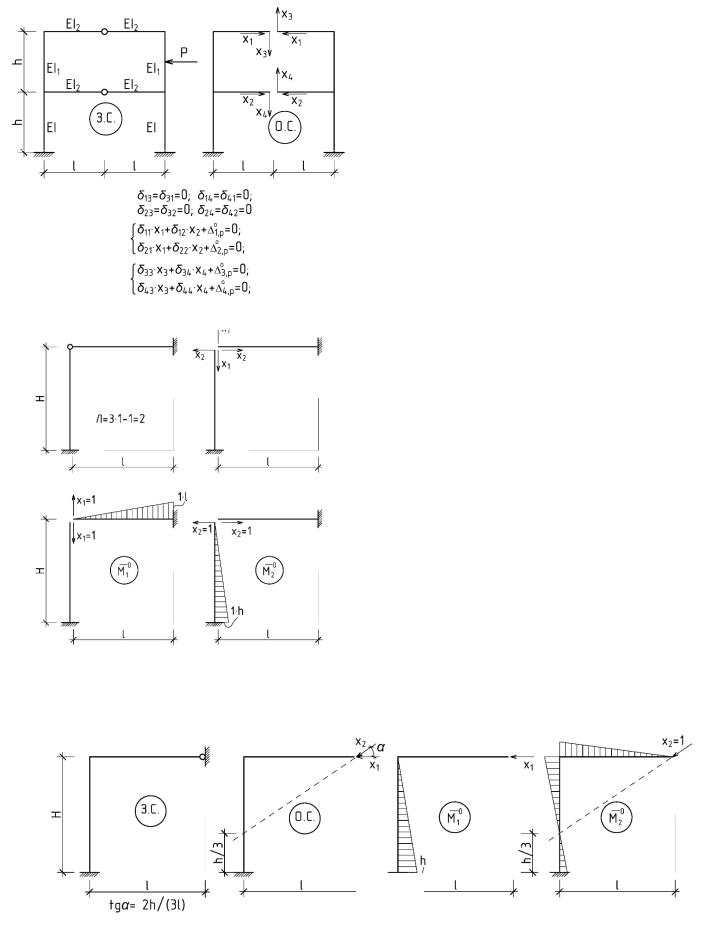
Рис 2.5
Рис 2.6
19
При расчете симметричных систем основную систему целесообразно выбирать так же симметричной, поскольку в этом случае часть побочных удельных перемещений обращается в ноль. Рассмотрим пример, изображенный на рис. 2.5. Имеем систему четыре раза статически неопределимую. Основную систему принимаем симметричную, проводя разрезы ригелей по оси симметрии. В этом случае вместо системы четырех канонических уравнений с четырьмя неизвестными получаем разделение неизвестных, что приводит к двум системам (группам)
уравнений. В первую группу урав нений
входят симметричные неизвестные x1 и x2, а во вторую – обратно симметричные неизвестные x3 и x4 .
Из этого примера наглядно следует, что:
перемножение симметричных и обратно симметричных эпюр всегда дает ноль, или иначе, эпюры являются взаимно нулевыми или ортогональными.
Существует три признака ортогональности эпюр:- в симметричных системах симметричные и обратно симметричные эпюры ортогональны;- две эпюры со взаимно безэпюрными участками ортогональны (см. рис. 2.6); - если под центром тяжести одной эпюры
расположена нулевая ордината в другой эпюре, то такие эпюры ортогональны (см. рис. 2.7).
рис.2.7
20
Дальнейшее упрощение при расчете симметричных систем имеет место тогда, когда и часть грузовых перемещений или свободных членов канонических уравнений также обращается в ноль. Рассмотрим симметричную систему, изображенную на рис. 2.8
инаходящуюся под действием следующих загружений:
-первый вариант – нагрузка по рис. 2.8a;
-второй вариант – нагрузка по рис. 2.8b.
|
При |
загружении |
системы нагрузкой по первому варианту |
будем |
иметь: |
|
12 |
21 0; |
02P 0 |
(в |
соответствии с признаками ортогональности |
эпюр: |
эп.MP0 |
|
|
|
|
___ |
|
|
обратно симметричная, а эп. M20 - симметричная). Тогда канонические уравнения примут |
||||||
вид: 11 x1 01P 0, а неизвестное x2 обратится в ноль. |
|
|
||||
|
При |
загружении |
системы нагрузкой по второму варианту |
будем |
иметь: |
|
12 |
21 0; |
01P 0 |
(в |
соответствии с признаками ортогональности |
эпюр: |
эп.MP0 |
___
симметричная, а эп. M10 - обратно симметричная). Тогда канонические уравнения примут вид: 22 x2 02P 0, а в ноль обратится неизвестное x1.
Выводы приведенного примера выражают собой следующую общую теорему:
при действии на симметричное сооружение симметричной нагрузки все обратно симметричные неизвестные обращаются в ноль. При действии на симметричное сооружение обратно симметричной нагрузки в ноль обращаются все симметричные неизвестные.
При действии на симметричную систему нагрузки произвольного вида, последнюю всегда можно представить в виде двух вариантов загружений – симметричного и обратно симметричного. Решение системы от каждого загружения отдельно приводит к существенному упрощению вычисления неизвестных канонических уравнений, так как при симметричной основной системе вследствие ортогональности эпюр часть побочных удельных перемещений и свободных членов уравнений обратятся в ноль.
Примеры разложения произвольной нагрузки, действующей на симметричную раму, на симметричную и обратно симметричную, показаны на рис. 2.9.
