
10315
.pdf
[Введите текст]
Из рисунков видно, что в случае правой тройки {a,b,c} вектор d a b об-
разует с вектором c острый угол q , а в случае левой тройки – этот угол тупой. С учетом того, что
a b,c | d | | c | cos q,
мы получим, что в первом случае знак смешанного произведения будет положительным, а во втором – отрицательным. Таким образом, знак смешанного произведения «говорит» о взаимной ориентации тройки векторов в пространстве.
А что означает равенство нулю смешанного произведения? Очевидно, что это будет тогда и только тогда, когда cos q 0 , т.е. q / 2 и, следова-
тельно, вектор c должен лежать в плоскости векторов a и b . Итак, обращение в нуль смешанного произведения эквивалентно компланарности данной тройки векторов.
900
Рис. 8.8
Теперь, что касается модуля смешанного произведения. Рассмотрим рисунок
Рис. 8.9
60

[Введите текст]
и запишем
| a b,c | | a | | b | | sin | | c | | cos q| S h V
где V – объем параллелепипеда, построенного на векторах a , b , c .
Итак, смешанное произведение некомпланарных векторов по модулю равно объему параллелепипеда, построенного на этих векторах.
Нам осталось только научиться вычислять смешанное произведение векторов, заданных своими координатами. Пусть
a ax , ay , az , b bx ,by ,bz , с {cx ,cy ,cz }.
Тогда
d a b |
i |
|
|
j |
|
k |
|
|
|
ay |
az |
|
|
a |
x |
a |
z |
|
ax |
ay |
|
||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
a |
|
a |
|
a |
|
|
i |
|
j |
|
k |
|
|||||||||||||||
x |
y |
z |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
by |
bz |
|
|
bx |
bz |
|
bx |
by |
|
||||||
|
|
bx |
by |
bz |
|
|
|
|
|
|
|
||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d ,c i |
|
ay az |
|
j |
|
ax |
az |
|
k |
|
ax ay |
|
, cxi cy j czk |
||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
by |
bz |
|
|
bx bz |
|
|
bx by |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
a2 |
a3 |
|
a1 a3 |
|
a1 a2 |
|
|
ax |
ay |
az |
||
|
|
|
|
||||||||||
c |
c |
c |
|
|
b b b |
||||||||
1 |
b b |
2 |
b b |
3 |
b b |
|
|
x |
y |
z |
|||
|
2 |
3 |
|
1 |
3 |
|
1 |
2 |
|
|
cx |
cy |
cz |
|
|
|
|
|
|
|
|
|
|
|
|||
Итак, мы получили выражение смешанного произведения через координаты сомножителей
ax ay aza b,c bx by bz .
cx cy cz
Следовательно, объём параллелепипеда, построенного на векторах a , b , c вычисляется по формуле
ax ay az V | bx by bz | .
cx cy cz
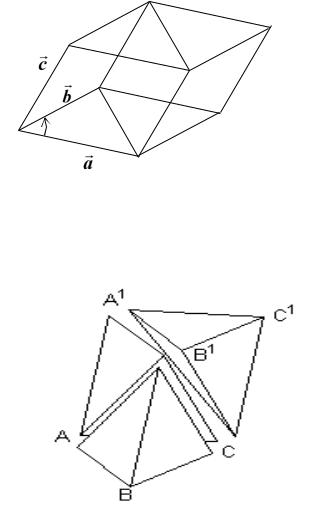
Часто возникает задача вычисления объема пирамиды по координатам ее вершин. Сведем эту задачу к вычислению объема параллелепипеда. Для этого разделим параллелепипед диагональным сечением на две равновеликих призмы
61
[Введите текст]
Рис. 8.10
В свою очередь каждую из полученных призм можно разделить на три равновеликих пирамиды.
Рис. 8.11
Таким образом, объем пирамиды равен |
1/ 6 |
от объема параллелепипеда, |
|||||
построенного на этих же векторах, т.е. |
|
|
|
|
|
|
|
|
1 |
|
a1 |
a2 |
a3 |
|
|
|
|
|
|||||
V |
| |
b |
b |
b |
| . |
||
|
|||||||
пир |
6 |
|
1 |
2 |
3 |
|
|
|
|
c1 |
c2 |
c3 |
|
||
|
|
|
|
||||
В заключение этой темы обратимся к геометрической интерпретации однородных систем линейных уравнений. Однородная система линейных уравнений всегда совместна, поскольку ранг расширенной матрицы совпадает с рангом основной матрицы. Одно из её решений очевидно. Это нулевое решение. Его называют тривиальным. Естественно возникает вопрос о существовании других решений. В «солидных» курсах алгебры доказывается, что для существования нетривиальных решений необходимо и достаточно, чтобы определитель системы однородных уравнений был равен нулю. Это утверждение становится очевидным (в трёхмерном случае), если сформулировать задачу на «языке» векторной алгебры.
Действительно, так как линейное уравнение вида a1x1 a2 x2 a3 x3 0
62

[Введите текст] |
|
|
|
|
|
|
|
|
означает, что скалярное |
произведение |
векторов |
a a1,a2 ,a3 и |
|||||
x x1, x2 , x3 равно нулю, т.е. они ортогональны, то решить систему |
||||||||
a1x1 a2 x2 a3 x3 0 |
|
|||||||
|
|
|
b2 x2 |
b3 x3 |
0 |
|
||
b1x1 |
(8.2) |
|||||||
c x c x c x 0 |
|
|||||||
|
1 |
1 |
2 |
2 |
3 |
3 |
|
|
это, значит, найти такой вектор x x1, x2 , x3 , который был бы перпендикулярен к трём векторам
a a1,a2 ,a3 , b b1,b2 ,b3 , c c1 ,c2 ,c3 .
Очевидно, что такой ненулевой вектор x существует тогда и только тогда, когда векторы a, b, c лежат в одной плоскости, то есть они компланарны. А равенство нулю определителя этой системы
a1 |
a2 |
a3 |
|
b1 |
b2 |
b3 |
0 |
c1 |
c2 |
c3 |
|
и есть условие компланарности этих векторов.
Раздел 3. Аналитическая геометрия. Прямые и плоскости
Лекция 9. Прямая линия на плоскости
Любая точка на плоскости однозначно определяется упорядоченной парой чисел – ее декартовыми координатами. Также и вектор на плоскости задается парой своих декартовых координат. В этой и ближайших лекциях мы получим аналитические представления для таких геометрических объектов, как прямая на плоскости, плоскость и прямая в пространстве.
9.1. Общее уравнение прямой. Пусть на плоскости с декартовой прямоугольной системой координат проведена прямая L , и мы хотим получить уравнение, связывающее координаты любой точки, принадлежащей этой прямой.
63

[Введите текст]
|
|
|
|
|
|
Рис. 9.1 |
|
|
Для этого зафиксируем какую-нибудь точку |
M 0 (x0 , y0 ) L и возьмем век- |
|||||||
тор N A, B , перпендикулярный (ортогональный, нормальный) |
к этой |
|||||||
прямой L . Очевидно, |
что для произвольной точки M (x, y) L векторы |
|||||||
|
|
|
|
|
|
|
||
|
M0M x x0 ; y y0 |
и |
N перпендикулярны, т.е. их скалярное произве- |
|||||
|
|
|
|
|
|
|||
дение обращается в ноль |
N, M0M 0 |
или в координатах |
|
|||||
|
|
|
|
A(x x0 ) B( y y0 ) 0 |
(9.1) |
|||
Таким образом, уравнение (9.1) – уравнение прямой L , проходящей через заданную точку M 0 (x0 , y0 ) перпендикулярно заданному вектору
N A, B .
Раскрывая в (9.1) скобки, получим уравнение
Ax By C 0 , |
(9.2) |
где для краткости обозначено C Ax0 By0 .
Уравнение (9.2) называют общим уравнением прямой на плоскости. Обратим внимание, что уравнение прямой на плоскости является линейным
уравнением относительно переменных x |
и y , а коэффициенты при них – |
|||||
соответствующие |
координаты нормального |
к |
этой |
прямой вектора |
||
N A, B . |
|
|
|
|
|
|
Обратно, покажем, что уравнение вида |
(9.2) |
определяет прямую на |
||||
плоскости и построим эту прямую. |
По данным числам |
A и B образуем |
||||
вектор N A, B |
и введём вектор r x, y . Тогда уравнение (9.2) можно |
|||||
представить в виде |
N,r C 0 |
или |
| N | ПрN r C . Отсюда |
|||
Пр N r C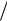 | N |,
| N |,
64

[Введите текст]
т.е. все радиус-векторы r x, y , координаты которых удовлетворяют уравнению (9.2), имеют одну и ту же проекцию на фиксированный вектор N A, B . Это означает, что точки M ( x, y ) принадлежат прямой, перпендикулярной вектору N A, B и отстоящей от начала координат на расстояние | p |, где
p |
C |
|
|
|
C |
|
. |
| N |
| |
|
|
|
|||
|
|||||||
|
|
|
A2 B2 |
||||
Отсюда следует алгоритм построения прямой по заданному уравнению (9.2). Через начало координат проведем прямую в направлении вектора
N A, B |
и отложим на ней от начала координат отрезок длиной |
N A, B |
в направлении вектора N A, B , если p 0 , или в противо- |
положном направлении, если p 0 . Через конец P этого отрезка проводим перпендикулярно ему требуемую прямую L .
N
 O L
O L
Рис. 9.2
Построение прямой производится гораздо проще, если воспользо-
ваться так называемым уравнением прямой в отрезках
x |
|
y |
1, |
(9.3) |
|
a |
b |
||||
|
|
|
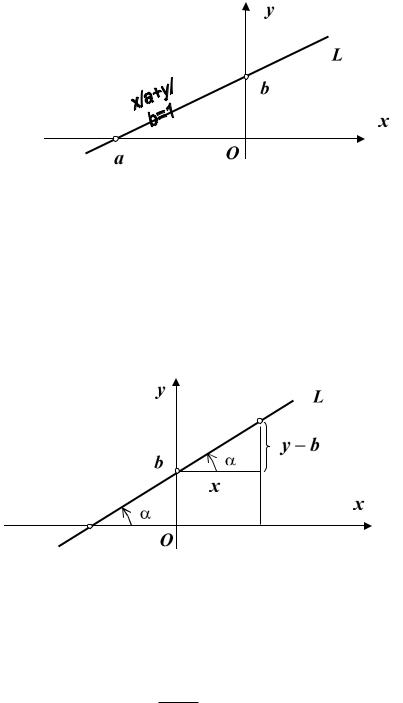
где (a,0) и (0,b) – точки пересечения прямой L с осями абсцисс и ординат,
соответственно.
Действительно, из (9.2) следует Ax By С и далее, предполагая, что A 0, B 0,C 0 (т.е. прямая не проходит через начало координат и не параллельна координатным осям) и разделив обе части этого уравнения на
C , получим уравнение (9.3), в котором a |
C |
и b |
C |
величины от- |
|
A |
A |
||||
|
|
|
резков, которые прямая «отрезает» от осей координат (см. рис. 9.3).
65
[Введите текст]
Рис. 9.3
9.2. Уравнение прямой с угловым коэффициентом. Иногда уравне-
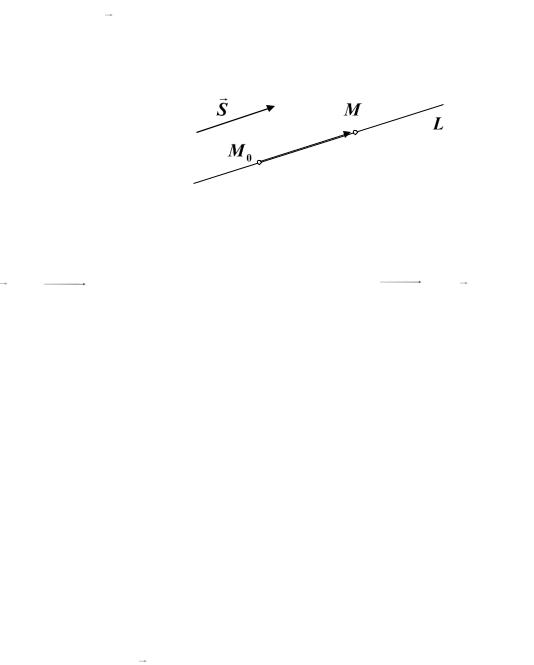
ние прямой удобно представить в другом виде. Пусть прямая L пересекает ось ординат в точке (0,b) и образует с положительным направлением оси
абсцисс угол , тангенс которого обозначим через k tg .
Рис. 9.4
Из рисунка следует, что для любой точки M (x, y) L выполняется равен-
ство
y b tg k , x
из которого следует уравнение прямой с угловым коэффициентом
y kx b . |
(9.4) |
Пусть точка M 0 (x0 , y0 ) L , тогда y0 kx0 b . Выражая отсюда b и
подставляя в (9.4), получим уравнение прямой с угловым коэффициентом k , проходящей через заданную точку, в виде
66
[Введите текст]
y y0 k (x x0 ) . |
(9.5) |
Заметим, что меняя в уравнении (9.5) величину k , мы получим множество прямых, проходящих через данную точку. Это множество прямых называется пучком прямых, проходящих через заданную точку.
9.3. Параметрические и каноническое уравнения прямой. Уравне-
ние прямой L можно получить, задавая точку M 0 (x0 , y0 ) и её направляю-
щий вектор S {m, n} (см. рис. 9.5).
Рис. 9.5
Пусть M (x, y) L – произвольная точка. В силу коллинеарности векторов
S и M0M x x0; y y0 |
имеем равенство M0M t S . В координатах |
||
это равенство примет вид |
|
|
|
x x0 |
m t |
t . |
(9.6) |
|
|
||
y y0 n t |
|
|
|
Это так называемые параметрические уравнения прямой. Ясно, что при изменении значения параметра t в пределах от до точка M (x, y)
«пробегает» всю прямую |
L . Очевидно, что точке M 0 (x0 , y0 ) |
соответствует |
||||
значение параметра t 0 . |
Исключая из этих уравнений параметр t , полу- |
|||||
чим каноническое уравнение прямой на плоскости |
|
|||||
|
|
x x0 |
|
y y0 |
. |
(9.7) |
|
|
|
|
|||
|
|
m |
n |
|
||
В частности, если одна из координат направляющего вектора равна |
||||||
нулю, например, S {m,0}, то получаем уравнение прямой |
y y0 . |
|||||
В качестве следствия из уравнения (9.7) получим уравнение прямой, |
||||||
проходящей через две заданные точки |
M1 (x1, y1 ) и M 2 (x2 , y2 ) . Как из- |
|||||
вестно, прямая определяется двумя своими точками. Нетрудно понять, что вектор
67

[Введите текст]
M1M2 x2 x1; y2 y1
можно считать направляющим вектором данной прямой. Отсюда получим
уравнение прямой, проходящей через две заданные точки
x x1 |
|
y y1 |
. |
|
|
||
x2 x1 |
|
y2 y1 |
|
Лекция 10. Прямые линии на плоскости
10.1. Взаимное расположение двух прямых. Пусть сначала две пря-
мые заданы уравнениями с угловым коэффициентом:
y k1x b1, |
y k2 x b2 . |
|
Найдем наименьший положительный угол между прямыми L1 и L2 . |
||
y |
|
L2 |
|
|
|
|
|
|
|
|
L1 |
|
68 |
|
|
||
O |
x |
[Введите текст]
Рис. 10.1
Пусть 1 и 2 — углы между положительным направлением оси Ox и прямыми L2 и L2 соответственно. Тогда 2 1 (внешний угол треуголь-
ника равен сумме внутренних углов, с ним не смежных). Отсюда следует,
что 2 1 ,
tg tg |
2 1 |
|
|
tg 2 tg 1 |
. |
|||||
|
|
|||||||||
|
|
|
1 |
tg tg |
2 |
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
Так как |
|
|
|
|
|
|
|
|
|
|
tg 1 k1 , |
tg 2 k2 , то |
|
|
|
|
|||||
tg |
|
k2 k1 |
. |
|
|
|
|
(10.1) |
||
|
|
|
|
|
|
|||||
|
1 k1 k2 |
|
|
|
|
|
||||
По этой формуле вычисляется положительный угол |
, |
который отсчиты- |
||||||||
вается от прямой y k1x b1 до прямой |
y k2 x b2 . |
Поскольку тангенс |
||||||||
этого угла может быть и отрицательным, то угол между прямыми равен
| arctg |
k1 k2 |
| . |
|
||
|
1 k1k2 |
|
Иногда по заданному углу между прямыми и известному угловому коэффициенту одной из прямых нужно найти угловой коэффициент другой прямой. Поэтому нужно быть внимательными при применении формулы (10.1). Чтобы подчеркнуть, какой угол вычисляется по этой формуле, в ней ставят стрелку, показывающую, что угол отсчитывается от прямой с угло-
вым коэффициентом |
k1 до прямой с угловым коэффициентом k2 . |
||
Пример. |
В |
плоскости луч |
света направлен по прямой |
L1 : x 2 y 5 0 |
и дойдя до прямой |
L2 : 3x 2 y 7 0 от неё отразился. |
|
Получить уравнение прямой, по которой направлен отражённый луч.
3 |
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
4 |
|
||
Вычисляем тангенс угла «падения» tg |
2 |
2 |
|
|
|
(см. рис. 10.2) |
||||||
|
3 |
1 |
|
7 |
||||||||
1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||
2 |
2 |
|
|
|
|
|||||||
69
