
10292
.pdfРассмотрим стационарную точку (x0 , y0 ) функции z f (x, y) , |
т.е. |
точку в которой обращаются в нуль обе частные производные f x и |
f y . |
Вычислим вторые производные в этой точке и введём, для краткости, следующие обозначения:
|
2 f (x , y |
) |
A, |
2 |
f (x , y |
) |
B, |
2 f (x , y |
) |
C . |
||||
|
0 |
0 |
|
|
0 |
0 |
|
0 |
0 |
|
||||
|
x2 |
|
|
|
|
x y |
|
|
|
y2 |
|
|
|
|
Примем без доказательства следующее правило: |
|
|
|
|
||||||||||
если в стационарной точке выполняется неравенство |
AC B2 0 |
|||||||||||||
, то в этой точке функция z f ( x, y) |
имеет экстремум;при этом, если |
|||||||||||||
A 0 , то f ( x0 , y0 ) – максимум, если |
A 0 , |
то f ( x0 , y0 ) – минимум |
||||||||||||
если в стационарной точке AC B2 0,то функция не имеет |
||||||||||||||
экстремума в этой точке |
|
|
|
|
|
|
|
|
|
|
||||
случай |
AC B2 |
0 требует дополнительного исследования. |
||||||||||||
Пример 1.Исследовать на экстремум функцию |
|
|
|
|
||||||||||
|
|
|
|
z 5 2x 6 y 2xy x2 . |
|
|
|
|
||||||
Находим стационарные точки, решая систему |
|
|
|
|
||||||||||
|
zx |
2 2 y 2x 0 |
|
M0 (3, 4) . |
|
|
|
|||||||
|
|
z |
|
6 2x |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y |
|
|
|
|
|
|
|
|
|
|
|
||
Вычисляем вторые производные в этой точке: |
A 2, |
B 2, |
C 0 . |
|||||||||||
AC B2 4 0 , поэтому экстремума нет. |
|
|
|
|
|
|
||||||||
Лекция 39. Условный экстремум
39.1. Понятие условного экстремума. Весьма часто возникает задача не просто найти экстремум функции n переменных u f (x, y,...) , а найти её
экстремум при дополнительных условиях, связывающих переменные посредством m уравнений связей ( m n )
gk (x, y,...) 0, k 1,..., m .
Такие экстремумы называют условными. Например, пусть требуется найти минимум функции
f (x, y) x2 y2
280
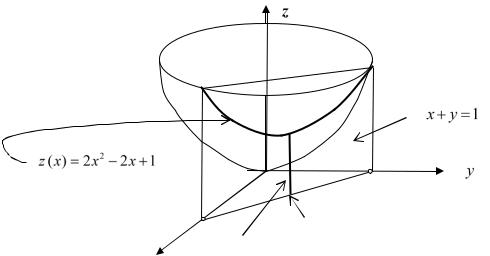
при дополнительном условии x y 1. Следующий рисунок делает решение задачи очевидным.
1
1
zmin 0, 5
x
(0,5;0,5)
Рис. 39.1
С учётом уравнения связи мы на самом деле имеем функцию одной переменной
f(x, 1 x) 2x2 2x 1
иеё экстремум легко находится. Следовательно, функция
f (x, y) x2 y2
имеет условный минимум fmin 0,5 в точке |
(0,5; 0,5) . |
Таким образом, задача нахождения условных экстремумов не является |
|
принципиально новой. Разрешая уравнения |
связи относительно m |
неизвестных и подставляя их в исходную функцию, мы получаем задачу отыскания безусловного экстремума функции меньшего ( n m) числа
переменных. Если задача разрешения уравнений связи не вызывает трудностей, то так и следует поступать. Но весьма часто это либо трудоёмкая задача, либо принципиально неразрешимая (вспомним, что не всегда можно перейти от неявного задания функции к её явному заданию).
39.2. Метод множителей Лагранжа. Представляется важным найти некоторую универсальную формулировку необходимых условий условного экстремума. Такая формулировка была предложена французским учёным Лагранжем (1736–1813 гг.).
Пусть требуется найти экстремумы функции
281

u f (x1, x2 , ... , xn ) ,
причём её n аргументов подчинены m уравнениям связей ( m n ) :
gk (x1, x2 , ... , xn ) 0, k 1, ... , m .
Введём |
m |
так называемых неопределённых множителейЛагранжа |
1, 2 , |
, m |
и образуем функцию Лагранжа |
|
|
F f 1g1 2 g2 ... m gm . |
Эта функция зависит от n mпеременных: x1, ... , xn , 1 , ... , m . Запишем для нее необходимые условия экстремума
F |
0 ,…, |
F |
0, |
F |
0 ,…, |
F |
0 . |
(39.1) |
x1 |
xn |
|
|
|||||
|
|
1 |
|
m |
|
|||
Заметим, что последние m уравнений в (39.1) совпадают с уравнениями связей. Оказывается, что необходимые условия экстремума функции Лагранжа являются одновременно необходимыми условиями условного экстремума исходной функции.
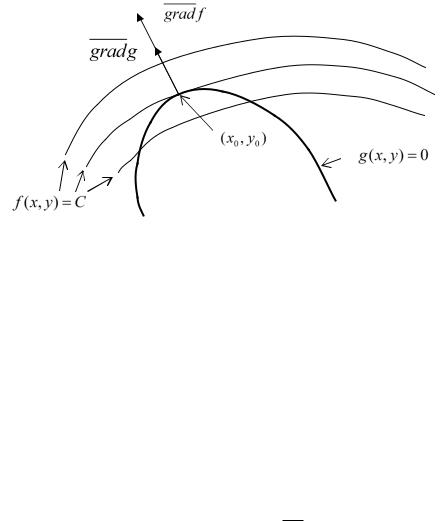
Чтобы в какой-то мере «оправдать» метод множителей Лагранжаограничимся нахождением экстремума функции двух переменных с одним уравнением связи. Допустим, что уравнение связи g(x, y) 0 изображается гладкойкривой, т.е. кривой, в каждой точке
которой существует касательная. Мы должны найти экстремум функции
z f (x, y) , |
когда точки (x, y) |
лежат на этой кривой. Двигаясь вдоль кривой |
|
g(x, y) 0 , |
например, слева |
направо, мы |
последовательно пересекаем |
линии уровня f (x, y) C . В точке (x0 , y0 ) , |
где кривая g(x, y) 0 касается |
||
одной из линий уровня f (x, y) C* , следует ожидать максимума, т.к. при переходе через эту точку возрастание C сменяется убыванием.
282

Приравнивая к нулю её частные производные, получаем следующую систему для нахождения координат стационарных точек
|
x (5x 3y) 0 |
|
||||
|
y ( 3x 5 y) 0 |
|
||||
|
|
|||||
|
5x |
2 |
6xy 5 y |
2 |
32 |
0 |
|
|
|
||||
Исключаем из первых двух уравнений параметр , разделив одно из них на другое
|
|
|
|
k 3 5k , |
k |
y0 |
. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
5 3k |
|
x0 |
|
|
|
|
|||||||||
Откуда |
k 1 или y0 |
x0 . Третье уравнение системы даёт возможность |
||||||||||||||||||||
найти |
конкретные значения координат стационарных точек. В случае |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y0 |
x0 |
находим точки |
( 2 |
|
2; 2 2; 0,5 ), ( 2 2; 2 |
|
2; 0,5 ) . А если |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
y0 |
x0 , то получаем точки |
( 2; |
|
2; 1 |
8 ) , ( 2; |
2; 1 8 ) . |
||||||||||||||||
|
Мы не касаемся вопроса о достаточных условиях экстремума в общем |
|||||||||||||||||||||
случае. Его исследование завело бы нас слишком далеко. Как и в случае безусловного экстремума, в практических приложениях обыкновенно заранее известно, что экстремум существует и каков его характер. Так, например, если на нашу задачу посмотреть с геометрической точки зрения (см. рис. 39.3), то мы находим на эллипсе
5x2 6xy 5y2 32 0
точки, наиболее удалённые от начала координат и наиболее близкие к нему, т.к. функция
|
|
|
f (x, y) x2 y2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
это квадрат искомого расстояния. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, что в точках |
|
|
|
|
A ( 2 2; 2 |
2 ) |
|
и |
B ( 2 2; 2 2 ) |
|||||||||||||||
достигается максимум fmax OA OB 4 , и отрезок |
AB 8 |
это большая |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ось эллипса. В точках C ( 2; |
|
2 ) и D ( 2; |
2 ) |
расстояние от начала |
||||||||||||||||||||
координат до точек эллипса минимально fmin OC OD 2 , |
и отрезок |
|||||||||||||||||||||||
CD 4 является малой осью эллипса. Более того, |
мы знаем направление |
|||||||||||||||||||||||
осей эллипса. Большая ось эллипса образует угол 450 |
с осью абсцисс. |
|||||||||||||||||||||||
Таким образом, в системе координат |
x1Oy1 уравнение эллипса имеет вид |
|||||||||||||||||||||||
|
|
|
|
x2 |
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
1 |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
16 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
284
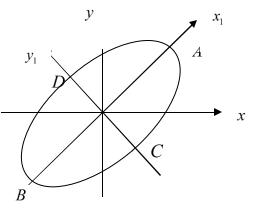
Решая задачу на условный экстремум, мы «попутно» привели уравнение эллипса 5x2 6xy 5y2 32 0 к каноническому виду.
Рис. 39.3
285

Важдаев Виктор Петрович
Коган Марк Михайлович
Лиогонький Марк Израилевич
Протасова Людмила Анатольевна
64 лекции по математике
Часть 1 (лекции 1–39)
Учебно-методическое пособие
по подготовке к лекционным занятиям по дисциплине
«Математика» для обучающихся по направлению подготовки
27.03.01 Стандартизация и метрология Направленность (профиль) Стандартизация и сертификация
Федеральное государственное бюджетное образовательное учреждение высшего образования «Нижегородский государственный архитектурно-строительный университет»
603950, Нижний Новгород, ул. Ильинская, 65. http://www. nngasu.ru, srec@nngasu.ru
