
9869
.pdf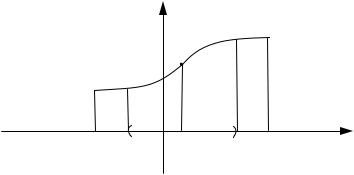
y
|
a x |
0 |
x |
0 |
x |
b |
x |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
Рис. 64 |
|
|
|
Необходимое условие перегиба функции |
y f x в точке x0 : если |
||||||
x0 – точка перегиба функции |
|
y f x и |
функция y f x имеет в |
||||
некоторой |
– окрестности точки x0 |
вторую производную, непрерывную |
|||||
в точке x0 , то |
f x0 0 . |
|
|
|
|
|
|
Достаточное условие перегиба функции y f x в точке x0 : если |
|||||||
функция y f x непрерывна в – окрестности точки x0 , имеет в точке |
|||||||
x0 конечную или бесконечную определенного знака производную f x0 , |
|||||||
а функция f |
|
|
– |
окрестности точки x0 , кроме быть |
|||
x определена в |
|||||||
может самой точки x0 , и меняет знак при переходе через эту точку, то x0 –
точка перегиба функции y f x .
Пример. Найти интервалы выпуклости (вогнутости) и точки перегиба функции y x3 3x 1.
Решение. Область определения D данной функции есть множество всех действительных чисел R , то есть D R .
Находим:
y x3 3x 1 3x2 3 ; y y 3x2 3 6x .
Используя необходимое условие перегиба, находим:
y 0 6x 0, откуда x 0 – точка «подозрительная» на точку
перегиба.
Используем достаточные условия перегиба:
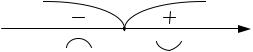
Отметим точку x 0 на области D и определим знаки y слева и справа от точки x 0.
71
y |
|
|
|
|
|
|
y |
|
0 |
x |
|
|
|
Так как x 0 D и при переходе через эту точку y меняет знак, то |
||||||
x 0 – точка перегиба данной функции. |
|
|
|
;0 |
||
Так как для любого |
x 0 |
|
то |
в |
интервале |
|
y x 0 , |
||||||
функция y выпукла вниз. |
|
|
|
|
|
0; |
Так как для любого |
x 0 |
|
то |
в |
интервале |
|
y x 0, |
||||||
функция y выпукла вверх.
Основные требования к результатам исследования и построения графика:
1) все результаты исследования функции следует обосновать в ходе решения. Все исследования функции, включая все необходимые вычисления: вычисление пределов функции, вычисление производных в точках, решение уравнений, являются необходимой частью решения задачи на построение графика функции или кривой;
2) все результаты должны быть получены точно. Необходимые приближенные вычисления привести в решении задачи;
3) масштаб построения графика следует выбирать так, чтобы были отражены основные характерные моменты поведения графика функции;
4) на рисунке изобразить пунктирной прямой вертикальные, наклонные или горизонтальные асимптоты, указать уравнения асимптот;
5) обозначить точки минимума и максимума функции, указать их координаты;
6) обозначить точки перегиба графика функции, указать их координаты;
7) обозначить координаты точек пересечения кривой с координатными осями.
y x 3 2
Пример. Построить график функции . x 1 3
Решение.
1. Областью определения D данной функции y является множество всех действительных чисел R , кроме x 1, то есть D R \ 1 .
2. Поскольку y x |
x 3 2 |
|
x 3 2 |
и y x y x и |
x 1 3 |
|
|||
x 1 3 |
||||
y x y x , то функция |
y не является четной и нечетной, то есть |
|||
данная функция y общего вида.
72
3. Находим асимптоты кривой. |
|
|
|
|
|||
Поскольку lim |
x 3 2 |
|
1 3 2 |
|
4 |
, то |
x 1 – уравнение |
x 1 |
1 1 |
0 |
|||||
x 1 |
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
вертикальной асимптоты графика данной функции y .
Наклонные асимптоты находим в виде уравнения прямой y kx b :
|
|
|
|
|
y x |
|
|
|
|
x 3 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
k lim |
|
|
lim |
|
|
|
|
|
|
|
lim |
|
|
|
x 3 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
x x 1 |
|
|
|
x x 1 3 |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
lim |
|
|
|
|
|
|
2 x 3 1 |
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
2x 6 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
x 3 3 x 3 x 1 2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 3x |
|||||||||||||||||||||||||||||||||||||
x |
|
|
x x 1 2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2x 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
lim |
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
2x 6 |
|
|
|
|
|
||||||||||||||||||||||||||||
x 1 |
4x |
1 |
|
|
x 1 2 4x 1 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
x |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
lim |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
0 |
; |
|
|
|
|||||||||
2 x 1 4x 1 x 1 2 4 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
y x kx lim |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||
b lim |
|
x |
|
|
3 |
|
0 x |
|
lim |
|
|
|
|
|
3 |
|
|
|||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x 1 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
2 x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
lim |
3 2 |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
x 1 3 |
3 x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
lim |
|
x 3 |
|
|
|
2 |
lim |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
1 |
|
|
2 |
|
0 0. |
|
|
|
|||||||||||||||||||||
|
|
x 1 2 |
|
|
2 x 1 |
|
|
|
|
3 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
3 |
x |
|
3 |
|
x |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Следовательно |
|
y 0 – |
|
|
уравнение |
|
горизонтальной |
асимптоты |
|
графика |
||||||||||||||||||||||||||||||||||||||||||
данной функции y .
4. Находим интервалы монотонности и точки экстремума функции.
|
2 |
|
2 |
|
3 |
2 |
3 |
|
|
|
|
||||||||
y |
x 3 |
|
x 3 |
|
x 1 x 3 |
x 1 |
|
|
|
|
3 |
|
|
|
3 |
2 |
|
|
|
|
x 1 |
|
|
|
x 1 |
|
|
|
|
|
2 x 3 x 1 3 x 3 2 3 x 1 2 |
|
|
||
x 1 6 |
|
|
|||
|
|
|
|
|
|
|
2x2 8x 6 3x2 18x 27 |
x2 10x 21 |
|
||
|
|
x 1 4 |
|
x 1 4 |
|
|
|
73 |
|
|
|

|
x 3 x 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
x 1 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Используя необходимое условие экстремума, находим |
y 0 |
|
|||||||||||||||||||||||
x 3 x 7 0, |
откуда |
|
x1 3 |
или x2 7 ; |
y не существует |
|
|||||||||||||||||||
x 1 4 |
0, откуда x3 |
1. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
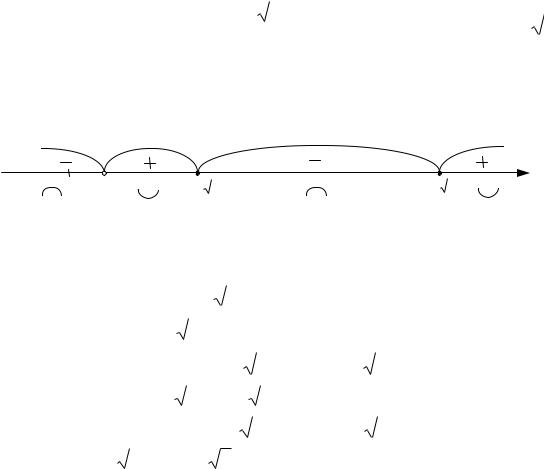
Используем достаточные условия экстремума. Найденные три |
|||||||||||||||||||||||||
критические точки наносим на область определения D и определяем знак |
|||||||||||||||||||||||||
y в каждом из четырех интервалов. |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
0 |
|
1 |
|
|
|
3 |
|
|
|
|
|
7 |
x |
|
|
|||||
|
|
|
|
0 3 0 7 |
21 |
|
|
|
|
|
|
|
|||||||||||||
y 0 |
|
|
|
0 1 4 |
|
|
|
|
|
|
21 0 |
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||
Так как |
x1 |
3 D |
и при переходе через эту точку |
y меняет знак |
|||||||||||||||||||||
минус |
на |
плюс, |
то |
x1 |
3 |
– |
точка |
минимума |
функции |
y , |
|||||||||||||||
y 3 |
3 3 2 |
|
|
0 |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 1 3 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Так как |
x2 |
7 D и при переходе через эту точку |
y |
меняет знак |
|||||||||||||||||||||
плюс |
на |
минус, |
то |
x2 |
7 |
– |
точка |
максимума |
функции |
y , |
|||||||||||||||
y 7 |
7 3 2 |
|
16 |
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
7 1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
216 |
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Так |
как |
при |
x 1, |
|
1 x 3, |
x 7 |
|
|
в |
интервалах |
|||||||||||||||
|
y x 0 , то |
||||||||||||||||||||||||
;1 , 1;3 , |
7; функция y монотонно убывает. |
|
|
|
|||||||||||||||||||||
Так как при 3 x |
7 |
|
|
|
|
|
|
|
|
функция y |
|||||||||||||||
y x 0, то в интервале 3;7 |
|||||||||||||||||||||||||
монотонно возрастает.
5. Находим интервалы выпуклости (вогнутости) кривой и точки
перегиба. |
|
|
|
|
|
|
|
|
|
|
|
|
x 3 x 7 |
|
|
||
|
|
|
|
|
||||
y y |
|
|
4 |
|
|
|
||
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
|
x 3 x 7 x |
1 |
x 3 x 7 x 1 |
|
|
|||
|
|
|
|
x 1 4 2 |
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
74 |
|
|
|
x 7 x 3 x 1 4 x 3 x 7 4 x 1 3 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2x 10 x 1 4 x2 10x 21 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x 1 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2x2 12x 10 4x2 40x 84 |
|
2x2 28x 74 |
. |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
x 1 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 5 |
|
|
|
|
|
|
|
||||||||||||||||
Итак, |
|
y |
2 x2 14x 37 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
x 1 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Используя |
необходимое условие перегиба, |
|
находим |
y 0 |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
x2 14x 37 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
196 148 |
|
|
|
|
|
|
|
|
7 2 |
|
|
|||||||||||||||||||||
или x |
|
|
|
|
|
|
|
|
|
, откуда |
x |
3 ; |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
1, 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1,2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y не существует x 1 5 0 , откуда x3 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Используем достаточные условия перегиба. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||||||||||||
y |
0 |
|
1 |
|
|
7 2 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 2 3 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74 |
74 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y 0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Так как точки x1,2 7 2 |
3 |
D и при переходе через эти точки |
y |
||||||||||||||||||||||||||||||||||||||||||
меняет знак, то x1,2 7 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
3 – точки перегиба графика функции y . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так |
как при |
|
x 1, |
|
|
|
7 2 |
|
3 x 7 2 |
3 |
|
|
то |
|
в |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
y |
x 0 , |
|
|||||||||||||||||||||||||||||||||||||
интервалах ;1 , |
7 2 |
|
|
|
|
|
|
|
|
|
|
|
|
функция y выпукла вниз. |
|
|
|
||||||||||||||||||||||||||||
3;7 2 |
|
3 |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так |
как при |
|
1 x 7 2 |
3 , |
|
|
x 7 2 |
3 |
|
то |
в |
||||||||||||||||||||||||||||||||||
|
|
|
y |
x 0, |
|||||||||||||||||||||||||||||||||||||||||
|
1;7 2 |
|
|
, 7 2 |
3; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
интервалах |
|
3 |
функция y выпукла вверх. |
|
|
|
|||||||||||||||||||||||||||||||||||||||
6. Находим координаты точек пересечения кривой с координатными |
|||||||||||||||||||||||||||||||||||||||||||||
осями: |
|
|
|
|
|
|
x 3 2 0, откуда x 3; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Ox : |
y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 3 2 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Oy : x 0 y 0 1 3 |
|
|
9 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
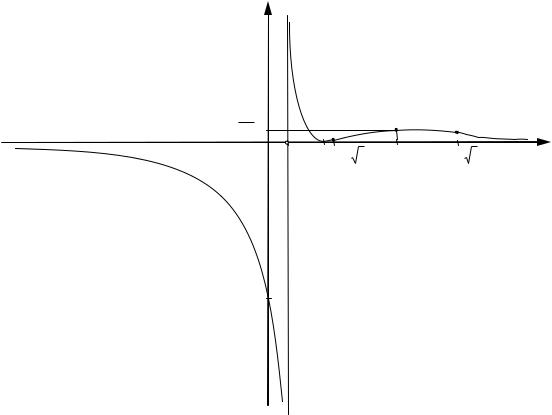
7. Строим эскиз графика данной функции. (См. рис. 65).
75
y
|
2 |
|
|
y 0 |
27 |
|
|
|
0 1 3 7 2 3 7 |
7 2 3 |
x |
-9
x 1 |
Рис. 65 |
|
76
Контрольные задания
|
|
|
|
|
Задание 1 |
||
Найти матрицу C AT B , если: |
|
||||||
|
2 |
3 |
|
1 |
0 |
||
1.01. A |
|
|
|
, B |
|
|
. |
|
4 |
5 |
|
|
2 |
|
|
|
|
|
3 |
||||
|
0 |
2 |
|
|
4 |
1 |
|
1.02. A |
|
|
|
, B |
|
|
. |
|
3 |
1 |
|
|
0 |
6 |
|
|
|
|
|
||||
|
3 |
2 |
|
|
4 |
3 |
|
1.03. A |
|
|
|
, B |
|
|
. |
|
0 |
4 |
|
|
2 |
|
|
|
|
|
1 |
||||
3 |
0 |
|
|
2 |
1 |
|
|
1.04. A |
|
|
|
, B |
|
|
. |
|
2 |
1 |
|
|
0 |
|
|
|
|
|
3 |
||||
|
|
4 |
1 |
|
|
0 |
1 |
|
|
||||
1.05. |
A |
|
, |
B |
|
|
|
. |
|
|
|||
|
|
0 |
|
|
|
1 |
6 |
|
|
|
|||
|
|
5 |
|
|
|
|
|
||||||
|
|
2 |
0 |
|
|
2 |
1 |
|
|
|
|||
1.06. |
A |
|
|
|
, B |
|
|
|
. |
|
|||
|
|
0 |
4 |
|
|
|
0 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1.07. |
|
0 |
2 |
|
|
|
1 |
|
2 |
|
|
||
A |
|
|
|
, B |
|
|
|
|
. |
||||
|
|
1 |
3 |
|
|
|
1 |
|
2 |
|
|
||
|
|
|
|
|
|
|
|||||||
1.08. |
|
3 |
4 |
|
|
|
0 |
|
6 |
|
|
||
A |
|
|
|
, B |
|
|
|
|
. |
||||
|
|
5 |
1 |
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
3 |
|
|||||||
|
2 |
0 |
|
|
4 |
0 |
|
|
|
||||
1.09. |
A |
|
|
|
, B |
|
|
|
. |
|
|||
|
|
3 |
1 |
|
|
|
1 |
6 |
|
|
|
||
|
|
|
|
|
|
|
|
||||||
|
4 |
1 |
|
2 |
|
1 |
|||||||
1.10. |
A |
|
|
|
|
, B |
|
|
|
|
. |
||
|
|
0 |
5 |
|
|
|
0 |
|
1 |
|
|||
|
|
|
|
|
|
|
|||||||
77
Задание 2
Решить систему по правилу Крамера.
3x1 x2 3x3 6 |
||||
|
x1 x2 |
x3 |
0 . |
|
2.01. |
||||
|
|
3x2 |
4x3 2 |
|
2x1 |
||||
4x1 x2 x3 3 |
||||
|
x1 |
x2 5x3 |
2 . |
|
2.02. |
||||
|
|
3x2 |
x3 |
1 |
2x1 |
||||
x1 x2 5x3 5
2.03. 2x1 3x2 2x3 3.
x1 2x2 3x3 0
x1 3x2 x3 2 |
||||
|
2x1 x2 2x3 0 . |
|||
2.04. |
||||
3x x |
2 |
5x 2 |
||
|
1 |
|
3 |
|
|
x1 x2 4x3 2 |
|||
|
|
2x2 x3 3. |
||
2.05. x1 |
||||
|
x1 3x2 x3 4 |
|||
|
||||
|
3x1 x2 x3 0 |
|||||||
|
x1 x2 |
|
3x3 |
4 . |
||||
2.06. |
|
|||||||
|
|
|
|
|
|
|
|
|
2x1 x2 3x3 4 |
||||||||
|
x1 x2 x3 1 |
|||||||
|
|
|
|
|
|
|
3x3 2 . |
|
2.07. 2x1 x2 |
||||||||
|
2x1 x2 2x3 1 |
|||||||
|
||||||||
x |
4x |
|
|
|
x |
0 |
||
|
1 |
|
2 |
|
|
3 |
|
|
2.08. 2x1 x2 |
|
2x3 |
0 . |
|||||
|
|
|
|
|
|
|
|
4 |
2x1 2x2 x3 |
||||||||
4x1 x2 x3 3 |
||||||||
|
|
2x2 |
|
x3 1. |
||||
2.09. x1 |
|
|||||||
|
|
|
|
|
|
|
|
0 |
x1 x2 3x3 |
||||||||
x1 x2 x3 0 |
||||||||
|
2x1 x2 x3 |
1 . |
||||||
2.10. |
||||||||
3x 3x |
2 |
2x 5 |
||||||
|
1 |
|
|
|
3 |
|||
78
Задание 3
Дана пирамида ABCD . Найти:
1)угол ABC грани ABC ;
2)площадь грани BCD ;
3)объем пирамиды ABCD , если
3.01. A 1; 2;3 , B 0; 1;1 , C 1;0; 2 , D 2;3;0 . 3.02. A 4;3;1 , B 0; 2;3 , C 3;0; 3 , D 1;1;0 . 3.03. A 2;3; 4 , B 0; 1;1 , C 3;0; 2 , D 2;3;0 . 3.04. A 3; 4;1 , B 0; 1;3 , C 2;0; 1 , D 1; 2;0 . 3.05. A 4;5; 2 , B 0; 2;1 , C 1;0; 3 , D 2; 2;0 . 3.06. A 3; 2;1 , B 0;1; 2 , C 2;0; 1 , D 3;3;0 . 3.07. A 1;3;5 , B 0; 2; 1 , C 2;0;3 , D 2; 1;0 . 3.08. A 1; 4;6 , B 0;1; 1 , C 2;0; 2 , D 1; 2;0 .
3.09.A 2; 4;1 , B 0; 1; 2 , C 1;0; 2 , D 2;1;0 .
3.10.A 3;1; 2 , B 0; 1; 3 , C 1;0;1 , D 1;3;0 .
78
Задание 4
Дан ABC . Найти:
1)уравнения его сторон;
2)уравнение высоты, опущенной из вершины A на сторону BC ;
3)уравнение медианы AM ;
4)уравнение прямой, проходящей через точку A и параллельной
медиане AM , если |
|
4.01. A 0; 2 , |
B 1;0 , C 2;1 . |
4.02. A 0; 1 , B 2;0 , C 3; 4 . |
|
4.03. A 0;1 , |
B 1;0 , C 4;3 . |
4.04. A 0;3 , |
B 1;0 , C 2;1 . |
4.05. A 0; 2 , B 1;0 , C 3; 4 . |
|
4.06. A 0; 4 , |
B 4;0 , C 2; 3 . |
4.07. A 0;3 , |
B 3;0 , C 2; 3 . |
4.08. A 0;1 , |
B 3;0 , C 2; 3 . |
4.09.A 0; 1 , B 3;0 , C 4; 2 .
4.10.A 0; 2 , B 2;0 , C 1;1 .
79
