9703
.pdf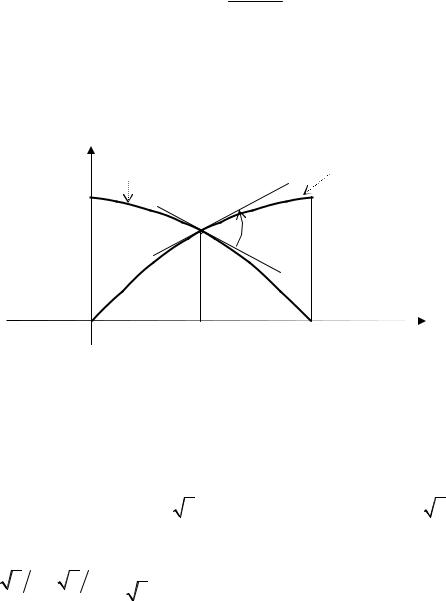
[Введите текст]
y − y0 = f ′(x0 )(x − x0 ) ,
а уравнение нормали
y − y0 = − |
|
|
1 |
(x − x0 ) . |
f |
′ |
|
||
|
|
(x0 ) |
||
Под углом между кривыми в точке их пересечения естественно понимать наименьший из углов между касательными к кривым в этой точке. Тогда угол может быть вычислен как угол между двумя прямыми с заданными угловыми коэффициентами по формуле
tgϕ = k2 − k1 . 1 + k1k2
Вкачестве примера найдем, под каким углом пересекаются синусоида
икосинусоида. Задача сводится к нахождению значений производных
функций f1 (x) = cos x и f2 (x) = sin x |
при x = π / 4 (см. рис. 18.3). |
|
y |
= cos x |
y2 = sin x |
y1 |
||
1 |
|
|
|
|
ϕ ≈ 700 |
x
π |
π |
4 |
2 |
Рис. 18.3
Вычисляем угловые коэффициенты касательных к заданным кривым в точке их пересечения
k |
= f ′(x) | |
x=π / 4 |
= −sin( π) = − |
|
2 |
|
, |
k |
|
= f ′(x) | |
x=π / 4 |
= cos( π) = |
|
2 |
|
. |
|
|
|
2 |
|
||||||||||||
1 |
1 |
4 |
2 |
|
|
|
2 |
4 |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Отсюда
tgϕ = |
|
2 |
2 + |
2 |
2 |
= 2 |
|
ϕ ≈ 700 . |
|
2 |
|||||||
|
|
|
|
|
||||
|
|
|
1 − 0.5 |
|||||
18.4. Правила дифференцирования. Непосредственное нахождение производных некоторых функций представляет собой трудоемкую задачу.
130
[Введите текст]
Поэтому выведем правила дифференцирования, которые значительно упростят ее.
Производная суммы конечного числа дифференцируемых функций равна сумме производных этих функций
(u(x) + v(x))′ = u′(x) + v′(x) .
Действительно, приращение суммы равно
y = u( x + x) + v( x + x) − u( x) − v( x) = u( x + x) − u( x) + v( x + x) − v( x) ,
т.е. y = u + v .Следовательно,
y¢ = lim |
Dy |
= lim |
Du + |
Dv |
= lim |
Du |
+ lim |
Dv = u¢ + v¢, |
x→0 |
Dx |
x→0 |
Dx |
Dx |
x→0 |
Dx |
x→0 |
Dx |
так как предел суммы равен сумме пределов и последние пределы существуют в силу предположения о дифференцируемости слагаемых.
Производная произведения двух дифференцируемых функций равна сумме произведений каждой функции на производную другой функции
′ |
|
′ |
|
′ |
|
(18.1) |
(u(x)v(x)) |
= u(x)v (x) + v(x)u (x) . |
|
||||
Действительно, дадим приращение аргументу |
x . Тогда сомножите- |
|||||
ли получат приращения |
|
u и v |
соответственнои приращение функции |
|||
равно |
|
|
|
|
|
|
D y = (u + Du )(v + Dv) - uv = u × Dv + v ×Du + Du × Dv . |
||||||
Следовательно, |
|
|
|
|
|
|
′ |
y |
= v lim |
u |
v |
+ lim |
u |
y = lim |
|
x |
+ u lim |
lim v . |
||
x→0 x |
x→0 |
x→0 x |
x→0 |
x x→0 |
||
Так как функция v( x) |
– дифференцируемая, то она непрерывная, по- |
|||||
этому последнее слагаемое в этой формуле равняется нулю и мы приходим к формуле (18.1).
В качестве следствия получим следующее правило: постоянный
множитель при дифференцировании выносится за знак производной
(cf (x))′ = cf ′(x) .
131
[Введите текст]
Применим это правило для нахождения, производной0, , [ 1 логарифмической функции с произвольным основанием
(loga |
x)¢ = |
|
|
= |
1 |
(ln x)¢ = |
1 |
× |
. |
|
|
ln x ¢ |
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
ln a |
|
ln a |
|
ln a |
|
x |
|||
Производная частноговычисляется по следующей формуле:
u ¢ |
= |
u¢v - v¢u |
|||
|
|
|
|
|
|
|
v |
2 |
|||
v |
|
|
|||
при условии, что знаменатель в данной точке не обращается в ноль. Действительно, выразим приращение частного через приращения делимого и делителя
|
|
|
|
y = |
u + |
u |
− |
u |
= |
v |
u − u v |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
v + v |
v |
v (v + v) |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
y |
|
v lim |
u − u lim |
v |
′ |
|
|
′ |
|
|
|
|
|
|
|
|||||||||
Тогда |
lim |
= |
x→0 |
x |
|
|
|
x→0 |
x |
= |
|
u v − v u |
. |
|
|
|
|
|
|
|
|||||||
x |
|
lim v |
(v + |
v) |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x→0 |
|
|
|
|
|
|
v2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдём, например, производную функции y = tg x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
sin x ¢ |
(sin x)¢cos x - (cos x)¢sin x |
|
sin2 |
x + cos2 x |
|
1 |
|
|
|||||||||||||||||||
(tg x)¢ = |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
= |
|
|
|
. |
|
|
|
|
cos |
2 |
(x) |
|
|
|
|
|
|
|
cos |
2 |
x |
cos |
2 |
|
||||||||
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||||
Получите самостоятельно производную функции |
y = ctg x . |
|
|
|
|
|
|
||||||||||||||||||||
Лекция 19. Производная (продолжение)
132
[Введите текст]
19.1. Дифференцирование сложной и обратной функций.Часто приходится находить производную так называемой сложной функции, представляющей собой «функцию от функции». Например,
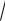x2 +1, sin(2x + 3), e− x2
или в общем виде
y = f (ϕ( x)) = F ( x) .
Эта функция представлена как суперпозиция (композиция)двух функций
|
y = f (u), |
u = u( x) , |
|
где «внешняя» функция |
f (u) – дифференцируемая функция промежуточ- |
||
ной переменной u , а «внутренняя» функция u ( x) – |
дифференцируемая |
||
функция независимой |
переменной |
x . Оказывается, |
что производная |
сложной функции по независимой переменной равна произведению производной функции по промежуточнойпеременной на производную промежуточнойпеременной по независимой переменной
y′ = f ′(u(x))u′(x) .
x u
Это так называемое цепное правило доказывается следующим образом. Используя определение производной, получим
y¢ |
= lim |
y = lim |
y × lim |
u . |
|
x |
x→0 D x |
x→0 Du x→0 D x |
|||
|
|||||
В силу непрерывности функции |
u ( x) из условия |
x → 0 следует, что |
|||
u → 0 . Отсюда вытекает указанная формула в предположении, что |
|||||
Du ¹ 0. |
u = u(x + |
x) −u(x) = 0, т.е. u(x + x) = u(x) то |
|||
Если же окажется, что |
|||||
y = f (u(x + x)) − f (u(x)) = 0 . Значит, |
′ |
′ |
|
||
u (x) = 0и y (x) = 0и формула диф- |
|||||
ференцирования сложной функции |
0 = fu′(u(x)) ×0 справедлива и в этом |
||||
случае.Далее, многие элементарные функции определены как обратные |
|||||
функции к другим функциям, например, y = arcsin x , |
y = ln x . |
||||
Возникает вопрос: нельзя ли найти производную обратной функции, зная производную исходной функции?Оказывается, можно. А именно, если
для функции y = f ( x) (например, для y = arcsin x ) существует обратная функция x = ϕ( y) ( x = sin y , −π / 2 ≤ y ≤ π / 2 ), которая в рассматриваемой
133
[Введите текст]
точке y имеет производную j′( y) ¹ 0 ветствующей точке x функция y = мую по правилу
f ¢(x) = |
1 |
, |
|
j¢( y) |
|||
|
|
(в нашем примере, cos y ), то в соот- f ( x) имеет производную, вычисляе-
(19.1)
в котором y = f ( x) . В нашем примере
′ |
= |
1 |
= |
1 |
= |
|
|
1 |
|
|
|
= |
1 |
|
|
, |
|
(arcsin x) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
′ |
|
|
|
|
|
|
|
|
|
|
|
||||||
cos y |
|
− sin |
2 |
|
1 − x |
2 |
|||||||||||
|
|
(sin y) |
|
+ 1 |
|
y |
|
|
|
||||||||
где знак « + » взят в силу того, что в промежутке -p / 2 £ y £ p / 2 , в котором обратная функция существует, cos y положителен.
Для доказательства формулы (19.1) продифференцируем равенство
x = j( y) по переменной x , |
применяя правило дифференцирования слож- |
|||
ной функции (считая y функцией x ): |
|
|
|
|
|
1 = x'y × yx' |
, |
||
откуда следует |
|
|
|
|
|
y¢ = |
1 |
. |
|
|
|
|
||
|
x |
x¢y |
|
|
|
|
|
|
|
Геометрический смысл этой формулы виден из рис. 19.1 |
||||
|
y |
|
|
x = j( y) |
|
y |
β |
y = f ( x) |
|
|
|
|||
|
α |
|
|
x |
|
|
|
|
x |
|
Рис. 19.1 |
|
||
Касательная к кривой |
y = f ( x) образует с положительным направле- |
|||
нием оси |
Ox угол α . Касательная к той же кривой x = j( y) образует |
угол β с |
положительным направлением оси Oy . Согласно геометриче- |
скому смыслу производной f |
′ |
′ |
α и β до- |
(x) = tgα |
и ϕ ( y) = tgβ. Но углы |
полняют друг друга доπ / 2 , поэтому tga × tgb = 1 . Это соотношение и выражает формулу дифференцирования обратной функции.
134
[Введите текст]
Найдём производную показательной функции y = a x , a > 0 . Обрат-
ная для неё функция |
|
x = loga |
y . Применяя формулу (19.1)имеем |
|
|||||||||||||
|
|
x |
′ |
= |
1 |
|
= |
|
1 |
|
|
|
= y ln a = a |
x |
|
|
|
|
(a |
) |
|
|
|
|
|
ln a |
|
||||||||
|
|
′ |
|
1 1 |
|
|
|||||||||||
|
|
|
|
|
(loga y) |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ln a y |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Применяя это правило, найдите самостоятельно производные функций |
|||||||||||||||||
|
|
|
|
|
|
arccos x , arctgx . |
|
|
|
|
|||||||
Применим |
формулу |
производной |
показательной |
функции |
|||||||||||||
(a x )′ = a x ln a для вывода производной степенной функции |
|
||||||||||||||||
(xα )′ = (eα ln x )′ = eα ln xα 1 = αxα−1 . x
19.2.Дифференцированиефункций, заданных параметрически. Касательная к параметрически заданной кривой. Получим теперь правило нахождения производной параметрически заданной функции. Такая функция, например, возникает в задаче о траектории фиксированной точки M окружности радиуса r , катящейся без скольжения по оси Ox .
M |
C |
r |
|
t K |
|
O N |
P |
OP = MP = r t |
|
x = OP − NP = r t − r sin t |
|
y = r − KC = r − r cos t |
x |
|
2π r |
Рис. 19.2
135
[Введите текст]
Пусть в начальный момент точка M находится в начале координат. В качестве параметра возьмем угол t , на который повернется радиус окружности O1O , приняв положение CM . Выразим координаты точки M ( x, y) как функции параметра t . Из рисунка видно, что длина дуги MP равна длине отрезка OP и равна rt . Следовательно, из треугольника MKC найдём
x = r(t − sin t) |
≤ t ≤ 2π . |
|
|
0 |
|
y = r(1 |
− cos t) |
|
Выбранные границы изменения параметра соответствуют одному обороту окружности. Таким образом, мы получили зависимость переменной y от переменной x , выраженную не явно, а через промежуточный параметр t . График этой зависимости представлен на рис. 19.2, а кривая называется циклоидой. Название циклоида означает: «напоминающая о круге». Его дал Галилео Галилей (1564–1642). Конечно, можно связать x и y непосредственно, исключив параметр t . Однако эта функция будет иметь достаточно сложный вид, поэтому возникает необходимость в нахождении производной y как функции переменной x на основе параметрического задания функции.
Рассмотрим задачу в общем виде. Пусть функция y = f ( x) задана параметрически
x = ϕ (t) |
, |
|
α ≤ t ≤ β , |
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
y =ψ (t) |
|
|
|
|
|
|
|
|
|
|
где функции ϕ(t ) и ψ (t ) – |
дифференцируемы и функция ϕ(t ) имеет об- |
|||||||||
ратную. Тогда по определению производной имеем |
||||||||||
|
|
|
lim |
y |
|
lim |
y |
|
′ |
|
′ |
y |
|
t |
|
t |
|
|
|||
|
x→0 |
|
t→0 |
|
ψt |
|
||||
yx = lim |
|
= |
|
|
= |
|
|
= |
′ |
. |
|
|
x |
|
x |
||||||
x→0 |
|
|
|
|
|
|
|
|||
x |
|
lim |
|
|
lim |
|
|
ϕt |
|
|
|
|
|
x→0 |
t |
|
t→0 |
t |
|
|
|
Здесь мы использовали то, что в силу непрерывности обратной функции к из x → 0 следует
Задача. Получить уравнение касательной к циклоиде.Пусть окружность радиуса r = 1 совершила одну шестую часть оборота. Найдем уравнение касательной в соответствующей точке траектории. Одна шестая часть оборота окружности соответствует значению параметра t0 = π / 3 , а координаты точки:
136
[Введите текст] |
|
|
|
|
|
|
|
|
|
|
|
|
x0 = x(t0 ) = (t − sin t) t =π / 3 |
= π / 3 − |
3 / 2 , |
y0 = y(t0 ) = 1 − cost t=π / 3 = 0,5 . |
|||||||||
Производную |
′ |
|
|
|
|
|
|
|
|
|
|
|
yx находим как производную функции заданной пара- |
||||||||||||
метрически |
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
sin t |
2sin t |
cos t |
|
|
|
t |
|
|
|
|
|
= |
2 |
2 |
= ctg |
|
|
|
|||||
|
yx = |
− cost |
|
2 t |
|
2 |
|
|
|
|||
|
1 |
|
2sin |
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
π |
|
|
|
||
|
|
|
|
′ |
|
|
|
|
|
|||
В данной точке циклоиды она равна |
|
|
|
= ctg |
= |
3 . Поэтому |
||||||
yx = ctg |
|
2 |
||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
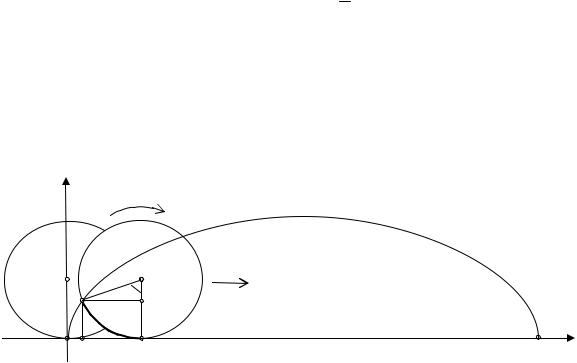
уравнение касательной в этой точке y = |
3x + 2 − π / |
3 (см. рис. 19.2). |
||||||||||
2.5 |
y=sqrt3*x+2-pi/sqrt3 |
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
x = t - sint |
|
|
|
|||
|
|
|
|
|
|
y =1 - cost |
|
|
|
|||
0.5 |
|
|
|
|
|
0 < t < pi |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X: 0.18 |
|
|
|
|
|
|
|
|
|
|
|
|
Y: 0.498 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
-0.5 |
0 |
0.5 |
1 |
1.5 |
|
2 |
|
2.5 |
|
3 |
3.5 |
|
-0.5 |
|
|
|
|||||||||
Рис. 19.3
19.3. Производная функции, заданной неявно. Касательная к неявно заданной кривой.Рассмотрим случай, когда функция задана неяв-
но. Пример такой функции y = f ( x) дается уравнением
x2 |
+ |
y2 |
= 1 ( y > 0 ). |
|
a2 |
b2 |
|||
|
|
Графиком этой функции служит верхняя половина эллипса. Покажем, как находить производную этой функции, не выражая явно y через x (для некоторых неявно заданных функций такое вообще невозможно). Продиффе-
137
[Введите текст] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ренцируем это уравнением по переменной |
x , считая, |
что переменная y |
||||||||||||||||||||||
является функцией x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
′ |
|
|
|
|
|
|
|
|
b2 x |
|
|
|
|
|
|
|
a2 |
2x + b2 |
2yy |
|
= 0 |
] y′ = − a2 y |
|
|
|||||||||||||
|
В общем случае неявно заданной функции нужно действовать анало- |
|||||||||||||||||||||||
гичным образом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача.Получить уравнение касательной к |
|
эллипсу в точке M 0 ( x0 , y0 ) . |
||||||||||||||||||||||
Уравнение касательной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
y − y |
|
= − b2 x0 ( x − x |
|
) |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
a 2 y |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
после умножения на |
y0 |
|
|
примет вид |
x0 |
x + y0 |
y = 1. |
|
||||||||||||||||
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
|
a2 |
|
b2 |
|
|
|
|
|
|
||
|
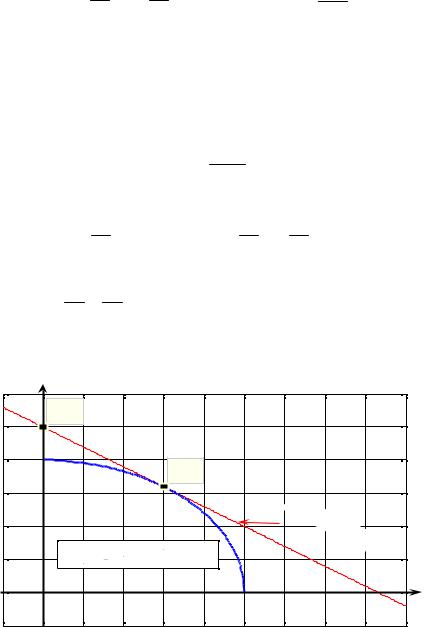
Для эллипса |
|
x2 |
+ y2 |
= 1 |
в точке |
M |
0 |
(3, 1.6) |
|
уравнение касатель- |
|||||||||||||
|
|
|
25 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ной |
3x + 10 y − 25 = 0 |
(см. рис. 19.4). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X: 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y: 2.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
X: 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Y: 1.6 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
5= |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||
|
0.5 |
|
1/25x |
|
+ 1/4y |
|
|
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.5 |
0 |
1 |
|
|
|
2 |
3 |
|
|
|
4 |
5 |
|
6 |
|
|
|
|
7 |
8 |
9 |
||
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 19.4 |
|
|
|
|
|
|
|
|
|
|
|||
|
19.4. Логарифмическое дифференцирование.Применим метод на- |
|||||||||||||||||||||||
хождения производной неявно заданной функции к выводу производной |
||||||||||||||||||||||||
показательно-степенной функции вида |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
y = u(x)v( x) .
Прологарифмируем обе части этого равенства, опуская для краткости аргумент
138
[Введите текст]
ln y = v ln u .
Найдем теперь y′( x) как производную неявно заданной функции
|
|
1 |
y |
′ |
|
|
′ |
|
1 |
u |
′ |
|
|
||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
y |
|
= v ln u + v |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
и отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
v |
′ |
|
|
|
1 |
′ |
v |
|
|
|
′ |
|
v−1 ′ |
|
= u |
|
|
|
|
|
|
|
|
+ vu |
||||||
y |
(v ln u + v u ) = u |
|
ln u v |
u . |
|||||||||||
u
Этот прием, называемый логарифмическим дифференцированием,
применим также для упрощения нахождения производных. Например,
|
( x + 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y = |
|
x −1 |
, |
|
ln y = 2ln ( x + 1) + |
1 |
ln ( x −1) − 3ln ( x + 4) − x, |
||||||||||||||||||
|
( x + 4)3 ex |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
|
1 |
|
′ |
2 |
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|||||||
|
|
|
|
y |
|
= |
|
|
|
+ |
|
|
|
− |
|
|
−1, |
|
|
||||||
|
|
|
y |
|
x + 1 |
2( x −1) |
x + 4 |
|
|
||||||||||||||||
|
|
( x + 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y′ = |
|
|
x −1 |
|
2 |
|
|
1 |
|
|
|
|
3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
− |
|
|
−1 |
||
|
( x + 4)3 ex |
|
|
( x + 1) |
|
2( x −1) |
|
+ 4 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||||||
19.5. Сводка формул производных и правил дифференцирования.
Сведём в одном месте формулы производных элементарных функций
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
α ′ |
α−1 |
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
( x ) = |
|
|
|
|
|
|
||||||||||||||||||||
(x |
) = αx |
|
|
, |
|
|
|
|
|
= − |
|
|
, |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x |
2 |
2 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
x |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
(sin x)′ = cos x, |
(cos x)′ = − sin x |
|
|
|
|
|
|
|||||||||||||||||||||||
|
(tgx)′ = |
|
1 |
|
|
|
, |
(ctgx)′ = − |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
sin2 x |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
(a rc s in x )′ = |
|
|
|
|
1 |
|
|
|
, |
(arccos x)′ = − |
1 |
|
|
|
|
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 − x2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1 |
− x 2 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(arctgx )′ = |
1 |
|
|
|
|
, (arcctgx)′ = − |
|
1 |
|
, |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
+ x |
2 |
|
|
||||||||||||||||||||
1 + x 2 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
139 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||