
9698
.pdf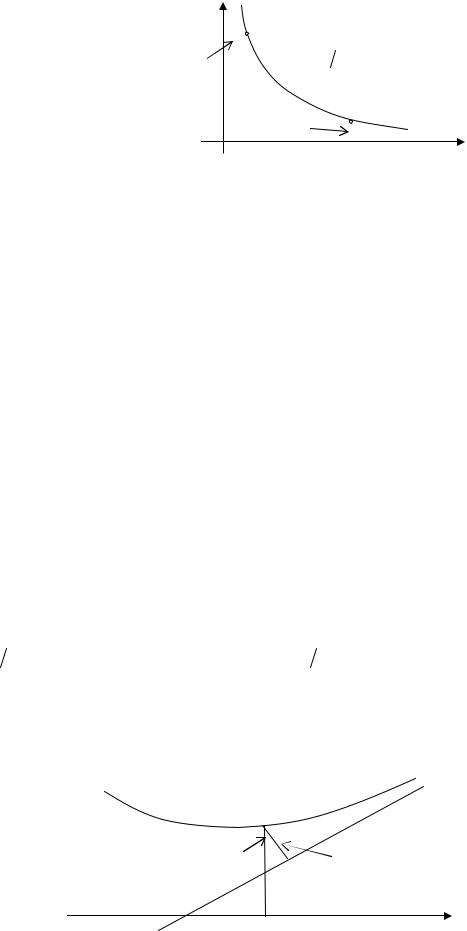
|
|
|
M (x, y) |
||
|
|
|
|
||
|
|
|
|||
d = x |
|
|
y = 1 x |
||
|
|
|
d = y |
|
N(x, y) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Рис. 23.7
Рассмотрим одну из ветвей этой кривой. Когда точка M (x, y) стремится к бесконечности, то расстояние её до оси Oy , равное d = x , стремится к нулю. Значит прямая x = 0 – вертикальная асимптота. Если N(x, y) → ∞, то d = y → 0 . Следовательно, прямая y = 0 – горизонтальная асимптота. Как найти вертикальные асимптоты кривой, заданной уравнением y = f (x)? Необходимым условием для этого является существование точек разрыва функции. Достаточным условием будет одно из следующих:
lim f (x) = ± ∞ ,
x→x0 ±0
где x0 точка разрыва.
Горизонтальные асимптоты кривых, определённых в бесконечном промежутке, определяются существованием конечных пределов:
lim |
f (x) = a , |
lim |
f (x) = b . |
|
|
x→+∞ |
x→−∞ |
|
|
||
В этом случае прямые y = a |
и |
y = b |
– |
горизонтальные асимптоты. |
|
Например, график функции |
y = arctg x |
при |
x → + ∞ |
имеет асимптоту |
|
y = π 2 , а при x → − ∞ асимптоту |
y = − π 2 |
(см. рис. 23.5). |
|||
Пусть кривая, заданная уравнением |
y = f (x) , |
имеет наклонную |
|||
асимптоту y = k x + b . Как найти |
величины |
k и |
b? Ограничимся |
||
рассмотрением случая, когда |
x → + ∞ . |
|
|
|
|
y = f (x) |
N |
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
d = MN cos α |
|
M
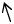 α
α
x
160

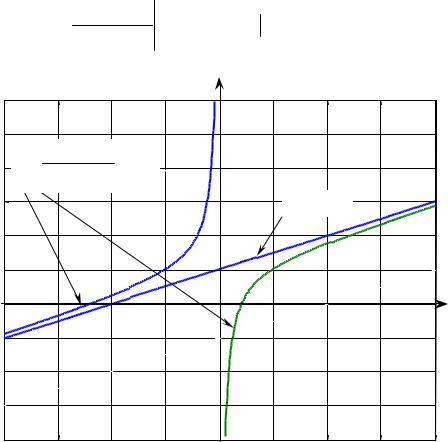
и приведем графики функции и её наклонной асимптоты |
y = x + 2 |
|
||||||
Используя свойство асимптоты, найдем |
|
|
|
|
||||
|
x |
2 + 2x − 1 |
|
≈ (x + 2) x=2016 |
= 2018. |
|
|
|
|
|
x |
|
|
|
|||
|
|
x=2016 |
|
|
|
|
||
|
|
|
|
|
|
|
||
12 |
|
|
|
|
|
|
|
|
10 |
y = x2 + 2 x − 1 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
y = x + 2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
-6 |
|
|
|
|
|
|
|
|
-8 |
|
|
|
|
|
|
|
|
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
|
|
|
Рис. 23.9 |
|
|
|
|
23.4. Примерный план исследования функции. Приведём краткий |
||||||||
перечень вопросов, на которые нужно ответить при исследовании |
||||||||
функции. |
|
|
|
|
|
|
|
|
1.Область определения. Чётность, нечётность, периодичность. Исследование в окрестности точек разрыва (возможны вертикальные асимптоты). Точки пересечения с осями, поведение на бесконечности (возможны горизонтальные асимптоты).
2.Экстремумы. Интервалы возрастания и убывания (различать «гладкие» экстремумы и «остриё» или излом).
3.Точки перегиба, интервалы выпуклости (полезно вычислить производную в точке перегиба)
4.Наклонные асимптоты.
162

Заметим, что перечисленный порядок вопросов совсем не обязательный.
Лекция 24. Кривизна. Приближённое решение уравнений
24.1. Понятие кривизны. Одна и та же кривая в разных точках искривлена по-разному. Например, синусоида в точках пересечения с осью абсцисс почти прямая, а в вершинах дуг наиболее искривлена. Более того, на различных участках она искривлена в разном направлении. Нельзя ли как-то определить кривизну в данной точке кривой? Оказывается можно. Для этого определим сначала среднюю кривизну некоторого участка кривой.
Пусть при перемещении |
точки по кривой из положения M1 в |
||
положение M 2 касательный вектор повернётся на угол Δα. Обозначим |
|||
пройденное расстояние через |
s . Ясно, что Δα есть функция s (см. рис. |
||
24.1). |
|
|
|
|
|
Δα |
|
|
M 2 |
|
|
|
s |
|
|
M1 |
α |
|
|
|
|
|
|
|
|
|
|
|
Рис. 24.1 |
||
Отношение |
Δα = k |
||
|
|||
|
s |
cp |
|
|
|
|
|
назовём средней кривизной участка кривой |
s . |
|
Рассмотрим некоторые примеры. Перемещение точки вдоль прямой |
||
на расстояние |
s не меняет направления |
касательного вектора, т.е. |
|
163 |
|
Δα = 0 . Таким образом, средняя кривизна любого участка прямой линии равна нулю, что не противоречит здравому смыслу.
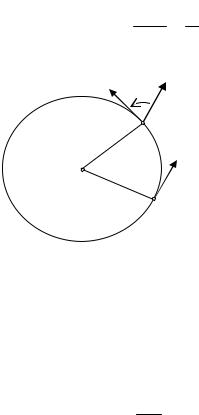
Пусть теперь точка «прошла» некоторую дугу s окружности радиуса R . Поскольку длина дуги окружности с центральным углом Δα равна
s = RΔα, то средняя кривизна любой части окружности равна
k |
|
= Δα |
= Δα |
= 1 |
|
cp |
s |
R |
s |
R |
|
|
|
||||
|
|
|
Δα |
|
|
|
|
|
|
|
s |
|
O |
Δα |
|
|
|
|
|
|
|
||
|
|
Рис. 24.2 |
|
|
|
Естественно теперь ввести понятие кривизны в данной точке как предел средней кривизны, когда длина участка s стремится к нулю
k = lim Δα = dα , s→0 s ds
т.е. кривизна равна производной угла поворота касательного вектора по длине кривой.
24.2. Вычисление кривизны плоской кривой. Для вывода формулы кривизны кривой y = f (x) продифференцируем по переменной s равенство, выражающее геометрический смысл ее производной
α(s) = arctg y′x .
Пользуясь правилом дифференцирования сложной функции, получим
dα |
|
ds |
= |
|
y |
′′ |
. |
|
|
|
1 + |
y′2 |
|||
ds dx |
|
||||||
164

|
|
|
|
|
|
|
dα |
|
|
|
y′′ |
||
|
|
′2 |
|
|
|
|
|
|
|
||||
Поскольку |
ds = 1+ y |
dx , |
то |
k = |
|
|
= |
|
|
. |
|||
|
|
|
3 |
||||||||||
|
|
|
|
|
|
|
|
ds (1 + y′2 ) 2 |
|||||
Как показывает эта формула, для существования кривизны |
|||||||||||||
необходимо, |
чтобы функция |
y = f (x) |
|
была дважды дифференцируема. |
|||||||||
Кроме того, |
эта формула показывает, что кривая имеет положительную |
||||||||||||
кривизну для выпуклых функций. |
|
|
y = x2 |
|
|
||||||||
Пример. |
Найдем кривизну параболы |
|
|
||||||||||
|
|
|
|
k = |
|
2 |
|
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
3 |
|
|
||||
|
|
|
|
|
(1 + 4x2 ) 2 |
|
|
||||||
Из этой формулы видно, |
что |
при |
больших |
значениях x кривизна |
|||||||||
параболы близка к нулю, т.е. парабола «выпрямляется», а наибольшая кривизна будет в начале координат и равна 2 .
24.3.Геометрический смысл кривизны. Назовем радиусом
кривизны для кривой |
в заданной точке величину |
R = |
1 |
. Используя |
||
k |
||||||
|
|
|
|
|
||
формулу кривизны k = |
1 |
для окружности радиуса R , |
дадим следующую |
|||
R |
||||||
|
|
|
|
|
||
геометрическую интерпретацию радиуса кривизны произвольной кривой. Пусть кривизна в данной точке равна k . Через эту точку проведем окружность той же кривизны с центром на нормали к кривой в этой точке.
Радиус |
этой окружности R = 1/ |
|
k |
|
и принимается |
за радиус кривизны |
|
|
|||||
кривой в этой точке. |
|
|
|
|
функции y = cos x и |
|
На |
следующем рисунке |
приведён график |
||||
соответствующая окружность. Кривизна в любой точке вычисляется по формуле
k (x) = |
− cos x |
|
. |
(1 + sin2 x) |
3 |
||
|
2 |
|
1
0.8
0.6
0.4
0.2
0 |
-0.8 -0.6 |
-0.4 -0.2 |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
-1 |
Рис. 24.3
165

В начале координат k(0) = −1. Кривизна отрицательна, так как кривая выпукла вверх. Радиус окружности кривизны R = 1/ −1 = 1 . Центр
окружности расположен в начале координат.
Свойство кривизны изменять своё значение вдоль кривой используется, например, при сопряжении прямолинейных участков железнодорожных путей с закруглениями. Допустим, что прямолинейный участок примыкает к участку, имеющему вид дуги окружности. Причем они в точке соединения имеют общую касательную, т. е. соединение гладкое. Но при движении поезда в этой точке мгновенно возникнет центробежная сила, создавая резкий толчок, что нежелательно. Поэтому такие участки соединяют с помощью некоторой переходной кривой. Вдоль неё кривизна постепенно нарастает от нулевого значения до величины обратной радиусу закругления. Аналогичная ситуация наблюдается при конструировании различного рода зубчатых зацеплений.
24.4. Приближённое решение уравнений. Задача точного решения
уравнения |
|
f (x) = 0 |
для произвольной функции, как правило, |
||
неразрешима. |
Например, |
написав для уравнения x2 − 2 = 0 формулу для |
|||
|
|
|
x1 = |
|
, мы только указали математическую |
одного из |
его |
корней |
2 |
||
операцию, с помощью которой этот корень можно вычислить. Поэтому возникает необходимость приближённого вычисления корня данной
функции. Обычно задают допустимую погрешность |
ε , с которой этот |
|
корень нужно вычислить. Это |
значит нужно найти |
такой промежуток |
[a,b] , содержащий корень ξ |
( f (ξ) = 0 ), что его |
длина b − a < ε. |
Предполагается, что вычисление значений функции |
f (x) проблемы не |
|
составляет.
Рассмотрим несколько методов поиска корней на примере уравнения
f (x) = x3 + x −1= 0 .
Функция f (x) всюду непрерывна. Вычислив f (0) = −1 < 0 и |
f (1) =1 > 0 , |
убеждаемся, что в промежутке [ 0,1] есть, по крайней мере, |
один корень |
нашего уравнения. Покажем, что других корней в этом промежутке нет.
′ |
2 |
+1 |
> 0 положительна, поэтому график |
Производная функции f (x) = 3x |
|
функции один раз пересечёт ось Ox , переходя от отрицательного значения к положительному значению. Иногда эту процедуру «отделения» корня
производят графически. Построим графики функций |
y = x3 |
и |
y |
2 |
= 1 − x . |
|
1 |
|
|
|
Абсцисса точки их пересечения и есть искомый корень (см. рис. 24.4). В нашем случае из рисунка видно, что корень расположен в промежутке 0,6 < ξ < 0,8 , т. е. мы ещё сузили промежуток, где находится корень. Далее применим так называемый метод деления отрезка. Вычисляем значение
166
функции в средине отрезка f (0,7) = 0,343 - 0,300 = 0,043 > 0 и на одном из его концов, например, f (0,6) = 0,36 ×0,6 - 0,4 = -0,184 < 0 .
Следовательно, корень находится в промежутке 0,6 < ξ < 0,7 , т. е. корень вычислен с точностью до 0,1. Ясно, что эту процедуру уточнения значения корня можно продолжить, но она требует слишком большого количества вычислений.
1.4 |
|
|
|
y=x3 |
|
|
|
1.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0.8 |
|
y=1-x |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
-0.2 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
1.2 |
1.4 |
0 |
|||||||
Рис. 24.4
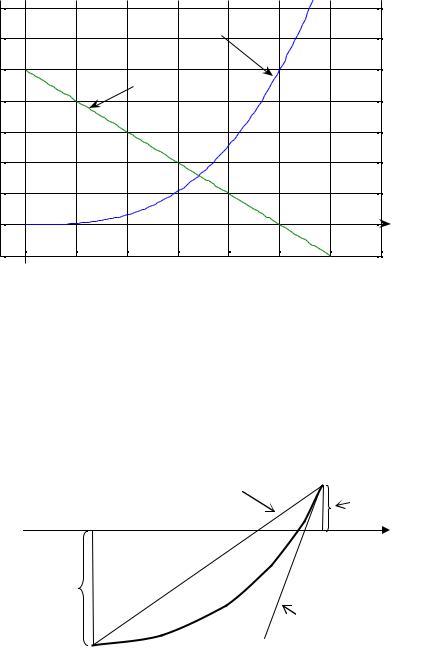
Познакомимся с методами, которые быстрее ведут к цели. Но для их применения нужна дополнительная информация о поведении функции в промежутке, на котором изолирован корень. Заметим, что вторая производная функции f ′′(x) = 6x > 0 положительна, следовательно, график функции в промежутке 0,6 < x < 0,7 имеет вид (см. рис. 24.5)
B
хорда
f (b) = 0.043
a = 0.6
b = 0.7
f (x)
f (a) = −0.184
касательная
A
Рис. 24.5
Если провести хорду АВ , то точка a1 пересечения хорды с осью Ox даст очередное приближение к искомому корню слева. Приближение справа
167
можно получить, найдя точку пересечения b1 касательной (проходящей
через точку В ) с осью Ox . Запишем уравнение хорды АВ как уравнение |
||||||||
прямой, проходящей через две точки |
|
|
|
|
|
|||
|
|
y − f (a) |
= |
x − a |
, |
|||
|
|
f (b) − f (a) |
|
|
||||
|
|
|
|
b − a |
||||
которое в данном случае примет вид |
|
|
|
|
|
|||
|
|
y + 0,184 |
= |
x − 0, 6 |
. |
|||
0, 227 |
|
|||||||
|
0,1 |
|
|
|||||
Отсюда при y = 0 получаем |
a1 ≈ 0,681. Уравнение касательной в точке |
|||
В имеет вид |
|
′ |
|
|
|
|
|
|
|
|
y − f (b) = f (b)(x − b) |
|
||
или |
y − 0,043 = 2,47(x − 0,7) . |
|
||
|
|
|||
Полагая |
y = 0 , получаем |
b1 ≈ 0,683 . Проверим, |
не «потеряли ли» мы |
|
корень, |
взяв приближенные значения |
a1 и b1 . |
Для этого подсчитаем |
|
значения функции в этих приближённых значениях |
|
|||
|
f (0,681) = −0,003K< 0, |
f (0,683) = 0,002K> 0 . |
||
Значения функции на концах промежутка [0,681; 0,683] оказались разных знаков. Значит, мы вычислили корень с точностью ε = 0,002 . Если же в качестве приближённого значения корня взять среднее арифметическое
ξ = (a1 + b1 ) / 2 = 0, 682 , то корень будет вычислен с точностью ε = 0,001.
168
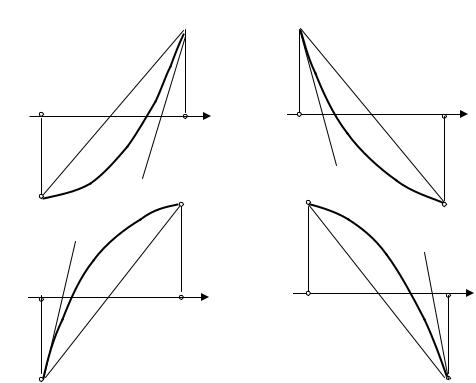
f ′ < 0
f ′ > 0 
 f ′′ > 0 f ′′ > 0
f ′′ > 0 f ′′ > 0
a |
b |
a
b
f ′ < 0
f ′ > 0 f ′′ < 0 f ′′ < 0
a |
b |
b |
a |
Рис. 24.6
Эту процедуру уточнения корня методом хорд и касательных можно продолжить, однако с методом касательных нужно быть внимательнее. Построив касательную не в той точке промежутка, можно не приблизиться к корню, а удалиться от него (см. рис 24.6). На рисунке хорды проведены пунктирной линией. Анализ возможных ситуаций показывает, что касательную нужно проводить из той точки кривой y = f (x) , в которой знак функции совпадает со знаком второй производной.
Раздел 5. Аналитическая геометрия. Кривые и поверхности второго порядка
Лекция 25. Линии второго порядка
До сих пор в аналитической геометрии мы изучали прямые и плоскости, в уравнения которых переменные x , y и z входят в первой степени. Сейчас переходим к рассмотрению кривых на плоскости, задаваемых более сложными алгебраическими уравнениями, включающими вторые степени текущих координат x и y или их взаимное произведение.
Уравнение вида
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0 |
(25.1) |
169
