
9175
.pdf
5). Моменты инерции сечения относительно осей х и у
Jx = ∑( Jx i + Ai ai2 ) = [6400 + 48 · 1.052] + [115 + 26.8 ·16.052] +
+ [1520 + 23.4 · (-8.95)2] + [51.68 + 15.67 · (-17.31)2] = 21613.04 см4,
Jy |
= ∑( Jy i + Ai bi2 ) = [5.76 + 48 · (-2.5)2] + |
[1840 + 26.8 · 8.12] + |
|
|
|
||||||||||||||
|
|
+ [113 + 23.4 · 0.172] + [155.52 + 15.67 · (-6.47)2] = 4829.27 см4, |
|
|
|||||||||||||||
Jxy |
= ∑( Jx i y i + Ai ai bi |
) = [0 + 48 · 1.05 · (-2.5)] |
+ [0 + 26.8 ·16.05 · 8.1] |
+ |
|
||||||||||||||
|
|
+ [0 + 23.4 · (-8.95) · 0.17] + [51.18 + 15.67 · (-17.31) · (-6.47)] = 5128.68 см4. |
|||||||||||||||||
6). Главные центральные моменты инерции заданного сечения |
|
|
|||||||||||||||||
|
|
|
|
|
J max |
= J1,2 = |
Jx + Jy |
|
± |
1 |
[(Jx - Jy )2 + 4 J 2xy ] = |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
min |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
21613.04 + 4829.27 |
± |
1 |
|
[(21613.04 - 4829.27)2 + 4×5128.68 2 ] |
= 13221.16 ± 9834.99. |
|||||||||||||
|
|
|
|||||||||||||||||
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Jmax |
= J1 = 23056.15 см4, |
|
Jmin = J2 = 3386.17 |
|
см4. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверка: Jx + Jy = 21613.04 + 4829.27 = 26442.31 см4,
J1 + J2 = 23056.15 + 3386.17 = 26442.32 см4.
7). Углы наклона главных центральных осей инерции сечения |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
tgα max |
= |
|
|
Jxy |
|
|
= |
|
|
|
|
|
5128.68 |
|
= - 0.28138, |
|
α max |
= -15.72 |
o |
. |
|
|
||||||||||||||||
|
Jy |
|
|
|
|
|
4829.27 - 23056.15 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
- Jmax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
tgα min |
= |
|
|
Jxy |
|
|
|
= |
|
|
|
|
|
|
5128.68 |
|
|
= 3.5539325, |
|
αmax |
= |
74.28 |
o |
. |
|
|
||||||||||||
Jy |
|
|
|
|
|
4829.27 - 3386.17 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
- Jmin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Проверка: |
|
αmax |
|
+ |
|
α min |
|
= 15.72o + 74.28o = 90o. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
8). Главные центральные радиусы инерции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
imax |
= |
|
|
Jmax |
|
= |
|
23056.15 |
|
= 14.23 см, |
imin = |
Jmin |
|
|
= |
|
3386.17 |
|
= 5.45 см. |
||||||||||||||||||
|
|
|
A |
113.87 |
A |
113.87 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
у4 |
|
у1 |
у3 |
|
|
|
|
у2 |
|
|
|
|
3.97 см |
|
2.67 см |
min (2) |
|
|
|
|
|
|||
|
|
|
|
10.60 см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х2 |
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
2.50 см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
.2 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
= |
7 |
|
|
|
|
|
|
|
|
|
|
|
IN |
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
c |
1 |
|
|
|
|
|
|
|
|
х1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
MAX = - |
15. |
72 |
O |
х |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max (1) |
|
|
|
|
|
|
|
|
|
|
|
|
х3 |
|
|
|
|
c3 |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
х4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
3.37 см |
|
|
|
|
|
|
20.00 см |
|
|||
10.00 см |
1.20 см |
7.60 см |
|
|
|
|
|
|
|
|||
|
|
|
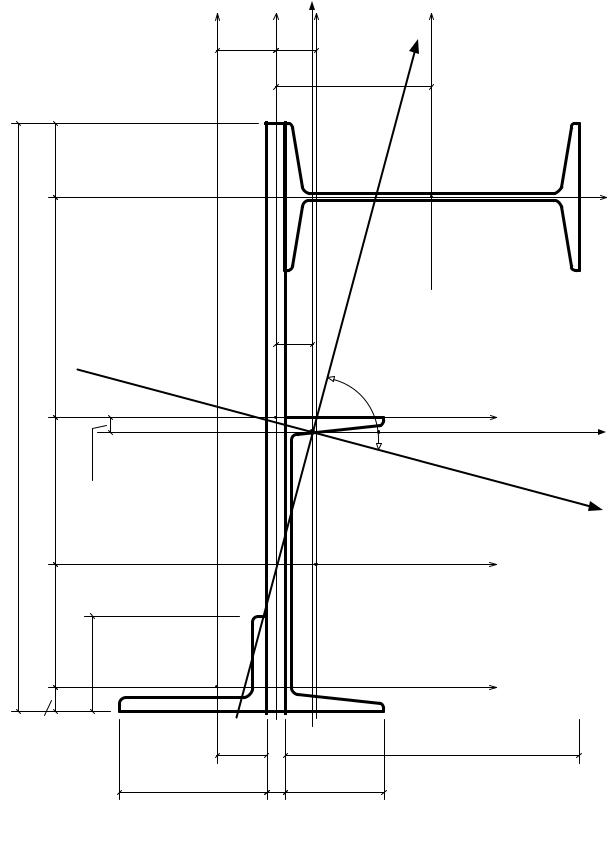
Рис.2.12 |
|
|
|
|
|
|
|
|
|

Пример 2.3 Для заданного поперечного сечения стержня, состоящего из следующих фигур:
1.полукруга с диаметром 8 см;
2.равнобедренного треугольника 6х9 см;
3.прямоугольного отверстия 2х3 см;
необходимо определить:
-положение центра тяжести поперечного сечения (т. С);
-главные центральные оси поперечного сечения;
-главные центральные моменты инерции поперечного сечения;
-моменты сопротивления сечения.
Ре ш е н и е.
Вычисление геометрических характеристик фигур, составляющих заданное сечение, выполне-
но и представлено в таблице.
1). Определяем общую площадь заданного сечения
А = А1 + А2 – А3 = 25.13 + 27 - 6 = 46.13 см2.
2). Определяем статический момент сечения относительно оси х1.
Sx 1 = y1 A1 + y 2 A2 - y3 A 3 = 0 + (-4.7) ×27 - (-3.2) ×6 = -107.7 см3 .
3). Определяем координаты центра тяжести заданного сечения.
Поскольку заданное сечение имеет ось симметрии (ось у), то центр тяжести располагается на
этой оси, поэтому необходимо определить только координату ус
yc = Sx 1 = - 107.7 = - 2.335 см . A 46.13
4). Через полученный центр тяжести проводим горизонтальную ось х.
Оси х, у является искомыми главными центральными осями инерции заданного сечения, т.к.
ось у – ось симметрии и Jxy = 0.
5). Вычисляем главные центральные моменты инерции сечения
J |
x |
= (J |
x 1 |
+ a2 |
A |
1 |
) + (J |
x 2 |
+ a2 |
A |
2 |
) - (J |
x 3 |
+ a2 A |
3 |
) = [0.28 ×100.53 + 2.335 2 |
×25.13 ] |
+ |
|||||||
|
|
1 |
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
||||||||
+ |
|
[121.5 + (- 2.365) 2 ×27] - |
[4.5 + (- 0.865) 2 ×6] = 428.69 см4 , |
|
|
|
|
|
|
Из |
|||||||||||||||
Jy |
= Jy |
1 |
+ Jy |
2 |
- Jy |
= 100.53 + 40.5 - 2 = 139.03 см4 , Jxy = Jx y |
1 |
+ Jx |
y |
2 |
- Jx |
y |
= 0 . |
||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
|
3 |
||||
полученного решения следует:
Jmax = J1 = Jx = 428.69 см4, Jmin = J2 = Jy = 139.03 см4 .
6). Вычисляем осевые моменты сопротивления сечения
Wx( 1) = |
Jx |
= |
428.69 |
= 92.49см3 , |
Wx( 2 ) = |
|
|
Jx |
|
|
= |
428.69 |
= 51.25см3 , |
||||||||
y1 |
|
|
|
y2 |
|
|
|
||||||||||||||
|
|
|
|||||||||||||||||||
|
4.635 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8.365 |
|
|||||
|
|
|
|
W |
|
= |
|
Jу |
|
= |
139.05 |
= 34.76см3 . |
|||||||||
|
|
|
|
у |
|
х |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2.13 |
|
|
|
|
|
|
|
|
|||
2.30 |
|
|
|
|
|
|
|
|
|
3.00 |
|
|
|
|
|
1.50 |
|
|
|
|
|
1.70 |
|
|
|
|
|
|
|
|
|
6.00 |
|
|
|
|
|
1.50 |
|
|
|
|
|
A1 = |
π 82 |
=25.13см |
2 |
|
|
|
|
|
|
|
|
|
A 3 = 2× 3 = 6см2 |
|
|||||||
8 |
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||
|
=0.28 π 84 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
J x1 |
=0.28×100.53см4 |
A 2 = |
2 ×6 |
× 9 = 27 cм2 |
|
|
Jx3 |
= 2×33 |
= 4.5 см4 |
||||||||||||
|
|
π 8 |
4 |
128 |
|
|
|
Jx2 |
= |
6×93 |
=121.5 см |
4 |
|
|
|
12 |
3 |
|
|
||
Jy1 |
= |
|
=100.53см |
4 |
36 |
|
|
|
|
Jy3 |
= |
3 ×2 |
|
=2см |
4 |
||||||
128 |
|
|
|
3 |
|
|
12 |
|
|
||||||||||||
|
|
|
|
|
|
|
= 9×6 |
|
|
|
|
|
|
|
|||||||
J x1y1 =0 |
|
|
|
|
|
Jy 2 |
|
|
= 40.5 см4 , Jx2 y 2 |
= 0 |
Jx3y3 =0 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
48 |
|
|
|
|
|
|
|
|
|
|
|
3. Определение внутренних сил в стержнях
3.1Внешние и внутренние силы
Силы в сопротивлении материалов принято разделять на силы, действующие на конст-
рукцию извне (внешние силы) и силы, возникающие в результате взаимодействия частей конструкции между собой (внутренние силы).
3.1.1 Активные и реактивные внешние силы
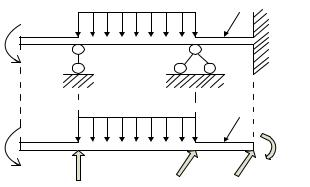
Рассмотрим тело (рис.3.1), у которого один размер значительно превышает два других
(стержень или брус). На него действует внешняя нагрузка: q, F, М. Это активные силы.
Рис.3.1
Стержень имеет опоры А, В и С (рис.3.1а). Силы, с которыми опоры воздействуют на брус, по отношению к нему также являются внешними. Это реакции (реактивные силы): RA
,RB, Rc, Мс (рис.3.1б).
3.1. 2 Система координат.
Оси х и у будем считать главными центральными осями сечения и располагать в его плоскости. Ось z в этом случае будет направлена по оси стержня (геометрическое место цен-
тров тяжести всех поперечных сечений стержня) .
3.1.3 Определение опорных реакций.
Для определения n опорных реакций необходимо составить n уравнений равновесия,
следя за тем, чтобы уравнения были независимыми друг от друга. Для произвольной систе-
мы сил на плоскости можно составить три линейно независимых уравнения равновесия. Для системы параллельных сил - лишь два. По направлению связи возникает реакция (рис.3.1).
3.1.4. Эпюры внутренних сил
Если взять для рассмотрения несколько поперечных сечений стержня и в каж-
дом из них найти внутренние силы, то будет видно, что они изменяются в зависимости от расположения сечения. Расположение сечения определяется координатой z. То есть,
усилия являются функциями z, и эти функции могут быть представлены в виде графи-
ков.
Графики функции 
































 называются эпюрами
называются эпюрами
внутренних сил.
При рассмотрении стержня на плоскости Oyz может быть построено только три
эпюры 

















 .
.
Для выполнения расчета на прочность необходимо знать наибольшее значение каждого из усилий и расположение сечений, в которых они этих значений достигают.
Сечения, в которых усилия достигают наибольших значений (по модулю),
принято считать «опасными».
а) Усилие N (продольное усилие).
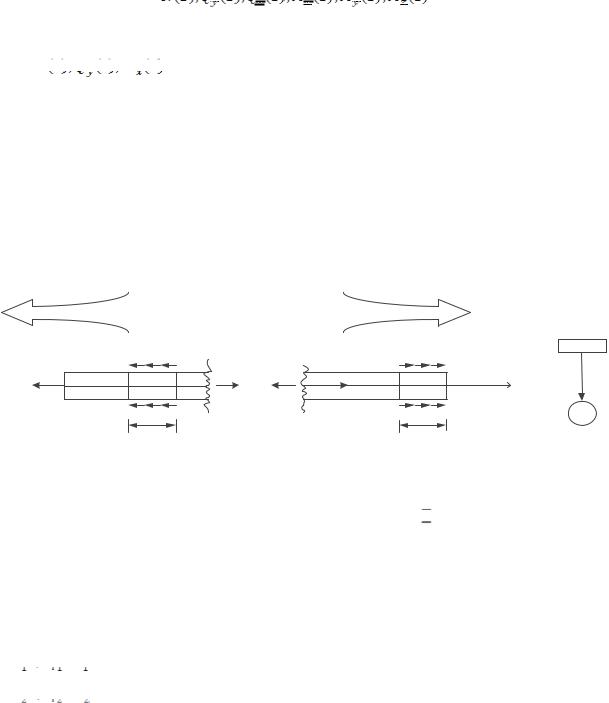
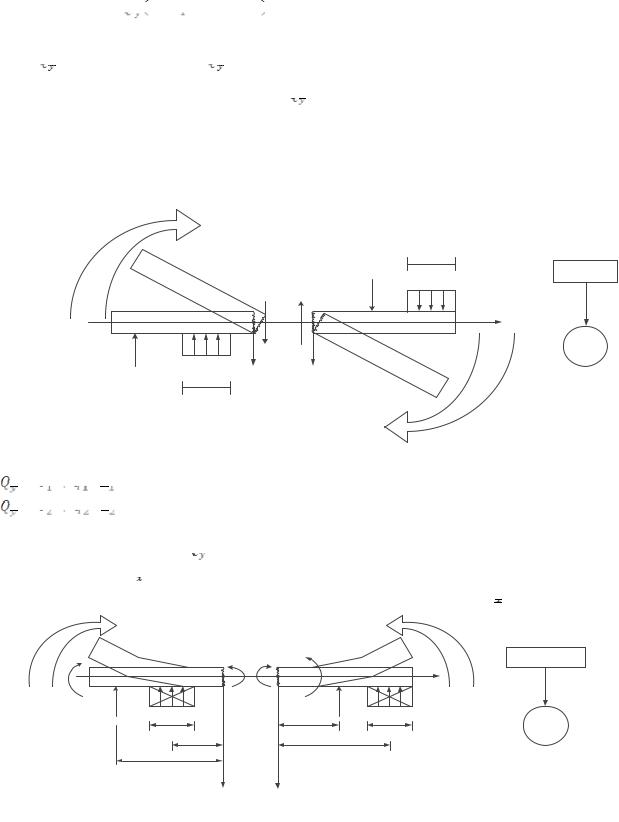
На рис. 3.2 показан рассеченный стержень, в сечении которого возникает поло-
жительное (растягивающее) усилие N.
Рис. 3.2
Неизвестное усилие N должно находиться из уравнения 
 Z = 0, которое состав-
Z = 0, которое состав-
ляется для одной из частей стержня. Чтобы сила N и нагрузка уравновесили друг друга,
они должны быть направлены в разные стороны.
Из рис. 3.2 видно, что внешние силы, вызывающие растягивающее усилие N, на-
правлены «от рассматриваемого сечения». То есть:












 (для левой части стержня),
(для левой части стержня),



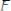








 (для правой части стержня).
(для правой части стержня).
Соответственно, нагрузка, направленная «к сечению», будет вызывать отрица-
тельное усилие N.
б) Усилие 


















На рис. 3.3 показан рассеченный стержень с положительно направленным уси-
лием 
 . Неизвестное усилие
. Неизвестное усилие 
 должно находиться из уравнения ∑Y = 0, составленно-
должно находиться из уравнения ∑Y = 0, составленно-
го для одной из частей стержня. Чтобы 
 и нагрузка уравновесили друг друга, они
и нагрузка уравновесили друг друга, они
должны быть направлены в разные стороны. Из рис.3.3 видно, что внешние силы, вы-
зывающие положительную поперечную силу, стремятся повернуть отсеченную часть стержня “ по часовой стрелке» относительно оси х, проходящей через сечение.
Рис. 3.3
3.3
То есть 









 (для левой части стержня),
(для левой части стержня),









 (для правой части стержня).
(для правой части стержня).
Соответственно, нагрузка, направленная «против часовой стрелки» будет вызывать отрицательное усилие 

 .
.
в) Усилие 

 (изгибающий момент).
(изгибающий момент).
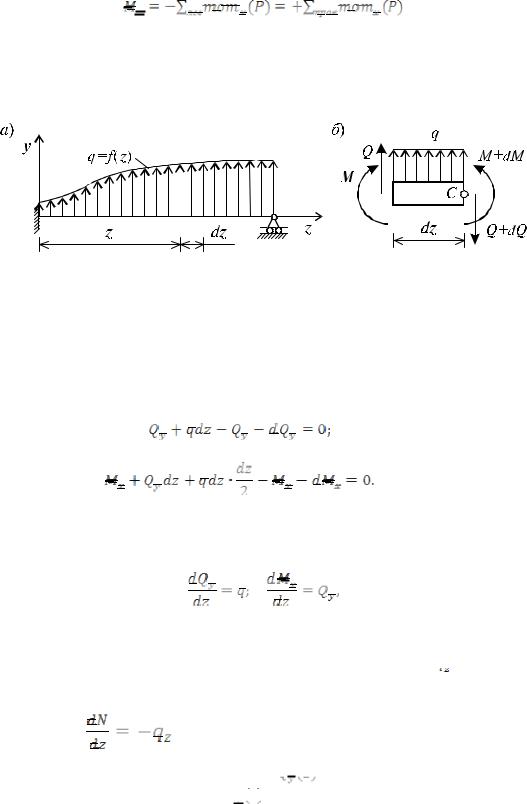
На рис.3.4 показан рассеченный стержень с положительным усилием 

 .
.
Рис. 3.4

Неизвестный внутренний момент 

 следует искать из уравнения равновесия
следует искать из уравнения равновесия








 (х проходит через центр тяжести сечения), составленного для левой или пра-
(х проходит через центр тяжести сечения), составленного для левой или пра-
вой частей стержня. Из рис. 3.4 видно, что, если усилие 

 направлено против часовой стрелки, то уравновешивающая его нагрузка должна давать относительно х момент по часовой стрелке (и наоборот). То есть, другими словами, внешние силы вызывают по-
направлено против часовой стрелки, то уравновешивающая его нагрузка должна давать относительно х момент по часовой стрелке (и наоборот). То есть, другими словами, внешние силы вызывают по-
ложительный изгибающий момент, если стремятся изогнуть часть стержня выпукло-
стью вниз (вызвать растяжение в нижних волокнах стержня). Тогда























 (для левой части стержня),
(для левой части стержня),






















 (для правой части стержня).
(для правой части стержня).
Соответственно, нагрузка, направленная иначе, чем на рис. 4, будет вызывать отрицательное усилие 

 .
.
Нагрузка в виде сосредоточенного момента никогда не входит в выражения для усилий N и 
 , поскольку не входит в уравнения для их определения ∑Y = 0, ∑Z = 0. На любую ось момент, представляющий собой пару разнонаправленных равных сил (рис.
, поскольку не входит в уравнения для их определения ∑Y = 0, ∑Z = 0. На любую ось момент, представляющий собой пару разнонаправленных равных сил (рис.
3.4), всегда проектируется в нуль.
3.1.5 Связь внутреннихи внешних сил
Из уравнения ∑Z = 0, записанного для одной из частей стержня, следует, что продольная сила N равна отрицательной сумме проекций на ось z всех сил, приложен-
ных к левой части стержня, или положительной сумме проекций на ось z всех сил, при-
ложенных к правой части стержня.
Обозначая проекции внешних сил как 
 , запишем
, запишем
(1.1)
Из уравнения ∑у = 0, записанного для одной из частей стержня, следует, что по-
перечная сила 
 равна отрицательной сумме проекций на ось у всех сил, приложенных к левой части стержня, или положительной сумме проекций на ось y всех сил, прило-
равна отрицательной сумме проекций на ось у всех сил, приложенных к левой части стержня, или положительной сумме проекций на ось y всех сил, прило-
женных к правой части стержня.
Обозначая проекции внешних сил как 
 , запишем
, запишем
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.2) |
|
|
|
|
|
|
|
|
|
|
|
|||||
Из уравнения |
|
|
|
|
, записанного для одной из частей стержня, следует, что |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
изгибающий момент равен отрицательной сумме моментов относительно оси х (прохо-
дящей через центр тяжести рассматриваемого сечения) всех сил, приложенных к левой
части стержня или положительной сумме моментов относительно оси х всех сил, при-
ложенных к правой части стержня.
Обозначая моменты нагрузок как momx (P), запишем
. |
(1.3) |
3.1.6 Дифференциальные зависимости Журавского.
Пусть брус нагружен произвольным образом распределенной нагрузкой q=f(z) (рис. 3.5,а).
Рис. 3.5
Выделим из бруса элемент длиной dz и приложим по его краям положительные внутренние усилия (рис. 3.5,б). В пределах малого отрезка dz нагрузку q можно считать распределенной равномерно. Приравняем нулю сумму проекций всех сил на вертикальную ось y и сумму моментов всех сил относительно поперечной оси x, проходящей через точку С (рис. 3.5,б), получим:
Производя упрощения и отбрасывая величины высшего порядка малости, полу-
чим теорему Журавского:
Продольное усилие N также связано с распределенной нагрузкой 

 (действую-
(действую-
щей вдоль оси z) дифференциальной зависимостью
. |
(1.4) |
Положительные значения функций N ( z ) , 



 откладываются вверх. Положи-
откладываются вверх. Положи-
тельные значения изгибающего момента 



 по традиции откладываются вниз.
по традиции откладываются вниз.
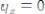
3.2 Построение эпюр продольных сил при центральном растяже- нии-сжатии
Центральным растяжением-сжатием (ЦРС) называется вид сопротивления,
при котором в поперечных сечениях стержня из шести возможных усилий возни-
кает только одно ‒ продольная сила N.
3.2.1 «Аналитический» способ построения эпюр
1.Определяются опорные реакции, если это необходимо.
2.Стержень разбивается на участки. Границами участков являются:
а) края стержня,
б) точки приложения сосредоточенных сил и моментов (включая реакции),
в) границы распределенных нагрузок.
Участки нумеруются последовательно слева направо, а в консольных стержнях - по направлению к заделке.
3.На каждом из участков произвольно выбирается сечение. Его положение задается переменным расстоянием zi (где i- номер участка). Это расстояние отсчитывается обычно от левого или от правого краев стержня.
4.На каждом i-м участке записываются аналитические выражения для усилий, пока-
зывающие, как усилия зависят от расстояния zi. Усилия при этом выражаются через нагруз-
ку, приложенную либо к левой, либо к правой частям стержня (в зависимости от точки от-
счета zi).
5. Полученные функции изображаются графически, для чего сначала подсчитывают-
ся их значения в ряде сечений. Графики усилий (эпюры) строятся на осях, параллельных оси стержня, и штрихуются вертикальной штриховкой. Символами + и - отмечаются знаки усилий. Вычисленные значения наносятся на чертеж. Описанный способ построения эпюр называется «аналитическим».
3.2.2 Правила построения эпюр, согласно дифференциальным зависимостям.
Из дифференциальной зависимости (3.4) следует, что при отсутствии на участке
стержня распределенной продольной нагрузки( |
|
), продольное усилие N постоянно |
|
||
N(z)=const (рис. 3.6). |
|
|
Если на участке приложена постоянная распределенная нагрузка qz(z) = const, из
(1.4) следует, что N(z) изменяется по линейному закону (рис. 3.6) .
