
9096
.pdf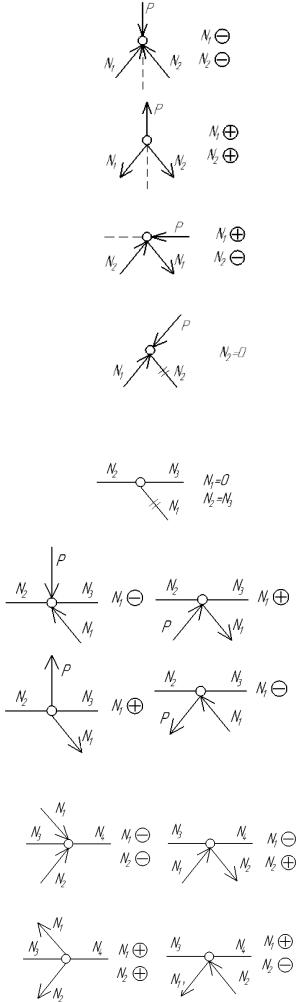
-если линия действия нагрузки проходит внутри узла, образованного стержнями, то знаки усилий в них одинаковы (или оба сжаты при нагрузке, действующей в узел, или оба растянуты – при нагрузке, действующей от узла);
-если линия действия нагрузки проходит вне узла, образованного двумя стержнями, то знаки усилий в них разные – ближайший к силе стержень растянут, другой сжат;
-если линия действия узловой нагрузки совпадает с осью одного из стержней, то примыкающий стержень не работает, а другой стержень может быть сжат или растянут в зависимости от направления действия узловой нагрузки.
б) Трехстержневые узлы
- если в ненагруженном трех стержневом узле два стержня лежат на одной прямой, то усилие в примыкающем стержне равно нулю. Знаки усилий в стержнях, лежащих на одной прямой
всегда однозначны (оба растянуты или сжаты).
- если в нагруженном трех стержневом узле два стержня лежат на одной прямой, а примыкающий стержень и внешняя узловая нагрузка расположены по разные стороны от них, то знак усилия в примыкающем стержне всегда солидарен со знаком узловой нагрузки.
Если внешняя узловая нагрузка и примыкающий стержень расположены с одной стороны от стержней, лежащих на одной прямой, то знак усилия в примыкающем стержне противоположен знаку внешней узловой нагрузки;
в) Четырехстержневые узлы
- если в ненагруженном четырех стержневом узле два стержня лежат на одной прямой, а два примыкающих стержня расположены по разные стороны от них, то знаки усилий в примыкающих стержнях всегда однозначны. Если примыкающие стержни расположены с одной стороны от двух стержней, лежащих на одной прямой, то знаки усилий в примыкающих стержнях всегда разнозначны;
45
- в ненагруженном четырех стержневом узле усилия в стержнях, попарно лежащих на одной прямой, равны по величине и по знаку.
Задания для самостоятельной работы.
Литература: [1, гл. 1]; [4, гл. 1]; [2, гл. 1], [3, гл. 4].
Вопросы для самопроверки
1.Что называется фермой?
2.Какова действительная схема фермы?
3.В каких случаях жесткие узлы фермы могут быть заменены шарнирными узлами?
4.Какие внутренние усилия возникают в стержнях фермы?
5.Классификация ферм по назначению.
6.Какие фермы называются распорными?
7.Какая решетка называется раскосной?
8.Какая решетка называется полураскосной?
9.Какая решетка фермы называется треугольной?
10.По какой формуле определяется число степеней свободы фермы?
11.Как выполнить кинематический анализ фермы?
12.Как проводится структурный анализ решетки фермы?
13.Плоские статически определимые фермы. Классификация ферм, достоинства и недостатки в сравнении друг с другом.
14.Укажите признаки нулевых стержней.
15.Каковы преимущества и недостатки фермы по сравнению с балкой и аркой?
16.Методы определения усилий в стержнях статически определимых ферм. Способ вырезания узлов.
17.Способ моментных точек (простых сечений) для определения усилий в стержнях статически определимых ферм.
18.Способы совместных и замкнутых сечений для определения усилий в стержнях статически определимых ферм.
19.Расчет ферм на подвижную нагрузку: построение линий влияния усилий в стерж-
нях консольных ферм (показать на примере).
20.Частные случаи равновесия узлов ферм (леммы).
10. Арочные конструкции
Арки для несущих конструкций покрытий появились в 40-50 гг. прошлого века. Особенно интенсивно они стали применяться после изобретения стального проката и заклепочных соединений. Основная идея арочных конструкций состоит в следующем. Если криволинейный брус выпуклостью вверх установить на две продольно-неподвижные опоры, то при действии нагрузки на брус на опорах появятся не только вертикальные реакции, но и горизонтальные. Последние принято называть распором. Именно распор в каждом сечении арки создает момент, противоположный по знаку моменту от внешних нагрузок, что и позволяет их существенно уменьшить, а в некоторых случаях довести до нуля.
Арки применяют для покрытий выставочных павильонов, рынков, спортивных сооружений, ангаров, вокзалов и др. В последнее время арочные конструкции применяют и для небольших зданий: теплицы, оранжереи, склады, цехи различного производственного
46
назначения. Пролеты арок колеблются от 15 до 100 м и более, при этом с увеличением пролета экономичность арок возрастает.
По статической схеме арки могут быть трех типов: трехшарнирные статически определимые, двухшарнирные и бесшарнирные – статически неопределимые.
Каждая из них имеет свое преимущество и недостатки. В этой части курса мы рассмотрим только трехшарнирные системы – арки и рамы.
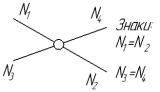
10.1. Образование трехшарнирных арок и рам
Трехшарнирной системой называется система, состоящая из двух дисков, соединенных между собой ключевым шарниром “С” и прикрепленных к основанию с помощью пятовых шарниров “А” и “B”.
Если основание рассматривать как третий диск, то трехшарнирная система будет представлять собой систему из трех дисков, соединенных между собой шарнирами. Такое соединение является геометрически неизменяемым.
Трехшарнирной аркой будем называть систему, состоящую из двух криволинейных стержней, связанных между собой ключевым шарниром и прикрепленных к основанию с помощью двух шарнирно-неподвижных опор.
Трехшарнирные арки, составленные из стержней ломанного очертания, называют трехшарнирными рамами.
Если диски трехшарнирной системы являются фермами, то система называется трехшарнирной арочной фермой.
В трехшарнирных арках при вертикальной нагрузке в опорах возникают, кроме вертикальных, и горизонтальные составляющие опорных реакций. Горизонтальные составляющие опорных реакций называют распором. Распор арки должен восприниматься сооружениями, поддерживающими ее (например, стенами, устоями моста и т.д.), или специальной конструкцией опор. Распор может быть воспринят и самой аркой, если соединить опорные шарниры стержнем-затяжкой. Такая система называется арка с затяжкой. При устройстве затяжки одна из опор арки должна быть выполнена шарнирно подвижной, в противном
47
случае система превращается в статически неопределимую. Затяжка может быть ломаного очертания и расположена выше или ниже уровня опор.
В отличии от сводов, арки имеют небольшую ширину сечения и поэтому относятся к виду брусьев.
Оси арок могут быть очерчены по дуге окружности, параболе, эллипсу и ряду других кривых. В практике строительства широко применяют параболические и круговые арки.
Геометрические характеристики арок:
Параболическая
y |
4 f |
x (l x); y/ tg |
4 f |
(l 2 x); |
|||||
l2 |
l2 |
||||||||
|
|
|
|
|
|
|
|||
cos |
1 |
|
; sin cos tg . |
||||||
|
|
|
|||||||
1 tg |
|||||||||
|
|
|
|
|
|
|
|||
Круговая
y |
|
R2 ( |
l |
x)2 R f ; |
|
|||
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
R |
f |
|
|
l2 |
l 2 x |
|
||
|
|
|
|
|
;sin |
|
; |
|
2 |
|
|
2 |
|||||
|
|
8 f |
|
|||||
cos y R f R
Основной геометрической характеристикой арки является отношение стрелы подъема арки f – расстояния по вертикали между центром ключевого шарнира “С” и линией, соединяющей центры опорных шарниров, к длине пролета l. Это отношение может изме-
няться в очень широких пределах: для пологих арок |
f |
|
1 |
|
1 |
; для высоких арок |
||||
l |
|
|
||||||||
|
|
|
|
|
4 |
10 |
|
|||
|
f |
|
1 |
1. |
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|||
|
4 |
|
|
|
|
|
|
|
||
48
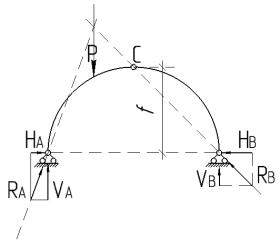
10.2. Аналитический расчет трехшарнирных арок на неподвижную вертикальную нагрузку
Рассмотрим параболическую трехшарнирную арку сплошного сечения с опорами, расположенными на одном уровне и загруженную системой вертикальных сил.
Расчет начинаем с определения опорных реакций. Для определения четырех неизвестных составляющих опорных реакций используем три условия равновесия в форме:
|
|
|
MA 0, |
MB 0, |
x 0 , |
||||
|
|
|
а также дополнительное уравнение, приравняв |
||||||
|
|
|
нулю момент односторонних сил относитель- |
||||||
|
|
|
но ключевого шарнира “С’ MCлев.(прав.) 0. |
||||||
|
|
|
Будем иметь: |
|
|
||||
|
|
|
|
n |
|
|
|
|
|
MA 0: |
|
n |
|
Pi |
ai |
|
|
||
VB |
l Pi ai 0, откуда: VB |
i 1 |
|
|
; |
|
|
||
l |
|
|
|
|
|||||
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
MB |
|
n |
|
|
|
Pi bi |
|
|
|
0: |
VA l Pi bi |
0, откуда: VA |
|
i 1 |
; |
|
|||
|
|
||||||||
|
|
i 1 |
|
|
|
|
l |
|
|
x 0: |
HA HB H. |
|
|
|
|
|
|
|
|
Если рассмотреть вместо арки балку того же пролета и с той же нагрузкой, то можно убедиться, что вертикальные опорные реакции будут определяться теми же первыми двумя зависимостями. Именно поэтому вертикальные составляющие опорных реакций в арке называют балочными реакциями.
Из третьего уравнения видно, что при вертикальной нагрузке горизонтальные составляющие опорных реакций равны по величине и противоположны по направлению.
Из условия равенства нулю изгибающего момента в ключевом шарнире “С” полу-
чим:
MCлев. 0: |
лев. |
VA l Pi (li ai ) H f 0. |
Первые два члена этого уравнения представляют собой балочный изгибающий момент в сечении под ключевым шарниром от левых вертикальных сил, действующих на ар-
лев. |
|
|
O |
||
ку, т.е. VA l Pi (li ai ) MCO . |
Следовательно: H |
MC |
. Из этой формулы сле- |
||
|
|||||
|
|
|
f |
|
|
дует, что величина распора зависит при заданной нагрузке от взаимного расположения шарниров A, B и C, т.е. от пролета lи стрелы подъема f и не зависит от формы очертания каждой из полуарок.
Определим изгибающий момент Mx в произвольном сечении арки, расположенном на расстоянии “x” от левой опоры. С этой целью рассмотрим левую от сечения часть арки
49
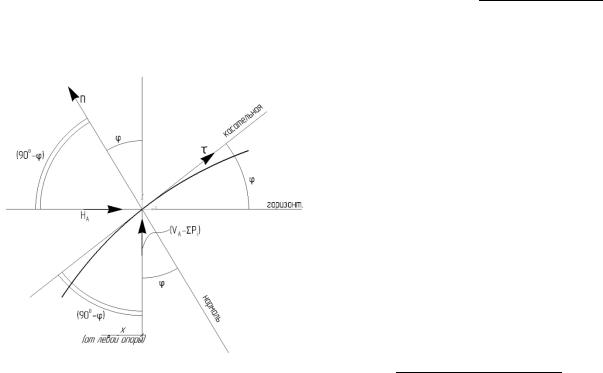
и выразим изгибающий момент в изучаемом сечении как алгебраическую сумму моментов всех сил, расположенных слева от сечения, относительно центра его тяжести:
лев.
Mx VA x Pi (x ai ) H yx.
Выражение, стоящее в скобках, представляет собой балочный изгибающий момент
лев.
MxO в том же сечении, т.е. MxO VA x Pi (x ai ). Следовательно: Mx MxO H yx.
Поперечная сила в произвольном сечении арки равна алгебраической сумме проекций всех односторонних сил на нормаль к оси арки в изучаемом сечении.
В изучаемом сечении проведем касательную к оси арки и нормаль к ней. Проектируя односторонние, например левые, силы на нормаль к оси арки в сечении на расстоянии x от левой опоры, определим поперечную силу:
лев.
Qx (VA Pi ) cos H cos(90 ).
лев.
Выражение (VA Pi ) представляет со-
бой поперечную силу в том же сечении од-
нопролетной балки. Обозначая ее через Qxo
, получим: Qx Qxo cos H sin .
Продольная сила в сечении арки равна алгебраической сумме проекций всех односторонних внешних сил на касательную к оси арки в изучаемом сечении.
Проектируя односторонние, например левые, силы в сечении, расположенном на расстоянии x от левой опоры, на касательную к оси арки в этом сечении, получим про-
лев. |
лев. |
||
дольную силу: Nx [(VA Pi ) cos(90 ) H cos ], где: (VA |
Pi ) Qxo . Тогда: |
||
|
Nx [Qxo sin H cos ]. |
|
|
|
|
|
|
Перед выражением продольной силы стоит знак (-), указывающий на сжатие поперечного сечения арки.
Из выражений внутренних усилий следует, что изгибающие моменты и поперечные силы в трехшарнирных арках за счет наличия распора меньше тех же усилий в балках при одинаковых пролетах и нагрузке. Однако в арках существенное значение приобретают продольные силы Nx , которые в балках при вертикальной нагрузке равны нулю.
Полученные формулы позволяют определять в любом сечении трехшарнирной арки изгибающий момент, поперечную и продольную силы и по их значениям строить эпюры.
На рисунке приведены эпюры изгибающих моментов, поперечных и продольных си от заданной нагрузки.
50
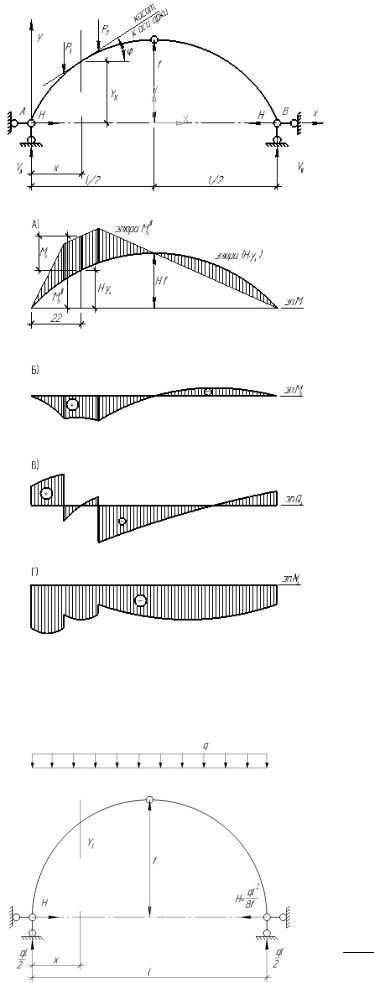
На рис.A построена эпюра изгибающих моментов в арке путем наложения двух эпюр. Первая из них представляет эпюру изгибающих момен-
тов Mxo для простой балки (рис. Б).
Вторая эпюра представляет кривую, подобную кривой оси арки, каждая ордината которой равна распору, умноженному на подъем арки в этом сечении, т.е. на величину (H. yx) (рис. В). После наложения этих эпюр, ординаты откладываем от горизонтали. В результате получаем эпюру M в арке (рис. Г).
10.3. Рациональная ось арки
Рациональным очертанием оси арки называют такое очертание, при котором изгибающие моменты в любом сечении равны нулю и арка работает лишь на осевое сжа-
тие.
Рассмотрим, например, вопрос о рациональном очертании трехшарнирной арки при загружении ее вертикальной равномерно распределенной нагрузкой.
Изгибающий момент в любом сечении арки определяется по формуле: Mx MxO H yx.
Из условия MxO H yx 0получим, что
M O
y x . Следовательно, при вертикальной
x H
51
нагрузке необходимым и достаточным условием рациональности оси является требование пропорциональности ординат балочной эпюры моментов ординатам очертания оси арки.
В нашем случае MxO |
q l |
x |
q x2 |
|
q |
(l x) x, |
|
|
|
||||
2 |
2 |
2 |
|
|||
|
McO |
|
q l2 |
|
|
|
|
|
q |
(l x) x |
|
4 f |
|
||
а H |
|
. Тогда |
y |
|
|
|
2 |
|
(l x) x, т.е. при рав- |
||||||
f |
8 f |
x |
|
|
|
q l2 |
l2 |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
8 f |
|
|
|
|
номерной нагрузке ось арки будет рациональной, если она очерчена по параболе. Задания для самостоятельной работы.
Литература: [1, гл. 1]; [4, гл. 1]; [2, гл. 1]; [3, гл. 5].
Вопросы для самопроверки
1.Арочные конструкции, их назначение и область применения.
2.Типы арок, их достоинства и недостатки в сравнении друг с другом.
3.Аналитический расчет трехшарнирных арок на неподвижную вертикальную нагрузку (определение опорных реакций и усилий М, Q и N в произвольном сечении арки).
4.Понятие рациональной оси арки.
5.Определение опорных реакций в трех шарнирной арке при действии вертикальной нагрузки.
11. Теория перемещений статически определимых систем
11.1. Понятие о перемещении. Работа внешних сил.
Перемещения, вызванные деформацией элементов конструкции, определяют для проверки жесткости и устойчивости, а также для расчета статически неопределимых конструкций. Именно используя дополнительные уравнения деформаций, выражающих соотношения между перемещениями и внешними силами, определяют усилия в “лишних” связях статически неопределимых систем. В этой связи, теория определения перемещений стержневых систем имеет очень большое значение.
В основу определения перемещений в сооружениях положен принцип возможных перемещений для деформируемой системы.
Перемещением данной точки сооружения называется изменение ее координаты, вызванное деформацией сооружения. Мы будем определять перемещения в линейнодеформируемых системах, подчиняющихся закону Гука и принципу наложения, согласно которому результат действия системы сил равен сумме результатов действия отдельных сил.
Будем различать действительные и возможные (виртуальные) перемещения для си-
лы P .
52
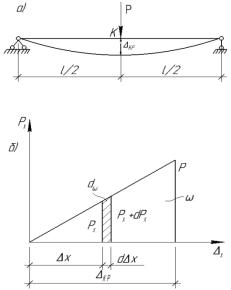
|
|
|
|
|
|
Действительным перемещением точки k |
kp |
||||||||
|
|
|
|
|
|
называют перемещение, вызванное силой P, |
|||||||||
|
|
|
|
|
|
приложенной в точке k (рис. 9.1а). Оно, |
со- |
||||||||
|
|
|
|
|
|
гласно закону Гука, прямо пропорционально |
|||||||||
|
|
|
|
|
|
силе, т.е. kp |
kP |
P, где kP - перемещение |
|||||||
|
|
|
|
|
|
точки k при приложении единичной силы P в |
|||||||||
|
|
|
|
|
|
этой точке в направлении изучаемого переме- |
|||||||||
|
|
|
|
|
|
щения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим статическое приложение силы, |
|||||||||
|
|
|
|
|
|
меняющейся от нуля до окончательного зна- |
|||||||||
|
|
|
|
|
|
чения P (рис. 9.1б). |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Промежуточное значение силы обозначим Px |
|||||||||
, а соответствующее ему перемещение x . |
|
|
|
|
|
|
|
|
|||||||
При изменении силы на dPx , получим приращение в прогибе d x и элементарную |
|||||||||||||||
работу внешних сил dApD |
Px d x . |
|
|
|
|
|
|
|
|
||||||
Когда сила достигла конечного значения P, а перемещение стало равно kP , то |
|
||||||||||||||
действительная работа силы будет определяться интегралом |
|
|
|
|
|
|
|
||||||||
kP |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
ApD Px |
d x d |
P kP . Таким образом, работа AP равна площади за- |
|||||||||||||
|
|||||||||||||||
0 |
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|||
штрихованного треугольника, или: |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||
действительная работа внешней силы P равна половине произведения силы на пе- |
|||||||||||||||
ремещение точки ее приложения по направлению силы |
(теорема Клапейрона). |
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||
|
При наличии ряда сил P1, P2, … , Pn полная работа внешних сил будет равна: |
|
|||||||||||||
|
1 |
n |
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
APD |
|
Pi kPi или учитывая, что kPi Pi kPi получим |
|
APD |
Pi |
2 kPi |
|
||||||||
|
|
|
|||||||||||||
|
2 i 1 |
|
|
|
|
|
|
|
2 i 1 |
|
|
|
|||
Из этой формулы видно, что действительная работа является квадратичной функ- |
|||||||||||||||
цией относительно силы P и поэтому всегда положительная. |
|
|
|
|
|
|
|
||||||||
Возможным (виртуальным) перемещением mn |
называют перемещение точки |
|
|||||||||||||
приложения силы Pm , но вызванное другими силами Pn |
или иными причинами. |
|
|||||||||||||
Для конкретности представления возможных перемещений, рассмотрим процесс приложения двух систем сил в последовательные интервалы времени (рис. 9.2а). Пусть на сооружение в первой стадии действует сила, приложенная статически и меняющаяся от нуля до конечного значения P. При этом вертикальное перемещение точки приложения силы P, которое обозначим PP , является действительным перемещением. Положим, что после действия силы P на сооружение в указанном деформированном состоянии действует также статически новая сила F, которая вызывает дополнительные перемещения точек оси балки (заштрихованы на рис. 9.2а). При этом точка приложения силы P получает добавоч-
ное перемещение PF , величина которого соответствует окончательному значению силы
F. Так как первоначальные перемещения, вызванные силой P, считаем малыми, то доба53
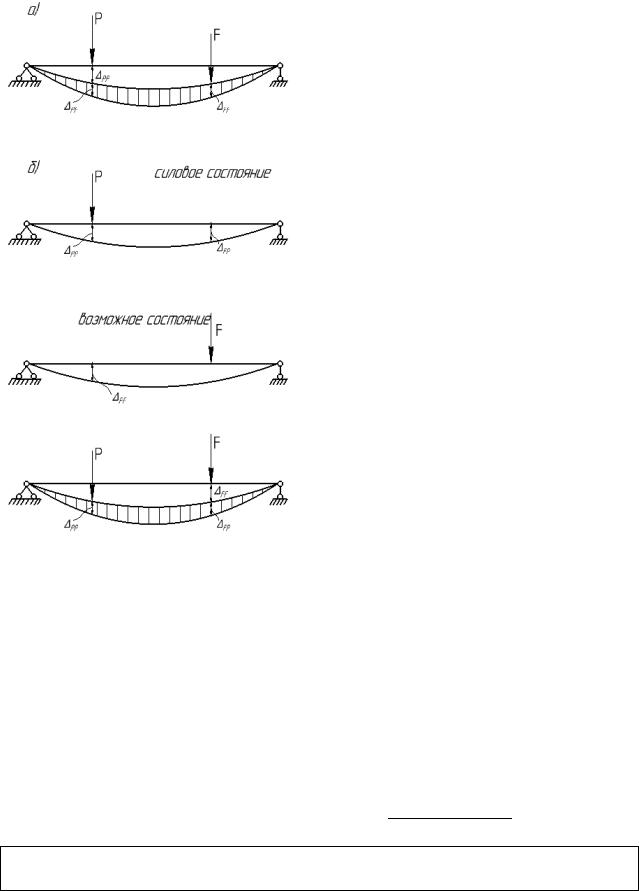
вочные перемещения, вызванные силой F, можно определить от недеформированного состояния и поэтому их можно считать независимыми от силы P.
Перемещение обозначаем PF : первый индекс
“p” обозначает точку приложения перемещения, соответствующего силе P, второй индекс “F” указывает на причину, вызывающую дан-
ное перемещение (сила F). Перемещение PF ,
вызванное в той же системе иной силой F, будет возможным перемещением для силы P. Рассмотрим теперь понятие о возможной работе силы P. Возможной работой силы будем называть работу этой силы на малом возможном перемещении точки приложения силы по ее направлению; для силы P (рис. 9.2а) возможной будет работа силы P на возможном перемещении PF .Так как перемещение PF
не зависит от силы P, то работа силы P выразится произведением силы P на перемещениеPF , т.е. APk P PF . Так как PF не зависит от силы P, то состояние действия силы F можно представить отдельно от состояния действия силы P. На рис. 9.2б показаны два независимых состояния одной и той же балки. Первое состояние – силовое состояние действия данной нагрузки P и второе состояние – возможное состояние действия силы F , на ко-
тором отмечено возможное перемещение PF . Пользуясь этими состояниями, можно оп-
ределить возможную работу силы F второго состояния на перемещении по направлению
этой силы в первом состоянии, т.е. на FP : AFP |
F FP . |
|
||||||||||||||||
|
Выражение для полной работы при последовательном нагружении балки силой P, а |
|||||||||||||||||
затем силой F, будет: A |
1 |
(P |
|
|
F |
|
|
) P |
|
. |
||||||||
|
PP |
FF |
PF |
|||||||||||||||
|
|
|
|
1 |
2 |
|
|
|
|
|
||||||||
|
Если изменить порядок приложения сил, а именно сначала приложить силу F, а за- |
|||||||||||||||||
тем силу P, то получим следующее выражение для полной работы: |
||||||||||||||||||
A |
1 |
(F |
|
P |
|
) F |
|
|
. |
Но от порядка приложения сил величина работы |
||||||||
2 |
FF |
PP |
FP |
|||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
не меняется. Приравняв эти два выражения, получим: P PF F FP .
Равенство формулирует теорему о взаимности возможных работ внешних сил:
возможная работа внешних сил первого состояния на перемещениях, вызванных силами второго состояния, равна возможной работе внешних сил второго состояния на
54
