9008
.pdf
Найти и идентифицировать оптимумы функции
Решение. Сначала найдем первую производную функции:
.
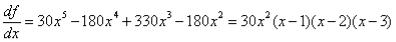Найдем стационарные точки. Для этого решим уравнение: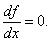 
Следовательно, стационарные точки: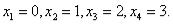 
Найдем вторую производную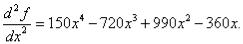 
Для идентификации точек оптимума, вычислим значение второй производной в
стационарных точках.
X |
F(x) |
|
|
|
|
0 |
36 |
0 |
1 |
27.5 |
60 |
2 |
44 |
-120 |
3 |
5.5 |
540 |
Значит, х=1 х=3 – точки локальных минимумов, х=2 – точка локального мак-
симума.
Чтобы идентифицировать точку х=0, найдем и вычислим третью производную:
Так как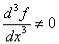 
и N=3 – нечетное, то (по теореме 2, стр.22) х*=0 – точка пере-
гиба.
Задача 2.
Методрм сканирования найти минимальное значение F* и точку минимума Х*
функции F(X)=X4+8X3-6X2-72Х на отрезке [1.5;2]. Точку Х* найти с погрешностью
=0,05.
91
Решение. Будем разбивать первоначальный и новый, удовлетворяющий нас,
интервал на 4 части, при этом новый шаг рассчитываем по формуле:
где n – количество частей деления интервала,
Ai, Bi – концы интервала, в котором содержится максимальное значение функ-
ции, погрешность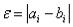 
, где i – номер итерации.
Номер |
|
Концы |
|
|
|
|
Шаг |
новых |
Значение функцииПогрешность |
Примечание |
|||
п. |
||||||
|
интервалов |
|
|
|
||
|
|
|
|
|
||
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
1. |
0,1250 |
1,5000 |
-89,4375 |
0,2500 |
Точность не достигнута |
|
|
|
|
|
|
|
|
1,6250 |
-91,5427 |
|
|
|
|
|
|
|
|
|
|
|
|
1,7500 |
-92,1211 |
|
|
|
|
|
|
|
|
|
|
|
|
1,8750 |
-90,9998 |
|
|
|
|
|
|
|
|
|
|
|
|
2,0000 |
-88,0000 |
|
|
|
|
|
|
|
|
|
|
|
|
2. |
0,0625 |
1,6250 |
-91,5427 |
0,1250 |
Точность не достигнута |
|
|
|
|
|
|
|
|
1,6875 |
-92,0334 |
|
|
|
|
|
|
|
|
|
|
|
|
1,7500 |
-92,1211 |
|
|
|
|
|
|
|
|
|
|
|
|
1,8125 |
-91,7839 |
|
|
|
|
|
|
|
|
|
|
|
|
1,8750 |
-90,9998 |
|
|
|
|
|
|
|
|
|
|
|
|
3. |
0,0313 |
1,6875 |
-92,0334 |
0,0625 |
Точность не достигнута |
|
|
|
|
|
|
|
|
1,7188 |
-92,1290 |
|
|
|
|
|
|
|
|
|
|
|
|
1,7500 |
-92,1211 |
|
|
|
|
|
|
|
|
|
|
|
|
1,7813 |
-92,0070 |
|
|
|
|
|
|
|
|
|
|
|
|
1,8125 |
-91,7839 |
|
|
|
|
|
|
|
|
|
|
|
|
4. |
0,0156 |
1,6875 |
-92,0334 |
0,0313 |
Точность достигнута |
|
|
|
|
|
|
|
|
1,7031 |
-92,0940 |
|
|
|
|
|
|
|
|
|
|
|
|
92
Продолжение таблицы
1 |
2 |
|
3 |
4 |
|
5 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
1,7188 |
-92,1290 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,7344 |
-92,1381 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,7500 |
-92,1211 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
|
|
|
|
|
|
Задача 3. |
|
|
|
|
|
|
|||
Найти |
минимальное |
|
значение F* |
и точку минимума Х* функции |
|||||
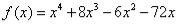на отрезке [1.5; 2]. Точку Х* найти с точностью =0,05.
Решение. Вычисления проведем по формулам представив результаты в таблице
N |
n |
An |
Bn |
X1(n) |
X2(n) |
F(x1(n))F(x2(n)) |
Примечание |
|
|
|
|
|
|
|
|
|
|
1 |
0,309 |
1,500 |
2,000 |
1,691 |
1,809 |
-92,049 |
-91,814 |
|
|
|
|
|
|
|
|
|
|
2 |
0,191 |
1,500 |
1,809 |
1,618 |
1,691 |
-91,464 |
-92,049 |
|
|
|
|
|
|
|
|
|
|
3 |
0,118 |
1,618 |
1,809 |
1,691 |
1,736 |
-92,049 |
-92,138 |
|
|
|
|
|
|
|
|
|
|
4 |
0,073 |
1,691 |
1,809 |
1,736 |
1,764 |
-92,138 |
-92,084 |
|
|
|
|
|
|
|
|
|
|
5 |
0,045 |
|
|
|
1,736 |
|
-92,138 |
|
|
|
|
|
|
|
|
|
|
Первоначальные значения Х1 и Х2 находим по формулам
а значения точности по формуле: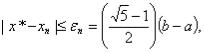 
Из таблицы получаем |
|
|
|
|
Заметим, |
что |
если |
воспользоваться |
формулой |
|
|
то |
необходимое число шагов |
N можно |
|
|
93 |
|
|
определить заранее. В нашем случае N=4,79, т. е. N= 5, и отпадает необходимость во втором столбце таблицы.
Задача 4.
Задача 5.
Задача 6.
Задача 7.
Задача 8.
Задача 9.
Задачи для раздела 3.
Задача 1.
Задача 2.
|
|
|
|
|
|
|
|
|
|
|
|
|
Даны функция u=x2+y2+4x-6y+1, точка M0(-1,2) и вектор a |
4i |
3 j . |
||||||||||
1. |
Найти градиент функции в точке М0 и наибольшую скорость изменения |
|||||||||||
функции в точке М0. Построить градиент. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Вычислить производную функции в точке М0 по направлению вектора a . |
|||||||||||
3. |
Составить уравнение линии уровня функции и построить ее график при а=4. |
|||||||||||
Решение. |
|
|
|
|
|
|
|
|
||||
1. |
Градиентом функции u=f(x,y) в точке М0(х0,у0) называется вектор, координа- |
|||||||||||
ты которого равны значениям частных производных функции в точке М0: |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
du |
|
|
du |
|
|
|
|
|
|
|
gradf (M 0 ) |
|
|
; |
|
|
|
. |
|
|
||
|
|
|
|
|
|
|
||||||
|
|
|
dx |
|
M 0 |
dy |
M |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдем значение частных производных функции в точке М0(-1, 2):
94
du |
(x2 y 2 4x 6 y 1) |
2x 4; |
du |
|
|
|
2; |
|
|
|
|||||
dx |
x |
|
dx |
|
M 0 |
( 1,2) |
|
|
|
|
|
||||
|
|
|
|
|
|
|
du |
(x2 y 2 4x 6 y 1) |
2 y 6; |
du |
|
|
2; |
||||
|
|
|
|||||||||
|
dy |
|
y |
|
dy |
|
M 0 ( 1,2) |
|
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вектор gradf (M |
0 ) 2i |
2 j указывает направление наискорейшего возраста- |
|||||||||
ния функции f в точке М0. Наибольшая скорость возрастания функции f равна модулю градиента:
|
|
|
|
|
|
|
2 |
|
du |
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
du |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
gradf (M 0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ( 2) |
|
2 2. |
||||
|
|
|
|
|
dy |
|
|
|
|
||||||||||||
|
|
|
|
dx |
M |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
|
|
|
|
|
M 0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
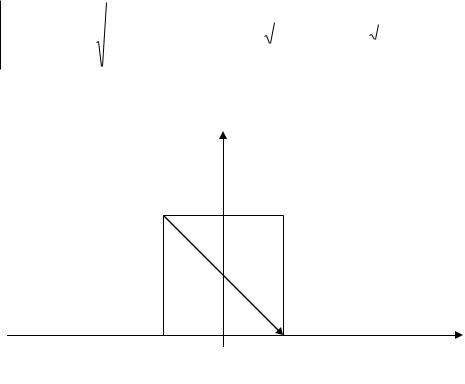
Построим градиент, начало которого находится в точке М0(-1, 2):
у
М0
-1 0 |
1 |
х |
|
|
Задача 3.
Найти локальный экстремум функции z x3 y3 3xy .
Решение. Находим частные производные функции:
zx' 3x2 3y; z'y 3y2 3x
Приравниваем частные производные нулю:
95
|
2 |
3y 0 |
3x |
|
|
|
|
|
3y2 |
3x 0 |
|
|
|
|
Решаем систему уравнений:
|
2 |
3y 0 |
3x |
|
|
|
|
|
3y2 |
3x 0 |
|
|
|
|
|
|
2 |
y x |
|
|
|
|
|
3x4 |
3x |
|
|
|
|
|
y x2 |
|
|
|
|
|
|
1 0 |
0 |
3x x3 |
|
|
|
|
|
x 0 |
|
|
|
|
|
y 0 |
|
x 1 |
||
|
||
|
|
|
|
y 1 |
|
|
|
Имеем две стационарные точки (0,0) и (1,1).
Найдем вторые частные производные:
zx'' 2 6x, zxy'' |
3, |
z''yx 3, z''y2 6 y |
Вычисляем значения вторых частных производных в каждой стационарной точке, составляем определитель и применяем достаточные условия экстремума.
a |
z'' |
2 (0,0) 0, |
a |
z'' |
(0,0) 3, |
a |
z'' |
(0,0) 3, a |
z'' |
2 (0,0) 0 |
11 |
x |
|
12 |
xy |
|
21 |
yx |
22 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
a11 |
a12 |
|
|
0 |
3 |
|
0 0 3 3 9 |
|
|
||
|
|
|
|
a21 |
a22 |
|
|
3 |
0 |
|
|
|
|
|
|
a |
z'' |
2 (1,1) 6, |
|
a |
z'' |
|
(1,1) 3, |
|
a |
z'' |
(1,1) 3, a |
z'' |
2 (1,1) 6 |
||
11 |
x |
|
12 |
xy |
|
|
21 |
yx |
22 |
x |
|
||||
|
|
|
|
a11 |
a12 |
|
|
|
3 |
|
6 6 3 3 27 |
|
|
||
|
|
|
|
6 |
|
|
|
||||||||
|
|
|
|
a21 |
a22 |
|
|
3 |
6 |
|
|
|
|
|
|
Достаточные условия экстремума функции двух переменных:
А) Если >0 и а11<0 (a22<0), то в точке функция имеет максимум; если >0 (a22>0), то в точке минимум.
Б) Если <0, то экстремума нет.
В) Если =0, то вопрос об экстремуме остается открытым.
В точке (0,0) <0, значит, экстремума нет. В точке (1,1) >0 и а11>0, следо-
вательно точка (1,1) является точкой минимума функции. Вычислим значение функции в этой точке.
96
z(1,1) 1 1 3 1
Ответ: (1,1) – точка минимума, z(1,1) 1.
Задача 4. (минимизация функции нескольких переменных методом Ньютона).
Минимизировать функцию f (х) методом Ньютона с заданной точностью
10 3.
f (х) х12 2х22 х12 х22 х32 ехр(х22 х32 ) х2 х3
97
98
99
Задача 5.
Задача 7.
Задача 8.
100