8965

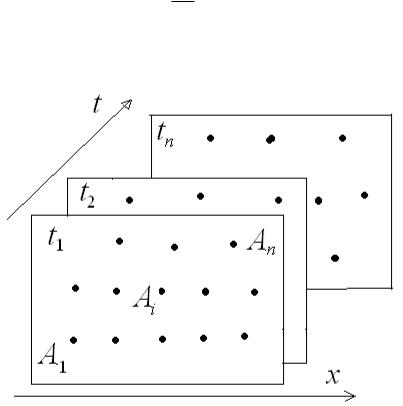
Многомерность статистических данных состоит в том, что у каждого наблюдаемого объекта Ai (X1, X2 , X3 ,..., Xm ) , измеряется (фиксируется) не-

сколько величин-факторов X j j 1, m . Измерения могут проводиться как

одновременно по n однотипным объектам (пространственные ряды данных), так и n измерений одного объекта в разные моменты времени (временные ряды данных) рис.3.3.

Рис. 3.3. Пространственные и временные ряды данных образуют куб данных

Каждый объект, в своѐм ряду данных, представляется вектором измерений

Используя все измерения по n объектам, можем вычислить числовые характеристики по каждому измеримому фактору.

Зная средние значения x j и среднеквадратические отклонения ζx j по каждому измеримому фактору, проведѐм центрирование и нормирование перемен-

33

для всех измеряемых факторов, такой вид матрицы измерения, как увидим далее, позволяет упростить ряд статистических формул. Поэтому в дальнейшем будем пользоваться именно стандартной формой матрицы измерений, а штрихи будем отпускать. При необходимости всегда можно пересчитать все получаемые величины в реальный масштаб по формуле xij xj ζx j xij .

Помимо преобразования в стандартную форму, рекомендуется проверить измерения на грубые ошибки согласно критерию Смирнова-Греббса

[9-10].

Рассмотрим пример многомерных статистических данных, которые будем анализировать во всех последующих главах. Пример состоит в анализе данных об n=11 земельных участках, проданных на рынке в течение года. Известны данные о следующих m=4 факторах участка:

x1 - урожайность участка (кг/сотка)

x2 - экспертная оценка уровня инфраструктуры участка, x3 - экспертная оценка уровня экологии участка,

Пересчитаем данные по 11 участкам в стандартную форму путѐм центрирования и нормирования факторов, а также проверим засорѐнность данных грубыми ошибками измерений [11].

34

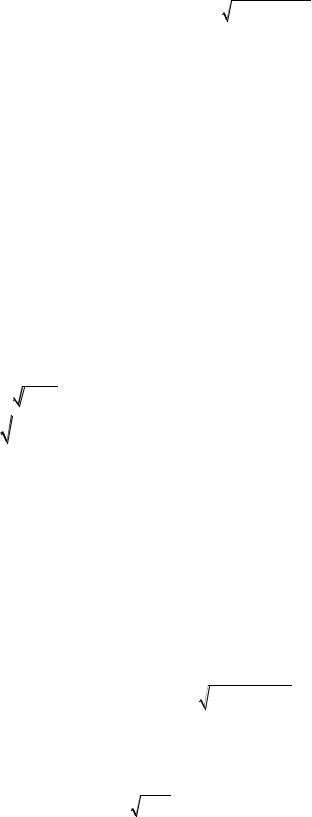
4. Задачи корреляционного анализа

Задачей корреляционного анализа является определение статистической зависимости между наблюдаемыми величинами. Зависимость между величинами

X j и X k определяется империческим коэффициентом парной корреляции

ные коэффициенты корреляции образуют симметричную корреляционную матрицу R :

критерием Стьюдента с уровнем значимости :

эта зависимость является значимой по уровню .

Более строгий корреляционный анализ многомерных данных проводится при помощи частных (очищенных) коэффициентов корреляции. Дело в том, что в многомерных данных парная корреляция двух переменных может быть установлена не по причине их зависимости между собой, а из-за их зависимости от третьей переменной. Частный коэффициент корреляции для переменных X j и

В общем случае частный коэффициент корреляции, очищенный от влияния всех остальных переменных, вычисляется по формулам:

36

5. Задачи регрессионного анализа

Если задачей корреляционного анализа является установление факта зависимости наблюдаемых случайных величин, то задачей регрессионного анализа является установление вида этой зависимости. Выделим из наблюдаемых величин случайную величину Y и постараемся объяснить еѐ значения и свойства че-

рез значения других величин X j . Функционально такую зависимость будем описывать регрессионной моделью:

Y g(X1, X2 ,..., Xm ) ε

Будем величину Y будем называть объясняемой, а величины

назовѐм объяснѐнной частью, а величину ε - необъяснѐнной (специфической, остаточной) частью объясняемой величины. Потребуем в модели для остаточного члена выполнения следующих условий:

Важной проблемой регрессионного анализа является проблема спецификации модели, состоящая в определении состава объясняющих переменных для выбранной объясняемой переменной.

5.1 Линейная среднеквадратическая регрессия

Построим линейную регрессионную модель в виде:

Y β0 β1 X1 β2 X2 ... βm Xm ε .

Коэффициенты теоретической регрессии β j , j 1, m необходимо определить из выше приведѐнных условий А и Б, на основе наблюдательных статистических данных, собранных в матрицу измерений X и измеренный вектор Y объѐма n .

Представим зависимость этих измерений в линейном виде, аналогичном регрессионной модели.

38

здесь yˆ - объяснѐнная часть измерений, а e - невязка измерений и линейной мо-

дели. Подберѐм неизвестные коэффициенты эмпирической регрессии b из условий

Используя то, что наши данные измерений приведены к стандартному масштабу,

Учитывая это, запишем уравнения эмпирической регрессии в индексном и в матричном виде:

yi b1x1i b2 x2i ... bm xmi ei , yi yˆi ei :

y X b e , yˆ X b , e y yˆ .

Запишем также условие минимальности дисперсии невязок в виде:

который показывает, что условие минимальности дисперсии невязок эквивалентно главному принципу метода наименьших квадратов (МНК).

nDe yT y yT Xb bT X T y bT X T X b min

b

Учитывая, что минимум положительно определѐнной квадратичной формы достигается в стационарной точке, получим:

Найденные коэффициенты регрессии b доставляют минимум дисперсии невязки регрессии. Сама невязке вычисляется так:

e y yˆ y Xb y X (X T X ) 1 (X T y) .

Построенная регрессия с коэффициентами b (b1,b2 ,...bm )T , называемая также линейным трендом, объясняет величину y через величины x1, x2 ,...xm не полностью, а лишь частично в силу e 0 . В качестве меры объяснения удобно

39