8908

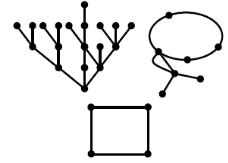
Раздел 3. Теория графов – 4 лекции.

Теория конечных графов – это раздел дискретной математики, иссле-

дующий свойства конечных множеств с заданными отношениями между их элементами. В виде графов можно, например, представить схемы дорог и элек-

трические цепи, географические карты и структурные формулы химических со-

единений, связи между людьми и группами людей.

Определение. Графом G(V , E) называется совокупность двух множеств

{V , E}, где V – множество вершин и E – множество ребер, между элементами которых определено отношение инцидентности P – каждое ребро e E ин-

цидентно ровно двум вершинам v и w V , которые оно соединяет.

Одним из наиболее удобных способов задания графа является геометри-

ческий. Геометрическое представление графа – это схемы, состоящие из то-

чек и соединяющих эти точки отрезков прямых или кривых (примеры графов изображены на рисунке 3.1.).

Рис.3.1. Виды графов

Две вершины v и w называются смежными, если существует соединяю-

щее их ребро е (то есть ребро вида (v, w)); при этом вершины v и w называются

инцидентными этому ребру е (а ребро е – инцидентным этим вершинам).

Аналогично, два различных ребра графа G называются смежными, если они имеют, по крайней мере, одну общую вершину. Смежность и инцидентность – это два бинарных отношения на совокупности всех элементов графа: смежность

– между однородными, а инцидентность – между разнородными элементами.

Каждое ребро инцидентно всегда ровно двум вершинам – своим концам. Вер-

41

шина же может быть инцидентна любому числу ребер.

Граф называется конечным, если множество его элементов (вершин и ре-

бер) конечно, и тривиальным, если его множество вершин V содержит один элемент. В противном случае граф называется бесконечным.

Простой граф – это граф, у которого каждую пару вершин может соеди-

нять не более чем одно ребро.

Существуют графы, в которых две и более вершины могут быть соедине-

ны более чем одним ребром. Ребра, инцидентные одной и той же паре вершин,

называются параллельными или кратными. Ребро, концевые вершины кото-

рого совпадают, называется петлей. Объект, в котором могут быть петли и кратные ребра, называется мультиграфом или просто графом.

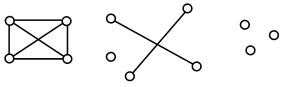
Не всегда точки пересечения ребер принимаются за вершины графа

(рис.3.2). На рис.3.2 а изображен граф с четырьмя вершинами и шестью ребра-

ми, на рис.3.2 б граф с пятью вершинами и двумя ребрами, на рис.3.2 в граф с тремя вершинами, не имеющий ни одного ребра.

дентных ребер, они могут быть инцидентны лишь одной или нескольким пет-

лям. Из всего этого следует, что изолированные вершины недостижимы из лю-

бых других вершин. Висячие вершины – это такие вершины, которые имеют только одно инцидентное ребро. Граф, изображенный на рис.3.8 б, имеет одну изолированную вершину и 4 висячих вершин, а в графе, изображенном на рис.3.8 в, все три вершины изолированные.

Нулевой граф (пустой граф) – граф, не содержащий ни одного ребра, то есть состоящий из одних изолированных вершин. Пустой граф с множеством вершин {1,2,...,n} обозначается через On .

42

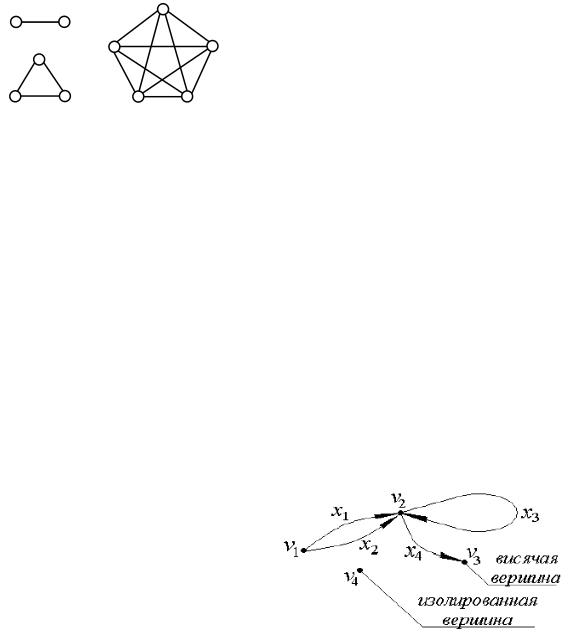
Полный граф – граф, в котором каждые две вершины смежные. Полный граф с множеством вершин {1,2,...,n} обозначается через K n . Граф K1 , в част-

ности, имеет одну вершину и ни одного ребра. В полном графе каждая его вер-

шина инцидентна одному и тому же числу ребер. Если у графа n вершин, то ре-

бер, инцидентных каждой из вершин, будет (n-1). Для задания полного графа достаточно знать число его вершин.

Рис.3.3. Полные графы с n вершинами K2 , K3 , K5

Ребра могут быть ориентированными и неориентированными. Если реб-

ро, соединяющее вершину х с вершиной у , не имеет направления, то оно на-

зывается звеном. Графы, все ребра которых являются звеньями, будем называть

неориентированными или н-графами.

Если для ребра, соединяющего две вершины, указано направление от од-

ной вершины к другой, то в этом случае оно называется направленным (ори-

ентированным), или дугой и изображается стрелкой, направленной от верши-

ны, называемой началом, к вершине, называемой концом. Графы, все ребра ко-

торых являются дугами, будем называть ориентированными или орграфами

(см. Рис.3.4).

Рис. 3.4. Ориентированные графы

Турнир – ориентированный граф, в котором каждая пара вершин соеди-

нена одним ребром.

43

Ор-граф без кратных петель и кратных дуг одного направления называет-

ся графом Бержа.

Понятие бинарного отношения эквивалентно понятию простого (без

кратных дуг) ориентированного графа.

Любой орграф G(V, E) без кратных дуг задает бинарное отношение E на

множестве V, и обратно, пара элементов принадлежит отношению

(vi , v j ) ρ E × E тогда и только тогда, когда в графе G есть дуга

Элементы множества изображаются точками плоскости и образуют мно-

жество вершин графа. Отношения изображаются рёбрами графа: если пара (x,y)

входит в отношение, то из вершины x проводится ориентированное ребро в вершину y.

Граф рефлексивного отношения имеет петли в каждой вершине.

Граф антирефлексивного отношения не имеет петель.

Граф симметричного отношения вместе с ребром, соединяющим x с y, со-

держит ребро, соединяющее y с x.

Граф транзитивного отношения обладает следующим свойством: если из вершины x, двигаясь вдоль рёбер, можно попасть в вершину y, то в графе долж-

но быть ребро, непосредственно соединяющее x с y.

Простой граф (граф без дуг, без петель и кратных ребер) – не что иное,

как антирефлексивное симметричное отношение.

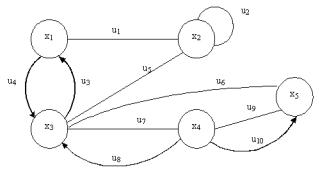
Смешанными (рис.3.5) называются графы, в которых имеются звенья и

дуги.

Рис. 3.5. Смешанный граф

44

Для графа на рис. 3.5 множество вершин V = {х1, х2 , х3 , х4 , х5 }; множество ребер U = {u1, u2 , u3 , u4 , u5 , u6 , u7 , u8 , u9 , u10 }, отношение инцидентности:

P = {(х1 , u1 , х2 ), (х2 , u1 , х1 ), (х2 , u2 , х2 ), (х3 , u3 , х1 ), (х1 , u4 , х3 ), (х3 , u5 , х2 ), (х2 , u5 , х3 ), (х3 , u6 , х5 ), (х5 , u6 , х3 ), (х3 , u7 , х4 ), (х4 , u7 , х4 ), (х4 , u8 , х3 ), (х4 , u9 , х5 ), (х5 , u9 , х4 ), (х4 , u10 , х5 )}

Звенья: u1, u2 , u5 , u6 ,u7 , u9 , u1 и u11; дуги: u3 , u4 , u8 , u10 ; петля: u2 .

Псевдограф – граф, который может содержать петли и/или кратные ребра

(рис. 3.13). Псевдограф без петель называется мультиграфом.

Геометрический граф – это плоская фигура, состоящая из вершин – то-

чек плоскости и ребер – линий, соединяющих некоторые пары вершин. Всякий

граф можно многими способами представить геометрическим графом . На ри-

сунке 3.6 показаны два геометрических графа Γ1 и Γ2 , представляющих, один и тот же обыкновенный граф.

Геометрический граф называется планарным (плоским), если его можно

изобразить на плоскости так, чтобы все точки пересечения ребер этого графа являлись его вершинами. Кроме удобства визуального анализа, есть много за-

дач, где требуется плоское изображение графа. Не все графы являются планар-

ными. Так полный граф К5 и полный двудольный граф К3,3 не являются пла-

нарными.

Если плоскость разрезать по ребрам плоского графа, она распадется на связные части, которые называют гранями.

Грань – область, ограниченная рёбрами в плоском графе, и не содержа-

45

щая внутри себя вершин и рёбер графа. Внешняя часть плоскости тоже образу-

ет грань. Всегда имеется одна неограниченная внешняя грань, все остальные грани называются внутренними.

Двудольный граф (биграф или чётный граф) – это граф G(V,E), такой, что

множество его вершин V разбито на два непересекающихся подмножества V1 и

V2 , причём всякое ребро из E соединяет вершину из V1 с вершиной из V2 , то есть концы каждого ребра принадлежат разным подмножествам. Множества V1

и V2 называются «долями» двудольного графа. Двудольный граф называется

«полным», если любые две вершины из V1 и V2 являются смежными. Если

V1 = a , V2 = b , то полный двудольный граф обозначается Ka,b .

Способы задания графов.

Существует много различных способов задания графов:

1.Явное задание графа в виде двух множеств вершин V и ребер Е, когда каж-

дое ребро определено парой инцидентных ему концевых вершин.

2.Геометрический.

3.Матрица смежности

4.Матрица инцидентности.

5.Список ребер и др.

Кроме теоретико-множественного определения графов и геометрической их реализации существуют еще несколько способов их задания.

В общем виде задать граф – значит указать множества его вершин и ре-

46

бер, а также отношение инцидентности. Для описания вершин и ребер доста-

которой указываются связи между инцидентными элементами графа (ребро

(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки – верши-

нам. Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром (их инцидентность).

а) в случае н-графа:

1, если ребро е инцидентновершине v

εij = − j i

0 в противном случае

б) в случае ор-графа:

Матрица инцидентности однозначно определяет структуру графа, что позволяет читать всю необходимую информацию о графе. Например, выявлять изолированные и висячие вершины, петли; определять степени вершин. Ин-

формация о вершинах считывается по строкам, о ребрах – по столбцам.

Матрица инцидентности н-графа обладает очевидными свойствами:

∙в графе без петель каждый столбец этой матрицы имеет в точности две единицы, соответствующие паре вершин ребра;

∙если в графе имеются петли, то в столбцах, соответствующим пет-

лям, имеется по одной единице, а в остальных по две.

Пример 3.1. По матрице инцидентности определим характеристики гра-

фа:

47

ся как d(x) или deg(x). Максимальная и минимальная степень вершин графа G

выписанных в неубывающем порядке.

Вершина степени 0 называется изолированной, вершина степени 1 назы-

вается висячей (или концевой) вершиной.

Вершина называется нечетной, если ее степень – число нечетное. Вер-

шина называется четной, если ее степень – число четное.

Набор степеней графа на рис. 3.8: (1, 3, 6, 8).

Максимальная степень равна (G)=8, минимальная

δ(G)=1. Чётное число вершин (две вершины: u, z)

данного графа имеют нечётную степень. Сумма сте-

пеней всех вершин равна 18, то есть равна удвоен-

Теорема 1. Сумма степеней всех вершин графа с n вершинами равна уд-

n

военному числу m его ребер: ∑ deg(vi ) = 2m .

i =1

Доказательство: Подсчет всех степеней вершин графа можно вести по вершинам. Возьмем пустой граф. Сумма степеней вершин такого графа равна нулю. При добавлении ребра, связывающего любые две вершины, сумма всех степеней увеличивается на 2 единицы. Таким образом, сумма всех степеней вершин четна и равна удвоенному числу ребер.

Из этой теоремы следует, что каждый граф имеет чётное число нечётных вершин.

Терема 2. (Лемма о рукопожатиях)1. Любой конечный неориентиро-

ванный граф имеет чётное число вершин нечётных степеней.

1 Лемма о рукопожатиях берёт название от популярной аналогии: в группе людей, некоторые из которых пожимают друг другу руки, чётное число людей поприветствовало таким образом нечётное число коллег.

50