
8448
.pdf30
производная П по координатам. Поэтому потенциальную энергию какого-то определенного положения тела считают равной нулю (выбирают нулевой уровень отсчета), а энергию других положений отсчитывают относительно нулевого уровня.
Потенциальная энергия тела обычно определяется работой, которую совершили бы действующие на него внешние силы, преодолевающие консервативные силы взаимодействия, перемещая его из конечного состояния, где потенциальная энергия равна нулю, в данное положение. Работа консервативных сил, приложенных к телу, равна изменению потенциальной энергии этого тела, взятому с обратным знаком, т. е.
dA = — dII, |
(32) |
так как работа совершается за счет убыли потенциальной энергии. Поскольку работа dA есть скалярное произведение силы F на перемещение dr, то выражение (32) можно записать в виде
Fdr = – dII. |
(33) |
Следовательно, если известна функция П(r), то (33) полностью определяет силу F по модулю и направлению.
В случае консервативных сил
F = - ∂П , F = - |
∂П , F = - |
∂П , |
||||
x |
¶x |
y |
|
¶y |
z |
¶z |
|
|
|
|
|||
или в векторном виде |
F = – grad II, |
|
|
|||
|
|
(34) |
||||
где символом grad II обозначена сумма |
|
|
|
|||
grad П = |
∂П i + |
∂П j + |
∂П k |
(35) |
||
|
¶x |
|
¶y |
|
¶z |
|
где i, j, k — единичные векторы координатных осей. Вектор, определяемый выражением (35), называется градиентом скаляра П. Для него наряду с обозначением grad П применяется также обозначение ÑП. Ñ («набла») означает символический вектор, называемый оператором Гамильтона или наблаоператором:
Ñ = |
∂ |
i + |
∂ |
j + |
∂ |
k |
(36) |
|
|
|
|||||
|
¶x |
¶y |
¶z |
|
|||
Конкретный вид функции П зависит от характера силового поля. Например, потенциальная энергия тела массой m, поднятого на высоту h над поверхностью Земли, равна
П = mgh, |
(37) |
31
где h — высота, отсчитанная от нулевого уровня, для которого П0 = 0. Выражение (37) вытекает непосредственно из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты h на поверхность Земли.
Так как начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда положительна!). Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубина h'),
П = – mgh.
Найдем потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна деформации:
Fупр = – kx,
где k — коэффициент упругости (в случае пружины — жесткость), а знак минус указывает, что сила упругости направлена в сторону, противоположную деформации. По третьему закону Ньютона, для преодоления силы упругости надо приложить силу
F = – F упр = kx.
Элементарная работа dA; совершаемая силой F при малой деформации dx, равна
dA = Fdx = kxdx,
а полная работа
x
A = ∫ kxdx = kx 2 / 2 + C = П + C
0
идет на увеличение потенциальной энергии пружины.
Если принять, что потенциальная энергия недеформированного тела (при х = 0) равна нулю, то С = О. Таким образом, потенциальная энергия упругодеформированного тела
П =kx2 /2.
Потенциальная энергия системы, подобно кинетической энергии, является функцией состояния системы. Она зависит только от конфигурации
системы и ее положения по отношению к внешним телам.
Полная механическая энергия системы — энергия механического движения и взаимодействия:
32
Е = Т + П.
3.3.Закон сохранения энергии
Выведем закон сохранения энергии. Для этого рассмотрим замкнутую систему материальных точек.массами m1, m2, … mn, движущихся со скоростями n. Пусть F1', F2’, … , F n’ — равнодействующие внутренних
консервативных сил, действующих на каждую из этих точек, а F1, F2, … , F n — равнодействующие внешних сил. При v « с массы материальных точек постоянны и уравнения второго закона Ньютона для этих точек следующие:
m1 |
dv1 |
|
|
′ |
+ F1 |
dt |
|
|
|||
|
|
= F1 |
|||
m2 |
dv 2 |
|
|
′ |
+ F2 |
dt |
|
|
|||
|
|
= F2 |
|||
. . . . . . . . |
|||||
mn |
dvn |
|
|
′ |
+ Fn |
dt |
|
|
|||
|
|
= Fn |
|||
Пусть все точки за какой-то интервал времени dt совершают перемещения dx1, dx2, … , dx n. Умножим каждое из уравнений скалярно на соответствующее перемещение, и, учитывая, что dxi = vidt, получим
′ |
+ F1 )dx1 |
= 0 |
m1 ( v1dv1 ) − (F1 |
||
′ |
+ F2 )dx2 |
= 0 |
m2 ( v 2dv 2 ) − (F2 |
||
. . . . . . . . . . . . |
||
′ |
+ Fn )dxn = 0 |
|
mn ( vndvn ) − (Fn |
||
Сложив эти уравнения и учитывая, что система замкнута, т. е.
F1 + F2 + … + F n = 0,
получим
n |
n |
′ |
= 0 , |
|
∑ mi vi dvi −∑ Fi dxi |
|
|||
i=1 |
i=1 |
|
|
|
n |
n |
/ 2 ) = dT . |
|
|
∑ mi vi dvi |
= ∑ d( mi vi2 |
(38) |
||
i=1 |
i=1 |
|
|
|
dT - бесконечно малое изменение кинетической энергии всей системы, а
33
n
− ∑ Fi′dxi = dП - бесконечно малая работа всех действующих в системе
i=1
внутренних консервативных сил, взятая с обратным знаком, т. е., согласно (32), бесконечно малое изменение потенциальной энергии системы dII. Следовательно, для всей системы в целом
d T+ dII = О,
откуда полная механическая энергия замкнутой системы
T + П = Е = const. |
(39) |
Выражение (39) представляет собой закон сохранения механической энергии: в замкнутой системе тел, между которыми действуют только
консервативные силы, механическая энергия сохраняется, т. е. не изменяется со временем.
В замкнутой системе тел, силы взаимодействия между которыми
консервативны, взаимные превращения механической энергии в другие виды отсутствуют. Такие системы называются замкнутыми консервативными системами . Существует еще один вид систем — диссипативные системы —
такие системы, в которых механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. Этот процесс получил название диссипации или рассеяния, энергии. Строго говоря, все системы в природе являются. диссипативными. При движении тела в замкнутой консервативной системе происходит непрерывное превращение кинетической его энергии в потенциальную и обратно в эквивалентных количествах, так что полная энергия остается неизменной. Закон сохранения и превращения энергии - фундаментальный закон природы, он справедлив как для систем микроскопических тел, так и для систем микротел.
В замкнутой системе, в которой действуют силы трения, полная механическая энергия системы при движении убывает. Следовательно, в этих случаях закон сохранения механической энергии несправедлив. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой.
3.4.Удар абсолютно упругих и неупругих тел
Примером применения законов сохранения количества движения и энергии при решении реальной физической задачи является удар абсолютно
упругих и неупругих тел.
Удар (или соударение) — это встреча двух или более тел, при которой взаимодействие длится очень короткое время. Исходя из данного определения,
34
кроме явлений, которые можно отнести к ударам в прямом смысле этого слова (столкновения атомов или биллиардных шаров), сюда можно отнести и такие, как удар человека о землю при прыжке с трамвая и т. д. При ударе в телах возникают столь значительные внутренние силы, что внешними силами, действующими на них, можно пренебречь. Это позволяет рассматривать соударяющиеся тела как замкнутую систему и применять к ней законы сохранения.
Прямая, проходящая через точку соприкосновения тел и нормальная к
поверхности их соприкосновения, называется линией удара. Удар называется центральным, если тела до удара движутся вдоль прямой, проходящей через
их центры масс. Мы будем рассматривать только центральные абсолютно
упругие и абсолютно неупругие удары.
Абсолютно упругий удар — столкновение двух тел, в результате которого в обоиx взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию.
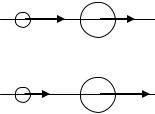
Для абсолютно упругого удара выполняются закон сохранения количества движения и закон сохранения кинетической энергии. Обозначим скорости шаров массами m1 и m2 до удара через v1 и v2, после удара — через v'1 и v'2 (рис. 18). Так как удар центральный, то будем рассматривать модули величин. Законы сохранения имеют вид
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
′ |
|
|
|
m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(40) |
|||
|
|
|
|
|
|
m1v1 + m2 v2 = m1υ1 + m2υ2 |
|
|||||||||||
v1 |
v2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
′2 |
|
m2υ |
′2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
m2 |
|
|
|
|
|
|
m1v1 |
|
+ |
m2 v2 |
= |
m1υ1 |
+ |
2 |
(41) |
|||
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
m1 |
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|
|
||||
v`1 |
v`2 |
|
|
|
|
Произведя соответствующие преобразования |
||||||||||||
|
|
|
|
|
|
|||||||||||||
Рис. 15 |
|
|
в выражениях (40) и (41), получим |
|
|
|||||||||||||
|
|
|
′ |
|
|
|
′ |
+ v2 ) |
|
|
|
|
|
(42) |
||||
|
m1 (υ1 + v1 ) = m2 (υ2 |
|
|
|
|
|
||||||||||||
|
2 |
|
′ |
2 |
) |
2 |
|
′ |
2 |
) |
|
|
|
|
|
(43) |
||
|
m1 ( v1 |
+ υ1 |
|
= m2 ( v2 + |
υ2 |
|
|
|
|
|
|
|||||||
откуда |
|
′ |
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|||
|
υ1 + v1 |
= υ2 + v2 |
|
|
|
|
|
|
|
|
|
|
||||||
Решая совместно уравнения (42), (43) и (44), находим |
|
|
|
|
||||||||||||||
|
υ′ |
= |
( m1 − m2 )v1 + 2m2v2 |
|
|
|
|
|
|
(45) |
||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
|
|
|
|
m1 + m2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
35 |
|
υ |
′ |
= |
( m2 − m1 )v2 + 2m1v1 |
(46) |
|
|
+ m2 |
||||
2 |
m1 |
||||
|
|
|
|
||
Для анализа полученных результатов разберем несколько примеров: 1) при v 2 =0
′ |
= |
m1 |
− m2 |
v1 |
(47) |
||||
|
|
|
|
|
|||||
υ1 |
m1 |
|
+ m2 |
||||||
|
|
|
|
|
|
||||
′ |
= |
|
|
2m1 |
|
v1 |
(48) |
||
|
|
|
|
|
|
||||
υ2 |
|
m1 |
+ m2 |
|
|||||
|
|
|
|
|
|
||||
Проанализируем выражения (47) и (48) для различных масс:
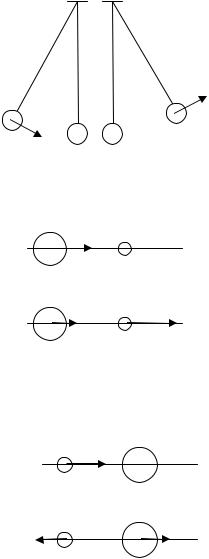
а) m1 = m2. Если второй шар до удара висел неподвижно (v2 = 0) (рис.16), то после удара остановится первый шар (υ'1 = 0), а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался первый шар до
v`2 удара (υ`2 = v1);
v1 |
v2 |
v`2 |
|
||
|
Рис. 16 |
|
m1 |
|
m2 |
|
|
|
|
v1 |
v2=0 |
|
|
|
m1 |
|
m2 |
|
|
|
|
v`1 |
v`2 |
Рис. 17
m1 m2
v1 v2=0
m2
m1
v`1 |
v`2 |
Рис. 18
б) m1 > m2. Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью (υ'1 < υ1). Скорость второго шара после удара больше, чем скорость первого после удара (υ'2 > υ'1) (рис. 17);
в) m1 < m2. Направление движения первого шара при ударе изменяется — шар отскакивает обратно. Второй шар движется в ту же сторону, в которую двигался первый шар до удара, но с меньшей скоростью (рис. 21);
г) m1 >> m2 (например, столкновение со стеной). Из уравнений (47) и (48) следует, что
υ'1 = - v1, υ'2 ≈ 2m1v1/m2 ≈ 0
2) при m1 = m2. Выражения (45) и (46) будут иметь вид
υ'1 = v2, υ'2 = v1,
т. е. шары равной массы обмениваются скоростями.

|
|
|
36 |
|
|
|
m2 |
|
|
|
|
|
|
m1 |
|
Абсолютно неупругий удар — |
столкновение двух |
|||
|
|
|||||
v2 |
тел, |
в результате которого тела объединяются, двигаясь |
||||
v1 |
дальше как единое целое. |
Продемонстрировать абсолютно |
||||
|
||||||
m1+m2 |
неупругий удар можно с помощью шаров из пластилина |
|||||
v |
(глины), движущихся навстречу друг другу (рис. 18). |
|||||
v2, |
Если массы. тел m1 |
и m2, их скорости до удара v1 и |
||||
Рис. 19 |
то используя закон |
сохранения |
импульса, можно |
|||
записать |
|
|
|
|
||
|
m1 v1 + m2 v 2 = ( m1 + m2 )v |
|||||
|
|
|
||||
|
откуда |
m1 v1 + m2 v 2 |
|
|||
|
|
v = |
(49) |
|||
|
|
m1 + m2 |
|
|
||
|
|
|
|
|
|
|
Если шары движутся навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий большим количеством движения. В частном случае, если массы шаров равны (m1 = m2), то
v = (v1 + v2)/2
Выясним, как изменяется кинетическая энергия шаров при центральном абсолютно неупругом ударе. Так как в процессе соударения шаров между ними действуют силы, зависящие не от величины самих деформаций, а от скоростей деформаций, то мы имеем дело с силами, подобными силам трения, поэтому закон сохранения механической энергии не должен соблюдаться. Вследствие деформации происходит потеря кинетической энергии, перешедшей в тепловую или другие формы энергии, Эту потерю можно определить по разности кинетической энергии тел до и после удара:
m v 2 |
m |
v 2 |
|
|
( m + m |
2 |
)v 2 |
||
T = |
1 1 |
+ |
2 |
2 |
|
− |
1 |
|
|
|
|
|
|
|
|
||||
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
Используя (49), получим
T = |
m1m2 |
( v |
1 |
− v |
2 |
)2 |
|
||||||
|
2( m1 + m2 ) |
|
|
|||
|
|
|
|
|
||
Если ударяемое тело было первоначально неподвижно (v2 = 0), то
v = m1v2 m1 + m2
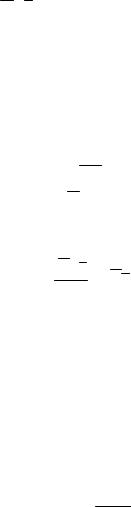
37
T = |
m |
|
|
m v 2 |
|
|
2 |
|
1 |
1 |
|
|
|
||||
|
m1 + m2 |
2 |
|
||
Когда m2 » m1, (масса неподвижного тела очень большая), то v << v1, и почти вся кинетическая энергия дела при ударе переходит в другие формы энергии. Абсолютно неупругий удар — пример того, как происходит потеря механической энергии под действием диссипативных сил.
Краткие выводы
∙Энергия – универсальная мера различных форм движения материальных объектов и их взаимодействия. Количественной характеристикой
процесса обмена энергией между взаимодействующими телами является физическая скалярная величина – работа сил.
Элементарная работа силы
dA = Fd r = F cosα × ds = Fτ ds.
Работа силы на произвольном участке траектории 1-2
2 |
2 |
A = ∫ F cosα × ds = ∫ Fτ ds.
1 |
1 |
·Мощность – физическая скалярная величина, характеризующая скорость совершения работы:
P = dA . dt
Мощность, развиваемая силой F в данный момент времени, равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы:
P = Fdr = Fv.
dt
·Консервативная сила – сила, работа которой при перемещении из одного положения в другое не зависит от траектории перемещения, а зависит только от начального и конечного положений тела. Силовое поле,
в котором консервативные силы совершают работу, называется
потенциальным полем.
·Кинетическая энергия - механическая энергия всякого свободно движущегося тела, численно равная работе, которую совершают действующие на тело силы при его торможении до полной остановки:
Ek = A = mv 2 . 2
·Потенциальная энергия – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

38
∙Связь между консервативной силой F и потенциальной энергией устанавливается выражением
F = − gradЕп,
где
|
∂Еп |
|
|
|
∂Еп |
|
|
|
∂Еп |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
gradЕп = = |
i + |
|
j + |
k . |
||||||||
∂x |
∂y |
|
∂z |
|||||||||
Отсюда, как частные случаи, определяются: а) потенциальная энергия тела массой m на высоте h
Еп = mgh;
б) потенциальная энергия упругодеформированного тела
Еп = kx 2 , 2
где k – коэффициент упругости (для пружины – жесткость).
∙Полная энергия механической системы – равна сумме кинетической и потенциальной энергий:
W= Ek + En .
∙Механические системы, на тела которых действуют только
консервативные силы (внутренние и внешние) называются
консервативными системами. В таких системах выполняется закон сохранения механической энергии:
Ek + En = W = const,
т.е. полная механическая энергия консервативной системы со временем не изменяется. Это фундаментальный закон природы, ко торый является следствием однородности времени.
∙Система, в которой механическая энергия постепенно уменьшается за
счет преобразования в другие формы энергии, называется диссипативной. Строго говоря, все системы в природе являются диссипативными. Однако при уменьшении механической энергии всегда
возникает эквивалентное количество энергии другого вида. Другими словами, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом заключается физическая сущность всеобщего закона сохранения и превращения энергии – неуничтожимость материи и ее движения.
Вопросы для самоконтроля и повторения
1.Что такое энергия, работа, мощность?
2.Как определяется работа переменной силы?
3.Какие силы называются консервативными? Приведите примеры консервативных сил.
4.Какие силы называются диссипативными? Приведите примеры таких сил.
39
5.Дайте определения кинетической и потенциальной энергии.
6.В чем заключается закон сохранения механической энергии? Для каких систем он выполняется?
7.Каким свойством времени обусловлена справедливость закона сохранения механической энергии?
8.В чем физическая сущность закона сохранения и превращения энергии? Почему он является фундаментальным законом природы?
9.Как на основе закона сохранения механической энергии охарактеризовать положения устойчивого и неустойчивого равновесия консервативной системы?
10.Что такое потенциальная яма? потенциальный барьер?
4.Механика твердого тела
4.1.Момент инерции
При изучении вращения твердого тела пользуются понятием момента инерции. Моментом инерции системы (тела) относительно оси вращения
называется физическая величина, равная сумме произведений масс и материальных точек системы на квадраты их расстояний до рассматриваемой
оси:
|
n |
|
|
h |
J = ∑ mi ri |
2 |
(50) |
i=1
dr
В случае непрерывного распределения масс эта сумма
r |
сводится к интегралу |
|
|
|
R |
|
J = ∫ r 2 dm |
Рис. 20
где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами х, у, z.
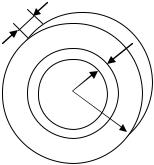
В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис. 20). Разобьем цилиндр на отдельные полые концентрические цилиндры
бесконечно малой толщины dr с внутренним радиусом r и внешним – |
r + dr. |
||||
Момент инерции каждого полого цилиндра |
dJ = r2dm |
(так как dr <<r, то |
|||
считаем, что расстояние всех точек цилиндра от оси равно r), где dm — |
масса |
||||
всего элементарного цилиндра. |
2πrhdr |
— |
объем |
рассматриваемого |
|
элементарного цилиндра. Если ρ — |
плотность материала, то его масса |
|
|||
