
8446
.pdf
80
осуществляется только на изотермах). Оказывается, количество приведенной теплоты, полученной газом за цикл, равно нулю4:
Q1 |
- |
Q2 |
= 0 , |
(48) |
|
|
|||
T1 |
|
T2 |
|
|
что означает также независимость приведенного количества теплоты от пути процесса, а только от начального и конечного состояний, т.е. является функцией состояния. Математическим языком о том же самом можно сказать, что приведенное количество теплоты является полным дифференциалом
dS = δQ |
(49) |
T |
|
некоторой функции состояния S. Функция состояния S называется энтропией. Из определения (49) следует, что если у системы в начальном состоянии
{р1,V1,Т1} была энтропия S1, то при переходе в другое состояние при равновесном процессе ее энтропия будет равна:
2 |
δQ |
T2 |
Cпроцесса |
× dT |
|
|
S2 = S1 + ∫ |
|
= S1 + ∫ |
|
|
. |
(50) |
T |
T |
|
||||
1 |
T |
|
|
|
||
|
|
1 |
|
|
|
|
Пример
Определить изменение энтропии 200г воды, охлаждаемой от t1=18˚C до t2=0˚C.
T2 |
dQ |
T2 |
cmδT |
|
T |
|
273 |
|
|
DS = ∫ |
|
= ∫ |
|
= c × m ln |
2 |
= 4190 × 0,2 ln |
|
|
@ = -54 Дж / К . |
T |
T |
T |
291 |
||||||
T |
|
T |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Рассмотрим некоторые свойства энтропии, следующие из определения.
∙Энтропия нескольких тел равна сумме энтропий этих тел:
S= ∑iN=1 Si .
∙При равновесных процессах без передачи тепла (адиабатических процессах) энтропия системы не меняется.
S=const, если Q=0.
∙Энтропия, как и все функции состояния, определяется с точностью до константы, поэтому измеримой величиной является только разность энтропий в начальном и конечном состояниях.
∙При постоянном объеме энтропия является функцией внутренней
энергии |
тела. |
Действительно, согласно |
первому началу |
термодинамики: если dV=0, то δQ=dU, следовательно |
|
||
4 Для доказательства используем общее выражение для КПД тепловой машины, приравняв, его КПД цикла Карно:
|
|
1 - |
Q2 |
= 1 - |
T2 |
|
|
|
||||
|
|
Q1 |
|
|
||||||||
|
|
|
|
|
|
T1 |
||||||
что означает |
|
|
|
|
|
|
|
|
|
|
|
|
|
Q2 |
= |
T2 |
или |
Q2 |
|
= |
Q1 |
. |
|||
|
|
|
|
|
|
|||||||
|
Q1 |
|
T1 |
|
T2 |
|
|
|
T1 |
|||

81
dS = dU . T
Выразим значения энтропии идеального газа через термодинамические
параметры, воспользовавшись уравнениями |
состояния, выражением для |
|||||||||||
внутренней энергии и первым началом термодинамики: |
||||||||||||
δQ = dU + pdV ; p = |
m |
|
RT |
|
; dU = |
m |
C dT ; |
|||||
|
|
|
|
|||||||||
|
|
|
μ |
|
|
V |
|
|
μ |
υ |
||
dS = δQ = |
|
|
|
|
|
|
|
|||||
m |
(C |
|
|
dT |
+ R |
dV |
) . |
|
||||
μ |
|
|
|
|
||||||||
T |
|
υ T |
V |
|
||||||||
После интегрирования получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
m |
υ |
|
S = |
|
dS = |
(C ln T + R lnV )+ const . |
(51) |
|
|
μ |
||||
|
|
|
|
|
|
Это выражение позволяет найти изменение энтропии |
S при каком-либо |
||||
процессев идеальном газе. Используя уравнение состояния идеального газа и уравнение Майера (Cр-Cυ=R), можно выразить энтропию газа через давление p, что в некоторых случаях более удобно:
S = mμ (C p ln T + R ln p)+ const .
Энтропия изолированной системы. Энтропия изолированной системы при обратимых процессах остается постоянной.
Действительно, тепловая машина с нагревателем и холодильником (в частности, машина Карно) составляет изолированную систему. Энтропия системы равна сумме энтропий нагревателя Sн, газа Sг и холодильника Sx. Если передача тепла от нагревателя газу происходит при одинаковой температуре газа и нагревателя T1, то процесс теплопередачи является обратимым. То же самое справедливо для передачи тепла от газа холодильнику, имеющему температуру T2. В процессе передачи тепла Q1 газу имеем:
Sн |
= − |
Q1 |
, |
Sг |
= |
Q1 |
, S∑ = Sh + S г = 0 , |
|
|
||||||
|
|
T1 |
|
|
T1 |
||
и температура системы не меняется. Аналогичные рассуждения приводят к выводу об отсутствии изменения энтропии системы при передаче теплоты Q2 от газа холодильнику при температуре T2.
Рассмотрим теперь необратимый процесс теплопередачи в изолированной системе. Пусть два равных количества идеального газа с температурами T1 и T2 (T1<T2), содержатся в изолированных одинаковых сосудах с жесткими стенками. Если создать тепловой контакт между этими сосудами, то через некоторое время газы в сосудах придут в термодинамическое равновесие, их температуры сравняются и будут равны T=(T1+T2)/2 (из равенства количества теплоты, получаемого первым газом и отдаваемого вторым газом: Cгаза (T- T1)=Cгаза(T2-T)). Согласно (51), энтропия первого газа (объем газа не меняется) возрастет на:
S |
|
= |
m |
C ln |
T |
= |
m |
C ln |
T1 + T2 |
, |
1 |
|
|
|
|
||||||
|
|
μ |
υ |
T1 μ |
υ |
2T1 |
|
|||
|
|
|
|
|
|
|||||
а второго газа изменится на:

82
S |
|
= |
m |
C ln |
T |
= |
m |
C ln |
T1 + T2 |
. |
2 |
|
|
|
|
||||||
|
|
μ |
υ |
T2 μ |
υ |
2T2 |
||||
|
|
|
|
|
||||||
Изменение энтропии этой изолированной системы двух газов при таком процессе равно:
|
|
= |
m |
|
|
T + T |
S |
∑ |
|
C |
ln |
1 2 |
|
|
|
|||||
|
|
μ |
υ |
2T1 |
||
|
|
|
|
|
||
+ ln T1 + T2 2T2
|
= |
m |
|
(T + T )2 |
|
|
|
|
Cυ ln |
1 |
2 |
, |
|
|
|
|
||||
|
μ |
4T1T2 |
||||
|
|
|
|
|||
а, поскольку (Т1+Т2)>4T1T2, логарифм имеет значение, следовательно, SΣ>0.
Таким образом, энтропия любой изолированной системы не может убывать; она либо возрастает, либо остается постоянной.
Это утверждение является еще одной формулировкой второго начала термодинамики, который иногда называют законом возрастания энтропии.
Удобство понятия энтропии состоит в том, что с ее помощью можно определить возможность или невозможность самопроизвольного протекания процессов. Процессы, приводящие к убыванию, энтропии сами по себе (в изолированной системе) протекать не могут. Например, невозможен процесс, обратный только что рассмотренному процессу выравнивания температуры в двух объемах газа. При обратном процессе будем иметь: SΣ<0.
Понятие энтропии тесно связано с понятием количества информации или степенью упорядоченности системы. А именно - чем больше энтропия системы, тем менее она упорядочена. Если газ, помещенный в сосуд, занимает только половину предоставленного объема, такое состояние более упорядоченно, чем состояние с равномерным распределением молекул по всему объему. Из повседневной практики ясно, что сам по себе газ не может собраться в половинке сосуда. Следовательно, закон возрастания энтропии эквивалентен утверждению, что всякая система стремится к состоянию наибольшего хаоса. Обратные процессы от хаоса к упорядоченности в изолированных системах протекать не могут.
2.3.Реальные газы. Фазовый переход жидкость ÷ газ*
Как отмечалось ранее, кинетическая теория идеального газа не учитывает сил взаимодействия молекул, сами же молекулы принимаются за точки. Такая модель соответствует достаточно разреженному газу, подчиняющемуся законам Бойля -Мариотта и Гей-Люссака.
Многочисленные опыты показали, что все газовые законы и, в частности, формула Клайперона - Менделеева носят приближенный характер. Чем сильнее сжат газ, тем заметнее его отклонение от газовых законов. Для того, чтобы можно было применить формулу Клайперона - Менделеева к реальным газам, очевидно, необходимо ввести в нее какие-то поправки. Одно из наиболее удачных уточнений этой формулы предложил в 1983 г. голландский физик Ван- дер-Ваальс.
Первое уточнение Ван-Дер-Ваальса касается объема самих молекул. В 1см3
83
газа при нормальных условиях содержится 2,7 1019 молекул. Принимая эффективный диаметр молекулы равным 3·10-8см, определяем, что ее объем равен 1,2·10-23см3. Находим, что объем всех молекул, находяхщихся в 1см3 газа при нормальных условиях, составляет около 3·10-4см3. Однако при давлении 2500 атм объем самих молекул уже составит половину всего объема газа. Поэтому при высоких давлениях объем газа, занимаемый самими молекулами, необходимо учитывать.
Так как при сжатии газа уменьшается обратно пропорционально давлению не весь объем, а объем свободного пространства между молекулами, в формуле Клайперона - Менделеева вместо V следует ввести (V-b), где b – объем несжимаемой части газа. По вычислению Ван-Дер-Ваальса, b приблизительно равно учетверенному объему всех молекул. Поясним, как получается такой результат.
Действительно, центры молекул не смогут сблизиться больше, чем на расстояние, равное удвоенному эффективному радиусу (2r), т.е. проникнуть в пространство, соответствующее объему шара радиуса 2r (см. рис. 13). Объем
такого шара равен |
|
4 |
π (2r)3 |
= 8 |
4 |
πr 3 , |
т.е. восьмикратному объему одной |
||
3 |
|
||||||||
|
|
|
|
3 |
|
|
|||
молекулы (V0= |
4 |
πк3 ) |
Следовательно, |
каждой из двух выделенных молекул |
|||||
|
|||||||||
3 |
|
|
|
|
|
|
|
|
|
соответствует объем несжимаемого пространства, равный учетверенному объему одной молекулы (4V0).
|
′ |
|
a |
|
|
p |
= V 2 |
, |
|||
|
|||||
2·r
r 
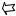 r
r 
Рис. 13. Объем пространства, недоступный центрам двух молекул в процессе их соударения (штрихованная линия)
Вводя указанные поправки, получим формулу
|
|
84 |
|
|
|
|
|
a |
|
|
|
|
|
p + |
(V |
μ |
− b) = RT , |
(52) |
||
|
||||||
|
2 |
|
|
|
||
|
Vμ |
|
|
|
|
называемую уравнением Ван-Дер-Ваальса и записанную для массы газа, равной одному молю (Vµ - объем одного моля газа). Значения коэффициентов a и b приводятся в справочниках также для 1 моля газа. Если масса m газа содержит ν=m/µ молей, то объем газа при прочих равных условиях увеличится в ν раз, т.е. V=νVµ или Vµ=V/ν. Заменив молярный объем Vµ в формуле (52) при помощи полученного соотношения, получим уравнение Ван-дер-Ваальса для любой массы газа:
|
ν 2 a |
|
||
|
|
2 |
|
(53) |
p + |
V |
(V −νb) = νRT . |
||
|
|
|
|
|
Как мы уже отмечали, формула Клайперона - Менделеева хорошо описывает поведение достаточно разреженных газов. В табл. 1 приведены опытные данные для массы азота, занимающей при нормальных условиях объем, равный одному литру. Во втором столбце таблицы приведены значения произведения p V при разных давлениях и одной и той же температуре 0˚C. Это произведение согласно уравнению Клайперона - Менделеева должно оставаться постоянным, а отличие его от единицы указывает на отклонение поведения реального газа от идеального. Как видим, сколько-нибудь заметные расхождения с уравнением состояния идеального газа возникают при давлениях в сотни атмосфер и с ростом давления становятся существенными. В третьем разделе таблицы приведено при тех же условиях произведение подправленных давления и объема, которое должно оставаться постоянным при фиксированной температуре в соответствии с уравнением Ван-Дер-Ваальса. Как видим из таблицы, уравнение Ван-Дер-Ваальса гораздо лучше согласуется с экспериментом, чем уравнение Клайперона – Менделеева.
|
|
|
|
|
Т а б л и ц а 1 |
Р, атм |
pV, aтм · л |
|
ν 2 a |
||
|
|
|
|
|
|
|
|
|
2 |
||
|
|
p + |
V |
(V −νb), атм · л |
|
|
|
|
|
|
|
1 |
1,000 |
|
|
|
1,000 |
100 |
0,994 |
|
|
|
1,000 |
200 |
1,048 |
|
|
|
1,009 |
500 |
1,390 |
|
|
|
1,014 |
1000 |
2,069 |
|
|
|
0,893 |
Изотермы Эндрюса
Английский физик Эндрюс во второй половине прошлого века произвел ряд исследований свойств паров и построил экспериментальные изотермы. В толстостенный цилиндр под поршнем вводились пары углекислого CO2, давление измерялось при помощи манометра.
При изотермическом уменьшении объема давление возрастало и на графике, соответствующем данному процессу (рис. 14), получался участок
85
изотермы 1-2, приближающийся к гиперболе. Таким образом опыты Эндрюса подтвердили, что ненасыщающие пары подчиняются закону Бойля - Мариотта. Точка 2 соответствует объему V2 и показывает состояние паров CO2, при котором они насыщают пространство. При дальнейшем уменьшении объема в цилиндре часть паров переходит в жидкость, а давление оставшихся над жидкостью паров сохраняется при данной температуре неизменным. На графике получается участок 2-3, соответствующий одновременному существованию вещества в двух фазах (в двух агрегатных состояниях) - жидкой и газообразной.
Точка 3 соответствует объему V3 и показывает такое состояние, когда пар полностью обращается в жидкость. Дальнейшее увеличение давления вызывает сжатие жидкости, а так как жидкости крайне слабо сжимаются, участок изотермы 3-4 представляет почти вертикальную линию, лишь незначительно приближающуюся к оси Y.
На рис. 15. показан ряд таких изотерм, соответствующих одной и той же массе CO2, но построенных для разных температур. Чем выше температура, тем участок 2-3 короче, т.е. разность в объемах насыщающего пара (V2) и полученной из него при полной конденсации жидкости (V3) становится меньше.
При некоторой определенной температуре площадка 2-3 исчезает, на графике возникает точка перегиба K, которая носит название критической точки. Температура, при которой она получается, называется критической температурой (Tк), давление, соответствующее точке K - критическим давлением (pк), а объем, занимаемый при этом молем газа - критическим объемом (Vк). При критической температуре ненасыщающий пар переходит в жидкое состояние, как бы минуя стадию насыщения. Для CO2 критическая температура равна 31˚C, критическое давление около 73 атм.
p |
4 |
|
|
|
2 |
|
3 |
|
|
|
1 |
0 |
V2 |
V |
Рис. 14. Изотерма паров СО2, полученная в экспериментах Эндрюса |
||
|
|
86 |
При температурах выше критической вещество может существовать |
||
только в газообразном состоянии и ни при каком давлении не обращается в |
||
жидкость. |
|
|
р |
|
|
рк |
К |
|
|
Жидкость+пар |
|
0 |
Vk |
V |
Рис. 15 Изотермы Эндрюса, соответствующие разным температурам |
||
Понятие о критической температуре впервые было введено в науку Д.И. Менделеевым 1861 г. Он отметил, что при повышении температуры силы взаимодействия между молекулами жидкости слабеют, коэффициент поверхностного натяжения жидкости уменьшается, а при некоторой температуре обращается в нуль. Эту температуру Менделеев назвал температурой абсолютного кипения.
В табл. 2 приведены данные о критических температурах, давлениях и объемах для некоторых веществ.
|
|
|
|
Т а б л и ц а 2 |
Критические параметры некоторых веществ |
|
|||
Вещество |
Tk, ˚С |
Pk, атм |
|
Vk, см3/моль |
Вода |
374 |
218 |
|
57,6 |
Хлор |
144 |
76 |
|
124,0 |
Углекислый газ |
31 |
73 |
|
96,0 |
Кислород |
-118 |
51 |
|
74,3 |
Азот |
-147 |
33,5 |
|
90,0 |
Водород |
-240 |
12,80 |
|
65,0 |
Гелий |
-268 |
2,26 |
|
58,0 |
Из этой таблицы, в частности, следует, что при температурах, больших 374˚C, вода не может существовать в жидком состоянии, какое бы давление мы на нее ни оказывали. Для получения сжиженных газов, их следует предварительно охлаждать до температуры ниже критической и установка должна создавать давление порядка pк.

87
Исследование уравнения Ван-Дер-Ваальса
Преобразуем формулу (52), раскрыв скобки и умножив обе части равенства на V2/p:
V 3 + |
aV |
− bV 2 − |
ab |
= |
RTV 2 |
|
, |
|
|||||||
|
|
|
|
||||||||||||
|
p |
|
|
|
|
|
p |
|
|
|
p |
|
|
|
|
далее расположим слагаемые в порядке убывающих степеней V: |
|
||||||||||||||
|
|
|
|
RT |
|
|
a |
|
|
ab |
|
|
|||
V 3 − V |
2 b + |
|
|
+ |
|
|
V − |
|
|
= 0 . |
(54) |
||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
p |
|
|
p |
|
|
||
|
|
|
|
p |
|
|
|
|
|
|
|||||
Полученное выражение является кубическим уравнением относительно объема5.
Зададимся некоторой определенной температурой T и для нее построим график, выражающий связь V и p по формуле (54). Будем давать p, например 1атм, 1, 5, 2, 2,5 атм и.т.д. Подставляя вместо p его значения, будем получать кубическое уравнения с численными коэффициентами (a, b, R - табличные данные, T - заданная температура). Если для V получится один вещественный корень, соответствующий данному p, на графике будет точка с координатами (p,V). Если при решении уравнения окажутся три вещественных корня, данному давлению будут соответствовать три возможных объема (V1, V2, V3) и кривая, изображающая графически уравнение (54), очевидно, будет иметь перегибы. В результате изотерма Ван-Дер-Ваальса примет вид, изображенный на рис. (16). Ее участок 1-2 соответствует такому же участку, полученному экспериментальным путем на изотерме Эндрюса. Это состояние ненасыщающего пара. Участок 2-3 на опыте получается в виде прямой, на изотерме же Ван-дер-Ваальса - кривая 2-2'-3'-3. Несовпадение этого участка графика с опытными данными не является неожиданным, так как он соответствует состоянию насыщающего пара, для которого формула Клайперона - Менделеева неприменима (уравнение Ван-дер-Ваальса есть подправленная форма уравнения состояния идеального газа). Однако участки 2- 2' и 3-3' при известных условиях могут быть получены на опыте и только участок 2'-3' экспериментально неосуществим. Если осторожно сжимать сначала ненасыщенный пар, а затем после достижения его насыщения (точка 2) продолжать сжатие, при отсутствии в нем ионов и пылинок, которые являются центрами конденсации, можно получить участок 2-2', соответствующий пресыщающему пару. Его давление не может превысить p1; достигнув его, пресыщающий пар начинает бурно конденсироваться, давление падает до pн и дальше (до точки 3) не изменяется. Если постепенно уменьшать давление на сжатую жидкость и продолжать осторожно приподнимать поршень в цилиндре, достигнув при этом давления, соответствующего точке 3', то можно несколько
5 Кубическое уравнение имеет три корня. Поскольку коэффициенты уравнения действительны, один корень всегда будет действительным, а два других, в зависимости от значения коэффициентов уравнения, будут либо действительными, либо комплексно сопряженными. Поскольку объем – действительная величина, в последнем случае будет иметься только один корень, обладающий физическим смыслом.

88
перегреть или <<растянуть>> жидкость и получить экспериментально участок изотермы 3'-3. При достижении газом точки 3' поршень отрывается от жидкости, давление от значения p2 возрастает до значения pн вследствие интенсивного парообразования. Участок 3-4 характеризует жидкую фазу.
\
p |
4 |
|
|
|
|
2΄ |
|
|
|
|
2 |
|
3 |
|
|
|
3΄ |
|
|
|
p2 |
p1 |
pн |
|
|
|
1 |
0 |
|
|
V |
|
|
Рис. 16. Изотерма Ван-Дер-Ваальса |
|
р |
|
|
рк |
К |
|
0 |
Vk |
V |
Рис. 17. Изотермы Ван-Дер-Ваальса, соответствующие температурам, близким к |
||
|
|
критической |
На рис. (17) показан ряд изотерм Ван-дер-Ваальса, построенных для различных температур. Изотерма Tк соответствует критической температуре. Изотермы, расположенные выше нее (для более высоких температур), характеризуются тем, что вещество при этих температурах остается в газообразном состоянии и ни при каком давлении не может быть обращено в жидкость. Для точки K можно найти значение Vк, подставив в уравнение (55)
89
значения критического давления pк и критической температуры T. В этом случае формула принимает вид:
V 3 − V 2 b +
RT V 2 |
|
+ |
a |
k |
|
|
|
|
|
||
pk |
|
|
pk |
|
|
V − |
ab |
= 0 . |
(56) |
|
|||
|
pk |
|
|
С другой стороны, любое кубическое уравнение, имеющие корни V1, V2, V3, можно записать в виде:
(V-V1)(V-V2)(V-V3)=0. |
(57) |
Но для точки K все три корня сливаются в один, т.е. V1=V2=V3=Vк и
последнее соотношение принимает вид:
(V-Vk)3=0.
Раскрывая скобки, его можно привести к виду:
V3-3VkV2+3VkV-Vk3=0. (58)
Так как уравнения (56) и (57) являются тождественными, их коэффициенты при одинаковых степенях неизвестных должны быть равны. Поэтому можно записать:
b + |
RTk |
= 3Vk ; |
a |
= 3Vk = 3Vk2 ; |
ab |
= Vk3 . |
(59) |
|
|
|
|||||
|
pk |
pk |
pk |
|
|||
Эти уравнения связывают между собой шесть величин. Зная три из них, остальные три можно найти. Например, можно теоретически подсчитать критические параметры Vк, pк, Tк по известным a, b, R. И, наоборот, зная Vк, pк, Tк, можно найти постоянные Ван-дер-Ваальса a и b:
b = |
Vk |
, a = 3Vk2 pk . |
(60) |
|
|||
3 |
|
|
|
Характерно, что критический объем оказывается равным утроенной постоянной b. Однако эти соотношения являются приближенными. В некоторых таблицах критических параметров значение критического объема не приводится. Поэтому приведем выражение параметров Ван-Дер-Ваальса a и b через pк, Tк:
|
|
b = |
RT |
27R 2T 2 |
|
|||
|
|
k |
, a = |
|
k |
. |
(61) |
|
|
|
|
8 pk |
64 pk |
|
|||
|
|
|
|
|
|
|
|
Т а б л и ц а 3 |
Удельная теплота парообразования воды при разных температурах |
||||||||
t, ˚C |
0 |
|
50 |
|
100 |
200 |
||
r, М Дж/кг |
2,49 |
|
2,38 |
|
2,26 |
1,94 |
||
Предлагаем вам получить эти выражения из (59) самостоятельно.
Переход жидкости в пар
Переход жидкости в парообразное состояние возможен двумя путями: ∙ посредством испарения;
