
8258
.pdf
Лекция № 15
Элементы корреляционного анализа
Две случайные величины X и Y могут быть независимыми между собой, зависимыми строго функционально Y = ϕ( X ) или зависимыми статистически. При статистической зависимости между случайными величинами распределение одной из величин зависит от того, какое значение имеет другая случайная
величина. Степень статистической зависимости величин |
X и Y характеризует |
||||||
теоретический коэффициент корреляции Пирсона |
|
||||||
|
rXY = |
M ( X × |
Y ) - M ( X ) × |
M (Y ) |
, |
|
|
|
|
|
|
|
|
||
|
|
|
|||||
|
|
|
D( X ) × D(Y ) |
|
|||
обладающий следующими свойствами: |
|
|
|
|
|||
1) |
его значение по модулю не превышает единицы |
− 1 ≤ ρ ХУ ≤ 1. |
|||||
2) |
для независимых величин X и Y |
ρ ХУ = 0 , |
|
||||
3) |
для линейно зависимых величин |
ρ ХУ = ±1 . |
|
||||
Сама статистическая зависимость описывается функциями условного распределения, например, для непрерывных случайных величин функциями
плотности условного распределения f X (x y) или f y ( y x) . Однако нахождение
этих функций и их практическое использование |
обычно затруднено и |
малоэффективно. Чаще статистическая зависимость |
рассматривается в более |
простом виде, в виде функциональной зависимости |
числовых характеристик |
одной из величин от значения другой величины. Такая зависимость называется
корреляционной и описывается функциями регрессии Y (x) или |
X ( y) . Так |
ˆ |
ˆ |
например, наиболее часто используется регрессия в форме условного математического ожидания:
х = ∫ = ˆ
M (Y ) yf y ( y x)dy Y (x) .
Ω y
Корреляционная зависимость приближает статистическую зависимость функциональной зависимостью и имеет следующий вид:
= ˆ + ε
Y Y (x) .
Здесь Y - объясняемая переменная, x - значение объясняющей переменной X , а ε - случайная величина ошибки (невязки) корреляции с нулевым математиче-
ским ожиданием М (ε) = 0 при любом значении х. Дисперсия же ошибки D(ε) не нулевая, но при «хорошей» функции регрессии она не должна быть большой, и не должна зависеть от переменной х. Построение таких функций регрессии является задачей регрессионного анализа.
90

Для приближенного построения функции регрессии будем искать наилучшее в определенном, но довольно широком, m-параметрическом классе функций
таким образом, что бы дисперсия ошибки D(ε, θ1 , θ2 ,..θm ) как функция от параметров θk была минимальной. Такое приближение называ-
ется среднеквадратической регрессией в классе U m . Для приближенного построения функции регрессии можно так же воспользоваться данными наблюде-
ний за величинами X и Y, полученными в выборке (хi , yi ) |
объема n. Такие |
|||
оценки для функции регрессии |
ˆ |
U |
m , |
имеют мини- |
у(x) ищутся так же в кассе |
|
|||
мальное суммарное отклонение от наблюдаемых значений yi , строятся методом
наименьших квадратов и называются выборочной среднеквадратической регрессией.
1. Эмпирическая линейная среднеквадратическая регрессия
Линейная регрессия является простейшей регрессионной моделью, согласно которой функция регрессии является линейной 2-х параметрической функцией:
уˆ (x) = а + вх ,
где а, в - неопределенные коэффициенты, которые оценим по наблюдаемым данным. Пусть имеется двухфакторная выборка n наблюдений (хi , yi ) за величинами X и Y , которую будем называть корреляционным полем. Помимо
выборочных |
средних |
значений |
|
|
|
, |
|
|
|
и |
|
выборочных дисперсий |
|||||||||||||||
|
|
х |
у |
||||||||||||||||||||||||
|
Dx |
= σ2x , Dy = σ2y , вычислим так же среднее произведение |
|
|
и выборочный |
||||||||||||||||||||||
|
xy |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
- |
|
× |
|
|
, который является вы- |
||||||||||||
|
|
|
|
|
|
xy |
|||||||||||||||||||||
(эмпирический) коэффициент корреляции r |
= |
|
x |
y |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
s x ×s y |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
борочным аналогом теоретического коэффициента корреляции Пирсона ρ XY . |
|||||||||||||||||||||||||||
|
|
|
Построим коэффициенты а, в |
методом наименьших квадратов. Для это- |
|||||||||||||||||||||||
го найдем такие значения |
а, в , которые минимизируют сумму квадратов от- |
||||||||||||||||||||||||||
клонения yi |
и yˆ i = yˆ (xi ) , то есть |
ошибки ei |
= yi |
− yˆ i |
|||||||||||||||||||||||
|
n |
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ei2 = ∑( yi |
− yˆ i ) 2 = ∑( yi |
− a − bxi |
)2 min . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
i=1 |
i=1 |
i=1 |
|
|
|
a,b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Из необходимых условий минимума найдем искомые значения а, в : |
|||||||||||||||||||||||||||
|
∂ |
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ei2 = −2∑( yi − a − bxi ) = 0 ; |
|
|
= а + вх |
; a = |
|
− вх |
, |
|||||||||||||||||||
|
y |
y |
|||||||||||||||||||||||||
|
∂a |
||||||||||||||||||||||||||
|
i =1 |
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
91
|
∂ |
n |
n |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
xy |
− xy |
|
|||||||||||
|
|
|
|
|
|
|||||||||||||
|
∑ei2 = −2∑( yi − a − bxi )xi = 0 ; |
xy |
= а |
|
|
+ вх2 ; в = |
|
. |
||||||||||
|
x |
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||||
|
∂b i=1 |
i=1 |
|
|
|
|
x 2 − |
|
2 |
|
||||||||
|
|
|
|
|
x |
|||||||||||||
Через выборочный коэффициент корреляции |
rxy , коэффициент в пред- |
|||||||||||||||||
ставим в форме в = r σ y , а уравнение выборочной линейной среднеквадра-
xy σx
тической регрессии имеет одну из следующих форм:
yˆ (x) = а + вх ;
σ y |
|
yˆ (x) − y = rxy σ |
x |
|
|
yˆ (x) = y + в(х − x) ;
(х − |
|
|
|
yˆ (x) − |
|
|
= r |
(x − |
|
) |
|
|
) |
|
y |
x |
|||||||
x |
|
||||||||||
; |
|
|
|
. |
|||||||
|
|
|
|
|
|
xy |
|||||
|
|
|
|
σ y |
σ x |
||||||
2. Свойства линейной регрессии и коэффициента корреляции
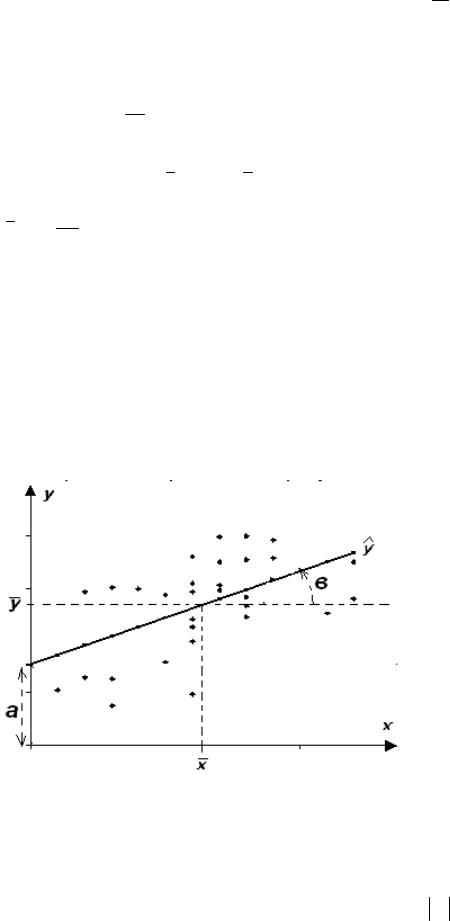
Построенная выборочная линейная среднеквадратичная регрессия является простейшим приближение корреляционной зависимости, показывает тен-
денцию (тренд) этой зависимости |
и изображается прямой на корреляционном |
|||||
поле, наименее уклоняющейся |
от |
его точек. Прямая линия регрессии |
||||
y(x) = а + вх проходит через точку |
(х, у) , отсекает от оси х отрезок а , и |
|||||
ˆ |
|
|
|
|
|
|
имеет угол наклона с тангенсом равным в , как это изображено на рис. 15.1.
Рис. 15.1 Прямая линейной среднеквадратической регрессии
Выборочный коэффициент корреляции rxy характеризует степень кор-
реляционной зависимости наблюдаемых величин Х и У и обладает следующими свойствами:
1) его значения по модулю не превышают единицы ( rxy ≤ 1),
92

2)для независимых Х и У коэффициент близок к нулю(rxy ≈ 0) ,
3)для линейно зависимых величин он близок к единице( rxy »1) .
Геометрически он показывает «тесноту» корреляционного поля возле прямой линии регрессии, что иллюстрирует рис. 15.2 для различных значений коэффициента.
 .
.
Рис. 15.2 Корреляционное поле для различных уровней корреляции величин
Из рис. 15.2 видно, что некоррелированной выборке (rxy ≈ 0) соответст-
вует неориентированное шаровое корреляционное поле, с ростом rxy поле
сжимается и ориентируется к прямой линии регрессии. Знак коэффициента говорит о нарастающем или убывающем тренде зависимости.
|
Ошибки регрессии ei = yi − yˆ i имеют нулевое среднее значение |
|
= 0 , так |
||||||||
|
е |
||||||||||
как |
y = |
|
, |
и минимальную в соответствии с методом наименьших квадратов |
|||||||
y |
|||||||||||
|
|
|
|
ˆ |
|
1 |
n |
||||
|
|
|
|
|
|
|
|||||
дисперсию |
De = |
∑ei2 = Dy (1 − rxy2 ) , так называемую остаточную дисперсию, |
|||||||||
|
|||||||||||
|
|
|
|
|
|
|
n i =1 |
||||
которая тем меньше, чем выше коэффициент корреляции. Величина выборочной дисперсии De является статистической оценкой для дисперсии ошибки D(ε) , однако, это смещенная оценка. Несмещенной (исправленной) оценкой
|
|
|
|
|
|
|
n |
|
|
1 |
n |
|
является величина S 2 = |
De , величина |
S = ( |
∑ei2 )1 / 2 называется стан- |
|||||||||
|
|
|||||||||||
n - 2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
n − 2 i =1 |
|||
дартной ошибкой регрессии. Ошибки для |
коэффициентов регрессии вычис- |
|||||||||||
ляются по формулам: |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Sb2 = |
S 2 |
, Sa2 = |
x 2 ×S 2 |
. |
|
|
|
|
||||
n × Dx |
|
|
|
|
|
|||||||
|
|
|
n × Dx |
|
|
|
|
|||||
В корреляционном анализе также вводится понятие коэффициента детерминации R 2 = DY / DY , показывающего долю объясненной части дисперсии, объяс-
няемой переменной Y. Поскольку D = Dˆ + D , то коэффициент детерминации
y y e
представим так же в следующем виде:
R 2 = 1− De = rxy2 ,
Dy
93

показывающем его прямую связь с коэффициентом корреляции.
Известно [9] распределение случайных величин, связанных с введенными
выше коэффициентами при условии независимости величин |
X и Y : |
||||||
|
rxy |
|
|
|
|
||
n − 2 |
= tn−2 ~ распределение Стьюдента с ν = n − 2 степенями свободы, |
||||||
|
|
|
|
|
|
||
|
1 − r 2 |
||||||
|
|
|
|
xy |
|
|
|
|
R 2 (n − 2) |
= F1,n−2 ~ F-распределение Фишера с ν1 = 1, ν 2 |
= n − 2 степенями |
||||
|
|
|
|
|
|
||
|
1− R |
2 |
|
||||
|
|
|
|
|
|||
свободы.
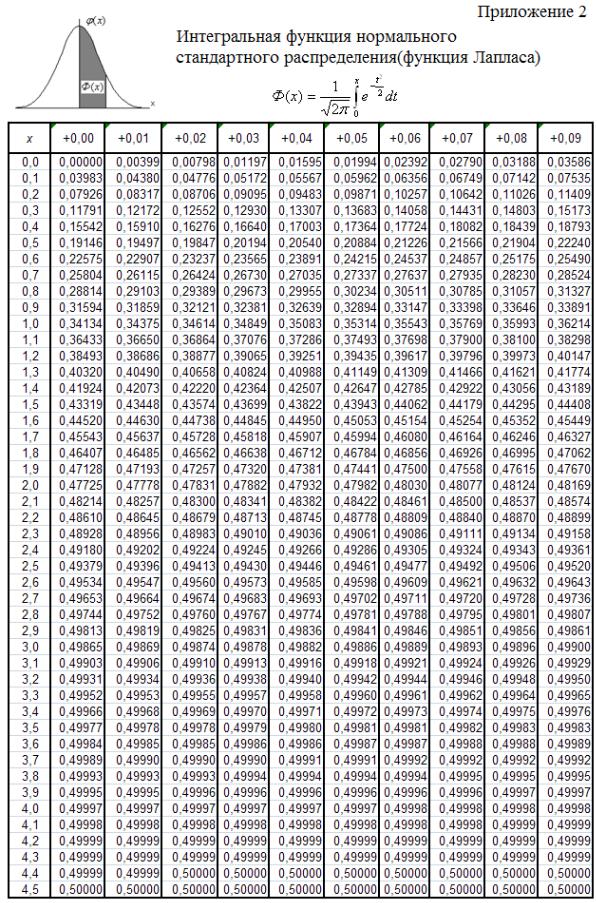
Эти величины используется для построения критериев значимости выборочных коэффициентов rxy и R 2 , и их распределение приводится приложениях 3 и 5 соответственно. Действительно, например, задаваясь уровнем значимости α проверяемой гипотезы H 0 = {ρ XY = 0} , соответствующей независимости величин Х и Y, можно сравнить наблюдаемое значение критерия tnab с крити-
ческим значением tkr (α) . Если tnab < tkr (α) , то гипотеза принимается, что говорит о незначимости выборочного коэффициента корреляции, мало отличного от нуля. Если же tnab > tkr (α) , то гипотеза отвергается, то есть выбороч-
ный коэффициент корреляции, а значит и уравнение регрессии, значимы. Значимость коэффициента корреляции говорит о том, что полученный по данной выборке коэффициент неслучайно отличен от нуля, а корреляционная зависимость между наблюдаемыми величинами существенна.
|
Аналогично |
строится |
критерий |
Фишера для |
проверки гипотезы |
||||||||
H 0 = {R 2 |
= 0} о значимости коэффициента детерминации R 2 : |
||||||||||||
если |
F |
< F (α) , то гипотеза |
H |
0 |
принимается, т.е. R 2 |
незначим. |
|||||||
|
nab |
|
kr |
|
|
|
|
|
|
|
|
||
Выводы критериев значимости rxy |
и R 2 |
идентичны [9]. |
|
||||||||||
|
Значимость коэффициентов регрессии может быть оценена по критериям |
||||||||||||
Стьюдента |
a |
= tn−2 |
, |
|
b |
= tn−2 . |
|
|
|
|
|||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
Sa |
|
|
Sb |
|
|
|
|
|
||
|
3. |
О множественной регрессии |
|
||||||||||
|
На практике, |
|
объясняемая переменная Y часто зависит не от одной, а |
||||||||||
нескольких объясняющих переменных |
Х к . Пусть таких переменных будет |
||||||||||||
m ³1 , и они наблюдаются вместе с переменной Y в многофакторной выборке ( yi x1i , x2i ,..., xmi ) объема n. Построим выборочную линейную регрессию в форме:
94

уˆ (x1 , x2 ,...xm ) = b0 + b1 х1 + b2 x2 + ..... + bm xm + e .
Если введем следующие вектора x = (1, x , x |
|
|
|
|
= (b , b , b |
|
,.....b |
|
)Т |
|
|||||
,...x |
m |
) , b |
2 |
m |
, то |
||||||||||
|
|
1 |
2 |
|
|
|
|
0 1 |
|
|
|
|
|||
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
ее можно записать в векторном виде: |
|
× b . |
|
|
|
|
|
|
|
|
|
||||
y(x) = |
x |
|
|
|
|
|
|
|
|
|
|||||
Введем матрицу |
измерений Х , |
вектор |
|
|
измерения |
y |
и |
|
переменных |
||||||
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
xi = (1, x1i , x2i ,...xmi |
) , а так же вектор регрессии y : |
|
|
|
|
|
|
|
|
|
|||||
1 |
x |
x |
|
x |
|
... |
x |
|
|
|
|
11 |
|
21 |
|
31 |
|
|
m1 |
|
|
1 |
x12 |
x22 |
x32 |
... |
xm 2 |
|
|
|||
Х = |
|
|
|
... |
... |
... |
|
, |
||
... ... ... |
|
|
||||||||
|
x1n |
x2n |
x3n |
... |
|
|
|
|
||
1 |
xmn |
|
||||||||
y1y2
y = ... ,yn
|
x |
|
|
|
i1 |
|
xi 2 |
|
х |
= |
|
i |
... |
|
|
|
|
|
xin |
|
,
y |
|
|
|
|
ˆ |
1 |
|
yˆ |
2 |
|
|
y = |
|
|
, |
ˆ |
|
|
|
... |
|
||
|
|
|
|
yˆ n |
|
||
|
|
|
|
|
ˆ |
|
|
|
|
|
ˆ |
Тогда вектор регрессии будет y |
= X × b , а ошибки регрессии e |
= y |
- y . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Построим |
оценки |
коэффициентов регрессии b методом |
наименьших |
|||||||
квадратов, для чего рассмотрим суммарную ошибку регрессии |
|
|
|
||||||||
n |
|
|
ˆ |
|
ˆ |
|
|
|
|
|
|
2 |
T |
|
T |
T |
|
|
|
||||
|
|
|
|
|
|||||||
∑ ei |
= e |
× e = ( y - y) |
|
× ( y - y) = ( y - X × b ) |
|
× ( y - X × b ) . |
|
|
|
||
i =1
Подберем такие коэффициенты b , при которых суммарная ошибка регрессии минимальна, для этого рассмотрим условие минимума:
¶ |
n |
|
|
||
∑ei2 = -2 × ( X T × y - X T × X × b ) = 0 , в = ( X T × X ) −1 × ( X T × y) . |
||
¶b i =1 |
|
|
Таким образом, оценка для коэффициентов регрессии - построена. Матрица, входящая в выражение для коэффициентов имеет вид средних перекрестных произведений:
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
x1 |
|
|
x1 x1 |
|
|
x1 x2 |
|
|
x1 x3 ... |
|
|
x1 xm |
|
|
|
|
|
|
|
|
|
|
|
|
yx |
|
|
|
||||||||||||||||||||||
|
T |
× X = n × |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= W |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
Х |
x |
|
|
x |
|
x |
|
x |
|
x |
|
|
x |
|
x |
|
... |
|
x |
|
x |
|
|
|
|
X |
T |
|
= n × |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx |
|
|
||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
2 |
2 |
|
2 |
3 |
|
2 |
m |
, |
|
× y |
|
2 |
|
|
. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
... |
|
|
|
... |
|
|
|
|
... |
|
|
|
|
... ... |
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
xm x1 |
|
xm x2 |
|
xm x3 ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
xm |
|
|
|
|
xm xm |
|
|
|
|
|
|
|
|
yxm |
||||||||||||||||||||||||||||||||||||
|
|
Значимость |
|
построенного |
уравнения |
|
линейной |
|
среднеквадратической |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
регрессии |
y(x) = |
x × b |
проверяется по значимости коэффициентов регрессии |
||||||||||||||||||||||||||||||||||||||||||||||||||
bк |
|
или коэффициента детерминации |
R 2 = |
DY |
|
= 1 − |
De |
|
. |
Для проверки вычис- |
|||||||||||||||||||||||||||||||||||||||||||
|
DY |
Dy |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
95 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
1 |
n |
|
1 |
|
n |
ляются: |
De |
= |
∑ ei2 - дисперсия |
ошибок регрессии, S 2 = |
|
× ∑ei2 - не- |
||
|
|
|
||||||
|
|
|
n i =1 |
|
n - m -1 i =1 |
|||
смещенная стандартная ошибка |
регрессии, Sb2 = S 2 ×Wкк−1 |
- несмещенные |
||||||
K
дисперсии коэффициентов регрессии.
Для построения критериев значимости воспользуемся известными статистиками:
bk = tn−m−1
Sbk
~ распределение Стьюдента с ν = n − m − 1степенями свободы,
R 2 |
× |
n - m -1 |
= F |
,ν2 |
~ F-распределение Фишера с ν |
|
= m, ν |
|
= n − m −1 |
1 - R 2 |
m |
|
|
||||||
|
ν1 |
|
1 |
|
2 |
|
степенями свободы. Задаваясь уровнем значимости α проверяемой гипотезы H 0 = {bk = 0} , соответствующей независимости величин Х r и Y , можно сравнить наблюдаемое значение критерия tnab с критическим значением tkr (α) . Если tnab < tkr (α) , то гипотеза принимается, что говорит о незначимости коэффициента bк , мало отличного от нуля, то есть о незначимости переменной
Х r в уравнении регрессии, такие переменные желательно исключить из модели регрессии. Аналогично проверяется гипотеза о значимости коэффициента детерминации H 0 ={R 2 = 0} , соответствующей значимости всего уравнения
регрессии в целом. Сравнивая наблюдаемое значение критерия Fnab , с критическим значением Fkr (α) , можно утверждать, что если Fnab < Fkr (a) , то гипо-
теза принимается, что говорит о незначимости коэффициента R 2 , мало отличного от нуля, то есть о не значимости уравнения регрессии в целом.
Помимо значимости построенного уравнения регрессии, его качество оценивается так же отсутствием зависимости между объясняющими переменными
Х r (мультиколлинеарности), отсутствием зависимости величины дисперсии ошибок De от переменных Х к и Y (гетероскедастичности), отсутствием зависимости ошибок ei = yi − yˆ i между собой (например, автокорреляции).
Мультиколлинеарность приводит к неустойчивости обращения матрицы W, а ее устранение возможно путем исключения из регрессионной модели малозначимых и сильнозависимых объясняющих переменных (факторов). Для такого исключения построим корреляционную матрицу парных коэффициен-
|
|
xi x j |
- |
|
i × |
|
j |
. Тогда, |
|
|
≈ 1 , а коэффициент b |
|
|
тов корреляции: r = |
|
x |
x |
если |
r |
|
незна- |
||||||
|
|
|
|
|
|
|
к |
||||||
ij |
sxi × sx j |
|
iк |
|
|
||||||||
|
|
|
|
|
|
|
|||||||
чим или малозначим, то переменную |
Х к можно исключить из модели регрес- |
||||||||||||
сии, если коэффициент детерминации при этом значимо не уменьшается.
96
Гетероскедастичность и автокорреляция могут быть установлены при помощи теста ранговой корреляции Спирмена и теста Дарбина-Уотсона соответственно [1]. Влияние этих нежелательных для качества регрессии факторов может быть ослаблено путем различного рода преобразования переменных регрессионной модели [9].
3. О нелинейной регрессии
Иногда линейная модель регрессии бывает недостаточной, с точки зрения ее качества и значимости, поэтому может быть использованы нелинейные модели. В простейшей форме нелинейность может быть учтена путем введения
инструментальных переменных zr = ϕr (xk ) , которые входят в модель регрессии обычным линейным образом. При этом часто используются степенная
функция zr |
= x λ , логарифмическая zr = ln x , показательная zr = e x |
и иногда |
||||||||||||||||||
тригонометрическая |
zr |
= Sin(ωx + ϕ0 ) |
для выявления циклических факторов в |
|||||||||||||||||
зависимостях. |
|
Например, |
нелинейная модель 2-го порядка может быть по- |
|||||||||||||||||
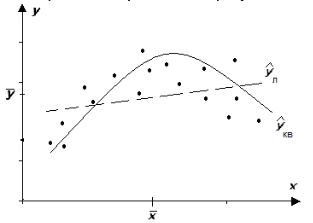
строена следующим образом (рис. 15.3): |
|
|
|
|
|
|||||||||||||||
ˆ |
|
= |
b0 |
+ |
b1 х |
+ |
b2 x |
2 |
+ |
e |
|
уˆ (x, z |
2 |
) = b + b х + b z |
2 |
+ e |
, |
|
||
у(x) |
|
|
|
|
|
|
0 1 |
2 |
|
|
||||||||||
где |
z2 = x 2 |
- инструментальная переменная. Введение новых членов в модель |
||||||||||||||||||
регрессии, |
|
в том числе и инструментальных, оправдано тогда, когда |
значимо |
|||||||||||||||||
повышается коэффициент детерминации. |
|
|
|
|
|
|||||||||||||||
Рис.15.3 Кривая нелинейной среднеквадратической регрессии 2-го порядка.
Иногда |
строится |
|
|
мультипликативная |
модель |
регрессии |
|||
ˆ |
, x2 |
b1 |
× x |
b2 |
bm |
× e , |
которая |
путем логарифмирования |
|
у(x1 |
,...xm ) = b0 × х1 |
2 |
×.... × xm |
||||||
может быть сведена к обычной аддитивной линейной модели для инструментальных переменных.
97

98
99
