
6858
.pdf10
&& |
= Fx |
|
mx |
|
|
&& |
= Fy |
|
my |
|
|
&& |
= Fz . |
(2.2) |
mz |
Дифференциальные уравнения движения материальной точки в естественных осях могут быть получены с помощью формул кинематики, после чего они приобретают следующий вид:
m |
dvτ |
= F |
|
||
|
|
|
|||
|
dt |
τ |
|
||
|
|
|
|||
v2 |
|
|
|||
|
= Fn |
|
|||
m |
|
|
|
||
ρ |
|
||||
|
|
|
|||
|
0 = Fb |
|
|||
|
(2.3) |
||||
|
|
|
. |
||
2.2.ПЕРВАЯ ЗАДАЧА ДИНАМИКИ
Если закон движения задан в векторной форме, выражение для вектора силы могут быть найдены путем дифференцирования радиус-вектора по формулам
(2.1).
Если закон движения задан в аналитической форме, проекции силы на декартовые оси могут быть найдены путем дифференцирования координат по форму-
лам (2.2).
Если закон движения задан в естественной форме, проекции силы на оси естественного трехгранника могут быть найдены путем дифференцирования по
(2.3).
ПРИМЕР |
(кг) в плоскости происходит в соответствии с урав- |
||||
Движение точки массой |
|||||
нениями: |
|
, , |
где С1, С2, С3 - некоторые постоянные |
||
величины. |
|
|
|
|
|
Найти силу, вызывающую это движение. |
|||||
Решение |
|
|
|
|
|
Движение точки задано координатным |
способом, поэтому применим уравнения |
||||
(2.2), учитывая, что: |
; с . |
|
|||
|
|
|
|
м |
|
Тогда ; .

11
Ответ: Действующая сила равна по модулю Н и направлена по осиx .
2.3.ВТОРАЯ ЗАДАЧА ДИНАМИКИ
Вторая задача динамики заключается в определении движения под действием заданных сил. Ее решение сводится к интегрированию дифференциальных уравнений (2.1), (2.2) или (2.3).
Пусть, движение точки описывается в декартовых осях. Тогда система уравне-
ний (2.2)
&& |
|
|
& |
& & |
|
|
|
mx |
= Fx ( x, y, z, x, y, z,t ) |
|
|
|
|||
&& |
|
|
& |
& & |
|
|
|
my |
= Fy ( x, y, z, x, y, z,t ) |
|
|
||||
&& |
|
|
& |
& & |
|
|
|
mz |
= Fz ( x, y, z, x, y, z,t ) |
|
|
|
|||
имеет общее решение в виде |
|
|
|
|
|
|
|
x = x (t, C1 , C2 , C3 , D1 , D2 , D3 ) |
|
||||||
y = y (t, C , C |
, C , D , D , D ) |
|
|||||
|
1 |
2 |
3 |
1 |
2 |
3 |
|
z = z (t, C1 , C2 , C3 |
, D1 , D2 |
, D3 ) |
. |
||||
|
|
|
|
|
|
|
|
При решении задач обычно принимают, что t0 = 0 , а C1, C2 , C3 , D1, D2 , D3 − постоянные интегрирования, которые определяются из начальных условий, описывающих состояние материальной точки в начальный момент времени t = t0 .
В качестве начальных условий задаются начальное положение точки и ее начальная скорость:
x0 = xx&0 = x&
y0 = yy&0 = y&
z0 = zz&0 = z&
t =0
t =0
t =0
t =0
t =0
t =0
Из этих шести уравнений определяются шесть постоянных интегрирования.
ПРИМЕР
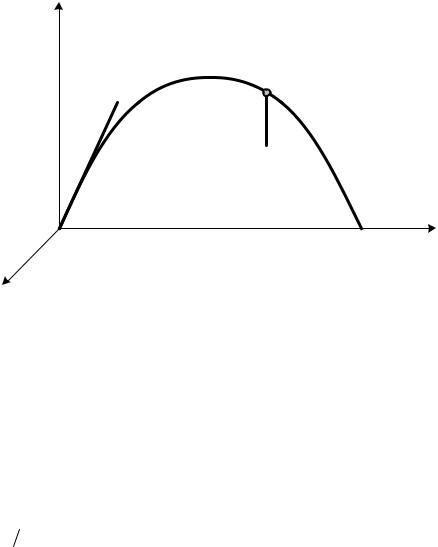
Материальную. точку бросают под углом α к горизонту с начальной скоростьюНайти уравнение движения материальной точки. Сопротивление воздуха и изменение с высотой силы тяжести не учитывать.
12
Решение
Выберем систему отсчета (см. рис. 2.1). Запишем дифференциальные уравнения (2.2):
mx&& = 0
my&& = −mg
mz&& = 0
y
v0 
G = mg 
O
x
z
Рис. 2.1
Интегрируя уравнения, получаем:
& |
= C1 |
x |
|
& |
|
y = −gt + C2 |
|
& |
= C3 |
z |
|
Интегрируя уравнения еще раз, получаем:
x = C1t + D1 |
|
||||
|
|
|
2 |
2 |
+ C2t + D2 |
y = −gt |
|
||||
z = C |
t + D |
|
|||
|
3 |
|
|
3 |
|
(*)
Для определения постоянных интегрирования C1, C2 , C3 , D1, D2 , D3 используем начальные условия:

13
x0 = xx&0 = x&
y0 = yy&0 = y&
z0 = zz&0 = z&
t =0 = 0
t =0 = v0 cosα
t =0= 0
t =0= v0 sin α
t =0 = 0 |
|
t =0 = 0 |
, откуда получаем: |
D1 = 0
C1 = v0 cosα
D2 = 0
C2 = v0 sin α
D3 = 0C3 = 0
Подставляя постоянные интегрирования в уравнения (*), получим:
|
x = (v0 cosα )t |
|
||
|
y = −gt 2 |
2 + (v sin α )t |
||
|
|
|
0 |
|
|
z = 0 |
|
(**) |
|
|
|
|
||
|
Исключим из уравнений (**) время, для чего выразим t из первого урав- |
|||
|
нения: |
|
|
|
|
t = x / (v0 cosα ) |
, |
||
|
|
|
|
|
|
и затем подставим полученное выражение во второе уравнение: |
|||
|
gx2 |
|
|
|
y = − |
|
+ (tg α ) x. |
||
2v2 cos2 α |
||||
|
0 |
|
|
|
В полученное соотношение не входит время. Оно представляет собой уравнение траектории материальной точки.
|
|
|
|
gx2 |
|
Ответ: |
Уравнение траектории точки: |
y = − |
|
|
+ (tg α ) x. |
2v2 |
cos2 α |
||||
|
|
|
0 |
|
|
2.4. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ
Пусть материальная точка движется в положительном направлении оси x .
ax |
= |
dvx |
= |
dv |
|
F = F . |
|
|
|||||
Тогда |
|
dt dt , |
||||
|
|
|
|
|
|
x |
Запишем дифференциальное уравнение движения
mdv = F ( x, v,t ) dt
ирассмотрим способы его интегрирования с учетом начальных условий
x0 = xx& = x&0
t =0
t =0
длятрехчастныхслучаев:

|
14 |
когда сила зависит от времени |
F = F (t ) , |
когда сила зависит от скорости |
F = F (v) , |
когда сила зависит от координаты F = F ( x) .
Частный случай 1, когдасила зависит от времени:
mdv = F (t ) dt .
Умножив обе части уравнения на dt , разделим переменные t и v :
m dv = F (t )dt
При интегрировании уравнения можно пользоваться определенными или неопределенными интегралами.
Используем неопределенные интегралы:
m ∫ dv = ∫ F (t )dt , откуда mv = ∫ F (t )dt + C1 ,
где C1 определяется из начального условия.
Используем определенные интегралы:
v |
t |
m ∫ |
dv = ∫ F (t )dt |
v0 |
0 |
Интегрируя и выполняя подстановку, получим:
t
mv − mv0 = ∫ F (t )dt
0 |
. |
|
При использовании определенных интегралов определение постоянных интегрирования не требуется, так как после взятия интеграла и подстановки величину скорости можно будет выразить непосредственно.
Частный случай 2, когда сила зависит от скорости:
m dv = F (v)
|
dt |
. |
|
|
|
|
|
dt |
|
Умножив обе части равенства на |
|
, получим |
||
F (v) |
||||
m |
dv |
= dt |
||
|
||||
F (v) |
||||

15
Используем неопределенные интегралы:
m |
∫ |
dv |
= |
∫ |
dt |
m |
∫ |
dv |
= t + C |
|
F (v) |
F (v) |
|||||||||
|
|
|
|
1 |
||||||
|
|
|
|
|
, откуда |
|
|
|
, |
где C1 определяется из начального условия.
Используем определенные интегралы:
v |
dv |
t |
|
v |
dv |
|
|
m∫ |
= ∫dt |
|
m∫ |
= t |
|||
F (v) |
|
F (v) |
|||||
v0 |
0 |
или |
v0 |
. |
|||
|
|
После взятия интеграла и подстановки пределов получим выражение для v , не содержащее постоянных интегрирования.
Частный случай 3, когда сила зависит от координаты:
mdv = F ( x) dt .
Выполним замену |
dv |
= |
dv |
× |
dx |
= |
dv |
v , получим уравнение |
|||||
|
|
|
|
||||||||||
|
|
|
dt dx dt |
|
dx |
|
|||||||
mv |
dv |
= F ( x ) |
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||||
|
dx |
. |
|
|
|
|
|
|
|
||||
Умножим обе части уравнения наdx : |
|
||||||||||||
mvdv = F ( x)dx . |
|
|
|
|
|
||||||||
Используем неопределенные интегралы: |
|
||||||||||||
m∫vdv = ∫ F ( x)dx , |
откуда m |
v2 |
= ∫ F ( x)dx + C1 . |
||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|||
ПостояннаяC1 определяется из начального условия.
Используем определенные интегралы:
v |
x |
|
|
|
v |
2 |
2 |
x |
|
m∫ |
vdv = ∫ F ( x)dx |
|
|
m |
|
− m |
v0 |
= ∫ F ( x)dx |
|
|
|
|
|
|
|||||
v0 |
x0 |
, |
откуда |
2 |
2 |
x0 |
|||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
После взятия интеграла и подстановки пределов получим выражение для v , не содержащее постоянных интегрирования.
Примечание

16
Если требуется получить не только выражение скорости v(t ) , но и выражение для координаты точки x(t ) , то описанный процесс интерирования следует повторить.
Тема 3. Теорема о движении центра масс
3.1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
Рассмотрим механическую систему, состоящую из n точек. Положениеk-й точ-
ки определяется радиус-вектором rk . Точка имеет массу mk и движется со ско- |
|
|
R |
ростью vk |
и с ускорением ak . |
R |
R |
Силы, действующие на материальную точку можно разбить на две группы.
Сделать это можно разными способами.
Первый способ
Разделим силы, действующие на k-ю точку,на внешние и внутренние. Получим следующую запись основного уравнения динамики:
R |
= Fke + Fki |
(k = 1, 2,..., n) |
|
ma |
(3.1) |
||
|
|
|
гдеFke (external ) − равнодействующая внешних сил,
Fki (internal ) − равнодействующая сил, действующих со стороны тел системы.
Второй способ
Разделим силы, действующие наk-ю точку, на активные силы и реакции связей. Получим следующую запись:
R |
= Fk |
+ Rk |
(k = 1, 2,..., n) |
|
ma |
(3.2) |
|||
|
|
|
|
где Fk − равнодействующая активных сил, приложенных к точке k ,
Rk − равнодействующая реакций связей, действующих на точку k.
При этом выполнится равенство |
Fe + Fi = F + R . |
|
k k k k |
||
|
Первый способ записи основного уравнения используется при решении задач динамики с помощью основных теорем динамики, которые включают в себя:
17
теорему о движении центра масс, теорему об изменении количества движения,
теорему об изменении кинетического момента, теоремы об изменении кинетической энергии.
Второй способ записи основного уравнения применяется при решении задач динамики методамианалитической механики, которые включают в себя:
принципЛагранжа, принципд’Аламбера,
принципд’Аламбера − Лагранжа, уравненияЛагранжавторогорода.
3.2. ЦЕНТР МАСС МЕХАНИЧЕСКОЙ СИСТЕМЫ
Массой механической системы называется сумма масс ее точек:
n
m = ∑ mk
k =1 |
. |
(3.3) |
Центром масс механической системы называется геометрическая точка С, ра- диус-вектор которой определяется по формуле:
R |
|
1 |
n |
R |
rC |
= |
|
∑ mk rk |
|
|
||||
|
|
m k =1 |
(3.4) |
|
Проектируя последнее равенство на оси, получим формулы для координат центра масс, которые аналогичны формулам для определения координат центра тяжести:
|
|
1 |
n |
|
|
|
1 |
n |
|
|
|
1 |
n |
|
xC |
= |
∑ mk xk |
|
yC |
= |
∑ mk yk |
|
zC |
= |
∑mk zk |
|
|||
|
, |
|
, |
|
(3.5) |
|||||||||
|
|
m k =1 |
|
|
m k =1 |
|
|
m k =1 |
||||||
Центр масс иногда называют центром инерции.
Центр масс более общее понятие, чем центр тяжести, поскольку сохраняет смысл даже при отсутствии сил тяжести.
Если массы материальных точек постоянны, то дифференцированием уравне-
ния (3.4)
получим выражение для скорости центра масс
R |
|
1 |
n |
R |
|
vC |
= |
|
∑ mk vk |
(3.6) |
|
|
|||||
|
|
m k =1 |
, |
||
и выражение для ускорения центра масс системы:
|
|
|
|
18 |
R |
|
1 |
n |
R |
aC |
= |
|
∑ mk ak |
|
|
||||
|
|
m k =1 |
(3.7) |
|
3.3. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС МЕХАНИЧЕСКОЙ СИСТЕМЫ
ТЕОРЕМА
Произведение массы системы на ускорение центра масс равно главному вектору внешних сил, действующих на точки системы:
R |
n |
R |
|
= ∑ Fke |
|||
maC |
|||
|
k =1 |
(3.8) |
|
или в проекциях на оси
|
|
n |
|
&& |
e |
|
|
mxC |
= ∑Fkx |
|
|
|
|
k =1 |
|
|
|
n |
|
&& |
e |
|
|
myC |
= ∑Fky |
|
|
|
|
k =1 |
|
|
|
n |
|
|
&& |
e |
|
mzC |
= ∑Fkz |
(3.9) |
|
|
|
k =1 |
|
Доказательство
Просуммируем все дифференциальные уравнения движения механической системы (3.1), в результате чего получим
n |
R |
n R |
n R |
|
= ∑ Fke + ∑ Fki |
||
∑ mk ak |
|||
k =1 |
|
k =1 |
k =1 . |
Если учесть, что силы взаимодействия внутри системы попарно равны и противоположно направлены, получим, что главный вектор внутренних сил равен нулю:
n |
R |
∑ Fki = 0 |
|
k =1 |
. |
n
Кроме того, по формуле (3.7) имеем ∑ R = R .
mk ak maC
k =1
Отсюда следует справедливость уравнений (3.8), которые называются дифференциальными уравнениями поступательного движения твердого тела.
Теорема доказана

19
Другими словами, центр масс механической системы движется как материальная точка, в которой сосредоточена вся масса системы и к которой приложены все внешние силы, действующие на систему.
Вывод: внутренние силы не могут изменить движение центра масс.
3.4. СОХРАНЕНИЕ ДВИЖЕНИЯ ЦЕНТРА МАСС (СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ)
Следствие 1
Если главный вектор внешних сил механической системы все время равен нулю, то центр масс системы находится в покое или движется равномерно и прямолинейно.
n R |
, то из (3.8) |
R |
R |
= const . |
Действительно, если ∑ Fke = 0 |
получаем, что aC |
= 0 , откуда vC |
k =1
Следствие 2
Если сумма проекций всех внешних сил на какую-либо ось все время равна нулю, то проекция скорости центра масс на эту ось постоянна.
n |
|
Действительно, если ∑ Fkx = 0 , то из (3.9) получаем, что xC = 0 . |
|
e |
&& |
|
|
k =1 |
|
Отсюда следует, что xC = const |
( центр масс движется по оси x равномерно или |
& |
|
покоится: vCx = const ).
Тема 4. Теорема об изменении количества движения
4.1. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
Количеством движения материальной точки называется векторная величина,
равная произведению массы точки на ее скорость: = R .
Q mv
Количеством движения материальной системы называется векторная сумма количеств движения всех точек системы:
R n |
R |
|
Q = ∑ mr vr |
(4.1) |
|
r =1 |
. |
|
