6822
.pdf
60
Подставляя в дифференциальные уравнения движения материальной точки в координатной форме найдем:
Fx = m&x& = −mω2 x,
Fy = m&y& = −mω2 y,
F = |F| = 
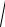Fx2 + Fy2 = mω2r.
Ответ: F = mω2r.
Задача 3.2. Первая задача динамики
Точка массы m кг движется прямолинейно по закону S = πt 2 ( S - в метрах, t - в секундах). Найти силу, под действием которой движется точка.
Решение Находим проекции искомой силы на естественные оси.
2
Pτ = m d S2 = m2π dt
2
Pn = m Vρ = 0 (радиус кривизны прямой ρ = ∞ )
Рb = 0
P = 
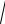Pτ2 + Pn2 + Pb2 =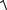 
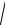(2πт)2 + 0 + 0 = 2πm . Ответ: Р=2πт.
Задача 3.3. Вторая задача динамики Материальную точку бросают под углом α к горизонту с начальной скоростью
'›. Найти уравнение движения материальной точки. Сопротивление воздуха и изменение с высотой силы тяжести не учитывать.
61
y
v0
G = mg
O
x
z
Рис. 3.1
Решение:
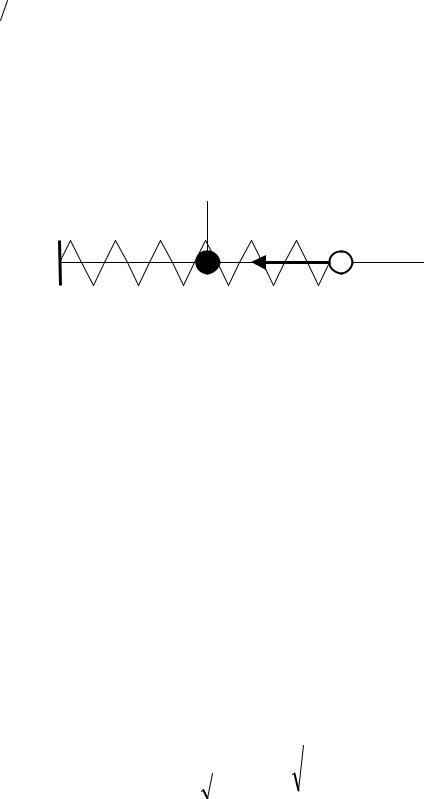
1.Выберем систему отсчета (рис. 3.1).
2.Запишем дифференциальные уравнения движения материальной точки в координатной форме:
mx&& = 0
my&& = −mg
mz&& = 0
3. Интегрируя уравнения, получаем:
& |
= C1 |
x |
|
& |
|
y = −gt + C2 |
|
& |
= C3 |
z |
|
4. Интегрируя уравнения еще раз, получаем:
x = C1t + D1 |
|
|||
|
|
2 |
2 |
+ C2t + D2 |
y = − gt |
|
|||
z = C t + D |
|
|||
|
3 |
|
3 |
|
5.Для определения постоянных интегрирования C1, C2 , C3 , D1, D2 , D3 используем начальные условия:
x0 = xx&0 = x&
y0 = yy&0 = y&
z0 = zz&0 = z&
t =0= 0
t =0= v0 cosα
t =0= 0
t =0= v0 sin α
t =0= 0 |
|
|
t =0 |
= 0 |
, откуда получаем: |
|
|
|
D1 = 0
C1 = v0 cosα
D2 = 0
C2 = v0 sinα
D3 = 0C3 = 0
6. Подставляя постоянные интегрирования в уравнения получим:
62
x = (v0 cosα ) t |
|
|
+ (v0 sin α )t |
y = −gt 2 2 |
|
|
|
z = 0 |
- закон движения материальной точки |
|
|
Задача 3.4. Вторая задача динамики
Найти закон движения точки массой m , упруго закрепленной на пружинке с жесткостью c , при начальных условиях: x(0) = a , x&(0) = 0.
y
O
x
F = – cr
Рис. 3.2
Решение:
Движение точки происходит под действием упругой силы пружины, направленной к положению равновесия и равной F = – cr ( рис. 3.2).
Проектируя основное уравнение динамики ma = – cr на ось Ox , вдоль которой происходит движение, и выбирая начало отсчета на конце недеформированной пружины, получим дифференциальное уравнение движения точки:
ma = – cx .
Воспользовавшись второй подстановкой и умножив обе части уравнения на dx , найдем первый интеграл:
v |
|
|
|
|
x |
|
|
||
∫vdv = −(c / m)∫ xdx |
|||||||||
0 |
|
|
|
|
|
a |
|
|
|
или v2/2 = – ( с/m)(x2/2 – x 02/2), откуда |
|
|
v = (с/m)(x02 – x 2). |
||||||
Подставляя v = dx/dt и разделяя переменные, получим: |
|||||||||
x |
|
|
|
|
|
|
|
t |
|
dx |
|
|
|
|
c |
|
|||
∫ |
|
|
= |
|
|
|
∫ dt , |
||
|
|
|
|
|
|
||||
x 2 − x 2 |
|
|
m |
||||||
x =a |
|
|
|
|
0 |
||||
0 |
|
0 |
|
|
|
|
|
|
|
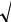
63
|
x |
|
x |
|||
|
|
|||||
|
|
|
|
|
||
arc sin |
|
= (c / m) ·t, |
||||
|
|
|||||
x0 |
||||||
|
|
x |
||||
|
|
0 |
|
|
||
arc sin(x/x0) – π/2 = "с/•$ ·t,
откуда x = a sin(ωt + π/2) = a cos ωt ,
где a = x0, ω = "с/•$
Ответ: x = a sin(ωt + π/2) = a cos ωt , где a = x0, ω = "с/•$.
3.2 ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС МЕХАНИЧЕСКОЙ СИСТЕМЫ
Произведение массы системы на ускорение центра масс равно главному вектору
внешних сил, действующих на точки системы:
|
|
|
n |
|
&& |
e |
|
|
mxC |
= ∑ Fkx |
|
|
|
|
k =1 |
|
|
|
e |
|
|
|
n |
или в проекциях на оси |
my&&C |
= ∑ Fky |
|
|
|
|
k =1 |
|
|
|
n |
|
|
&& |
e |
|
mzC |
= ∑ Fkz |
|
|
|
|
k =1 |
R |
n R |
|
= ∑ Fke |
||
maC |
||
|
k =1 |
Другими словами, центр масс механической системы движется как материальная точка, в которой сосредоточена вся масса системы и к которой приложены все внешние силы, действующие на систему. Внутренние силы не могут изменить движение центра масс.
Следствие 1:
Если главный вектор внешних сил механической системы все время равен нулю, то центр масс системы находится в покое или движется равномерно и прямолинейно.
Следствие 2:
Если сумма проекций всех внешних сил на какую-либо ось все время равна нулю, то проекция скорости центра масс на эту ось постоянна.
Задача 3.5. Теорема о движении центра масс На неподвижную однородную призму А, лежащую на горизонтальной плоскости,
положили однородную призму В. Ширина основания призмы А равна a=10 м. Ширина основания призмы В равна b=2 м. Пренебрегая трением, определить смещение
64
призмы А после того, как призма В опустится по призме А. Принять, что масса призмы В втрое меньше массы призмы А.
y
|
|
a |
|
|
|
b |
|
|
|
B |
|
|
A |
|
|
O |
P |
P2 |
x |
1 |
|
|
|
|
x1 |
|
|
|
x2 |
|
|
|
|
Рис.3.3 |
|
Решение: |
|
|
|
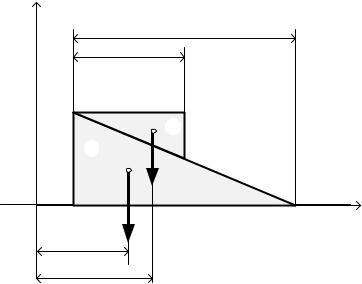
Введем неподвижную систему координат Оху. В этой системе координат обозначим за х1 и х2 координаты центров масс призм А и В в начальный момент времени (рис. 3.3). Смещение по горизонтали, призмы А обозначим S.
Смещение в процессе движения верхней призмы В относительно нижней призмы А будет равно (a-b). Тогда смещение верхней призмы относительно неподвижной системы координат составит S+(a-b).
В конечный момент времени координаты центров масс призм А и В будут соответственно равны
x1′ = x1 + S, x2′ = x2 + S +(a −b).
Механическая система состоит из двух тел: однородных призм А и В. Внешними силами, приложенными к системе являются силы тяжести: Р1 и Р2 и реакция гладкой поверхности основания призмы А, направленная по вертикали (на рисунке не показана). Все эти внешние силы вертикальны, поэтому сумма их проекций на горизонтальную ось равна нулю.
В соответствии со следствием 2 из теоремы о движении центра масс делаем вы-
|
n |
вод: поскольку сумма проекций внешних сил на ось х равна нулю , то ∑Fkxe = 0 , то |
|
|
k =1 |
& |
= const. |
xC |
|
Поскольку в начальном состоянии система покоится, то хс=const.
65
Запишем выражение для определения положения центра масс в начальном поло- |
|
жении системы: 1с |
3zžzY3/ž/ |
žzYž/ |
|
Запишем выражение для определения положения центра масс в конечном поло-
жении системы с учетом изменения начальных координат точек приложения сил Р1 |
|||
и Р2: 1с |
3ŸzžzY3Ÿ/ž/ |
|
"3zY $žzY"3/Y Y"¡k¢$$ž/ |
žzYž/ |
žzYž/ |
||
Так как знаменатели в этих выражениях равны, то приравняем числители дробей:
1C•C 15•5 "1C £$•C "15 £ "- ¤$$•5
Упрощая |
|
|
полученное |
равенство, |
получим: |
|||
"•C •5 |
$£ "- ¤$•5 0 |
|
|
|||||
Решая полученное уравнение относительно неизвестной переменной S, полу- |
||||||||
чим £ |
kž/"¡k¢$ |
|
ž/"C›k5$ |
2м |
|
|
||
|
žzYž/ |
¥ž/ |
|
|
|
|||
Ответ: |
S = 2м, влево. |
|
|
|
|
|||
Задача 3.6. Теорема о движении центра масс
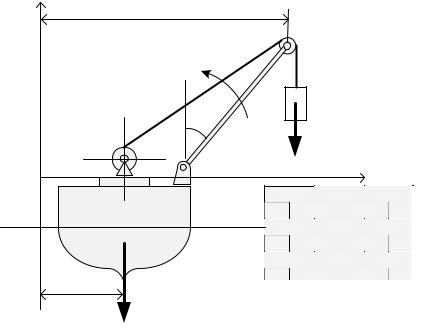
Определить перемещение S плавучего крана, поднимающего груз весом Р1=2т, при повороте стрелы крана на 300 до вертикального положения (рис.3.4).
Вес крана Р2=20т; длина стрелы l =8 м. Сопротивлением воды пренебречь. Решение:
Механическая система состоит из двух тел: плавучего крана и груза. Внешними силами, приложенными к системе являются вес крана Р1, вес груза Р2 и давление воды, направленное снизу вверх (на рисунке не показано). Все эти внешние силы вертикальны, поэтому сумма их проекций на горизонтальную ось равна нулю.
66
y |
x2 |
|
|
|
A |
|
30° |
|
P2 |
O |
x |
|
P
x1
1
Рис.3.4
В соответствии со следствием 2 из теоремы о движении центра масс делаем вы-
|
|
|
|
|
|
|
|
|
n |
вод: поскольку сумма проекций внешних сил на ось х равна нулю , то ∑ Fkxe = 0 , то |
|||||||||
|
= const. |
|
|
|
|
|
|
|
k =1 |
& |
|
|
|
|
|
|
|
|
|
xC |
Поскольку в начальном состоянии система покоится, то хс=const., |
||||||||
|
|
||||||||
|
Введем неподвижную систему координат Оxy (рис.3.4). |
||||||||
|
Запишем выражение для определения положения центра масс в начальном поло- |
||||||||
|
|
|
|
x m + x m |
x P + x P |
||||
жении системы: |
x = |
1 1 |
2 2 |
= |
1 1 |
2 2 |
. |
||
|
|
|
|
||||||
C |
m + m |
P + P |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
1 |
2 |
|
Запишем выражение для определения положения центра масс в конечном положении системы с учетом изменения начальных координат точек приложения сил Р1
|
|
x¢m + x¢m x¢P + x¢P |
( 1 |
+ S |
) 1 |
+ |
( 2 |
+ S -l ×sin 30° |
) |
2 |
|
|||||
и Р2: |
x = |
1 1 |
2 2 |
= |
1 1 |
2 2 |
= |
x |
P |
x |
|
P |
. |
|||
|
|
|
|
|
|
|
|
P + P |
|
|
||||||
C |
m + m |
P + P |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
1 |
2 |
|
|
|
|
|
1 |
2 |
|
|
|
Так как знаменатели в этих выражениях равны, то приравняем числители дробей:
x P + x P = ( x + S ) P + |
( x + S -l ×sin 30°) P , |
|
|
|
|||||||||
1 |
1 |
2 |
2 |
1 |
|
1 |
|
2 |
2 |
|
|
|
|
Упрощая полученное равенство, получим: |
(P + P ) S - P l ×sin 30° = 0. |
||||||||||||
1 |
2 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
Решая полученное уравнение относительно неизвестной переменной S, полу- |
|||||||||||
|
|
S = |
P l ×sin 30° |
= |
2×8×0.5 |
= 0.36(м). |
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
||||
чим |
|
( |
P + P |
|
22 |
|
|
|
|||||
|
|
|
1 2 ) |
|
|
|
|
|
|
|
|
||
Ответ: S = 0,36м
67
3.3 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
Производная по времени от количества движения механической системы равна
главному вектору внешних сил, действующих на систему: dQ = ∑n R e
dt k =1
Fk
dQ |
|
|
n |
||
|
|
x |
|
= ∑ Fkxe |
|
dt |
|
||||
|
|
|
k =1 |
||
dQ |
|
|
n |
||
или в проекциях на оси: |
|
|
y |
= ∑ Fkye . |
|
|
dt |
|
|||
|
|
|
k =1 |
||
dQ |
|
|
n |
||
|
|
z |
= ∑ Fkze |
||
|
|
||||
dt |
|
|
k =1 |
||
Количеством движения материальной точки называется векторная величина,
R |
|
R |
|
|
|
равная произведению массы точки на ее скорость: Q = mv . |
|
|
|
||
Количеством движения материальной системы называется |
геометрическая |
||||
R |
n |
R |
|
R |
R |
сумма количеств движения всех точек системы: Q = ∑ mr vr |
или |
Q = mvC . |
|||
r =1
Количество движения характеризует только поступательную часть движения и никакого отношения не имеет к его вращательной составляющей.
Следствие 1:
Если главный вектор внешних сил механической системы все время равен нулю, то вектор количества движения системы постоянен.
Следствие 2:
Если сумма проекций всех внешних сил механической системы на какую-либо ось все время равна нулю, то проекция количества движения на эту ось постоянна.
и
'5
Задача 3.7. Теорема об изменении количества движения
Механическая система состоит из двух материальных точек с массами •C 2 кг
•5 3кг, движущимися с взаимно перпендикулярными скоростями 'C 4 м и
с
2 м. Чему равно количество движения этой механической системы?
с
Решение:
Количество движения механической системы определяется по формуле:
¦ ∑> •¨'¨
¨QC .
68
m2v 2 |
Q |
|
|
|
m1v 1 |
|
Рис.3.5 |
Для двух материальных точек оно равно сумме двух векторов
которые |
можно |
сложить |
по |
правилу |
||
¦ "•C'C$5 "•5'5 |
$5 "2 ∙ 4$5 "3 ∙ 2$5 10" с |
$. |
||||
|
|
|
|
|
кг∙м |
|
Ответ: |
Q=10 кг·м/с. |
|
|
|
|
|
¦ •C'C •5'5 ,
параллелограмма:
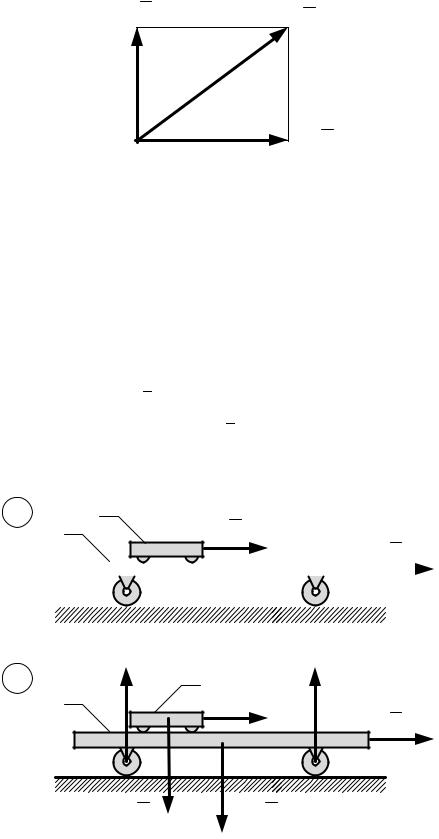
Задача 3.8. Теорема об изменении количества движения
Платформа массой •C 160 кг движется по гладкой горизонтальной плоскости с
постоянной скоростью '› 2.0 м. По платформе движется тележка массой •5
с
40 кг с относительной скоростью © 2.5 м. В некоторый момент времени тележка
с
была заторможена. Чему равна общая скорость платформы вместе с тележкой после остановки тележки?
2
а 1
u
v 0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N 1 2 |
|
|
|
|
|
|
|
||
б |
|
|
|
N 2 |
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
||||||||
|
|
|
|
|
|
|
|||||
v 0
m2 |
g |
m1 g |
Рис.3.6
69
Решение:
Применим теорему об изменении главного вектора количества движения систе- |
|
мы: |
ª¦⁄ª# ∑¨QC> «¨¬ , |
где ∑¨QC> |
«¨¬ - геометрическая сумма внешних сил, которая в случае данной зада- |
чи определяется как: ∑¨QC> «¨¬ -C -5 •C® •5®. |
|
Получается, что сумма проекций всех внешних сил механической системы на ось |
||
х все время равна нулю, поэтому |
ª¦¯⁄ª# ∑¨QC> «¨¯¬ |
0. |
Отсюда следует, что ¦¯ °±6:#. |
|
|
Если обозначить количество движения системы в начальный момент времени как |
||||||||||||
¦¯›, а количество движения системы в момент остановки тележки как |
¦¯C, то из |
|||||||||||
следует, что |
¦¯› |
¦¯C. |
|
|
|
|
|
|
||||
Выразим величины |
¦¯› и ¦¯C и составим соответствующее уравнение. |
|||||||||||
В начальный момент времени количество движения системы равно: |
|
|||||||||||
|
|
¦¯› |
•C'› •5'5 |
|
|
|
|
|
|
|||
где '› - скорость платформы, |
|
|
|
|
|
|
||||||
'5 |
- абсолютная скорость тележки, которая равна: |
|
||||||||||
'5 = '› © 2 2.5 4.5 " с $. |
|
|
|
|
|
|
||||||
|
|
|
|
|
м |
|
|
|
|
|
|
|
Тогда |
¦¯› 160 ∙ 2 40 ∙ 4.5 500 " |
с |
$. |
|
|
|
||||||
|
|
|
|
|
|
|
|
кг∙м |
|
|
|
|
В момент остановки тележки количество движения системы равно |
|
|||||||||||
где ' |
|
¦¯C |
"•C •5$' "160 40$' 200', |
|
||||||||
- общая скорость. |
500 200', решая которое |
|
||||||||||
Формируем уравнение ¦¯› ¦¯C: |
определяем, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
м |
|
|
что скорость платформы после остановки тележки равна ' 2.5 |
|
. |
|
|||||||||
с |
|
|||||||||||
Ответ: ' 2.5 |
с. |
|
|
|
|
|
|
|
|
|
||
|
|
|
м |
|
|
|
|
|
|
|
|
|
3.4 Теорема об изменении кинетической энергии в интегральной форме
Изменение кинетической энергии механической системы за некоторый промежу-
ток времени равно сумме работ всех действующих в системе сил:
² ²› ∑>¨QC ³¨
или, выделяя отдельно работы внешних и внутренних сил: